自已动手作图搞清楚AVL树
@
目录
一、背景
二叉树是一种常用的数据结构,更是实现众多算法的一把利器。(可参考《自己动手作图深入理解二叉树、满二叉树及完全二叉树》)
二分搜索树(Binary Search Tree)做为一种能实现快速定位查找的二叉树也得到了广泛应用(底层实现可参考《用一个图书库实例搞懂二分搜索树的底层原理》)。
1 二分搜索树是一颗二叉树
2 二分搜索树每个节点的左子树的值都小于该节点的值,每个节点右子树的值都大于该节点的值
3 任意一个节点的每棵子树都满足二分搜索树的定义
- 但二分搜索树也有其局限性:比如我们给定[1,2,3,4,5,6,7]这样的数据并按顺序构成的二分搜索树就褪化成了线性链表,二分搜索树极度偏向右侧,且深度达到7级,查找搜索的时间复杂度也从O(logn)褪化成了O(n).
![在这里插入图片描述]()
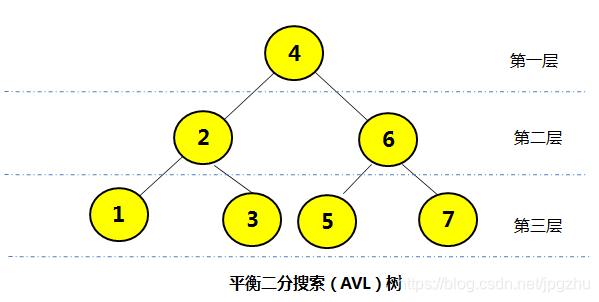
二、平衡二分搜索树---AVL树
- 为了解决二分搜索树的不平衡性,科学家创造一种自平衡的二分搜索树,这种树也被简称为AVL(G. M. Adelson-Velsky和E. M. Landis)树,以下的图即为一棵AVL树:
![在这里插入图片描述]()
2.1 AVL树的基本概念
每个结点的左右子树的高度之差(平衡因子)不大于1的二分搜索树,即为AVL树。
结点
- 结点是组成二叉树的最小单元。
-- 用图形表示
![在这里插入图片描述]()
-- 用代码表示
// 结点
class Node<E> {
E e;
Node left, right;
Node(E e) {
this.e= e;
this.left = null;
this.right = null;
}
}
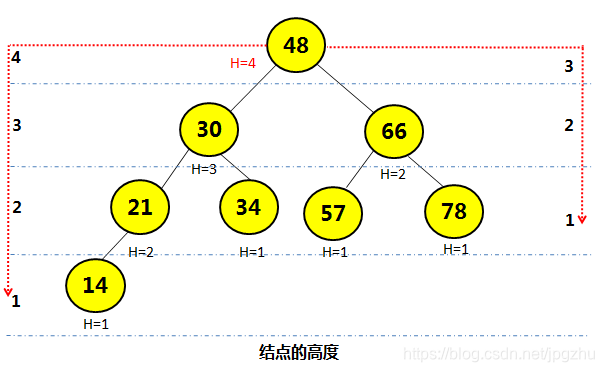
高度
- 叶子结点高度默认为1;非叶子结点的高度为该结点能到达的左子树或右子树的叶子结点的最大跨度。
![在这里插入图片描述]()
-- 用代码描述
class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
// 叶子结点高度默认为1
this.height = 1;
}
}
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算结点的高度
private void setHeight(Node node) {
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
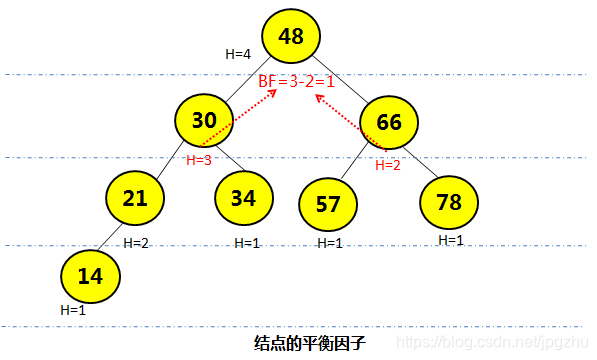
平衡因子
- 叶子结点的平衡因子为0;非叶子结点的平衡因子为该结点的左子结点或右子结点的高度差。
![在这里插入图片描述]()
-- 用代码描述
class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
// 叶子结点高度默认为1
this.height = 1;
}
}
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getHeight(node.left) - getHeight(node.right);
}
2.2 AVL树的验证
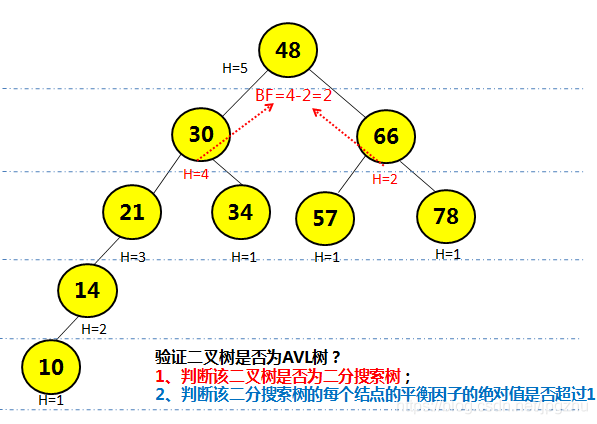
- 按AVL的定义,判断一棵二叉树是否为AVL树
- 首先需判断这棵二叉树是否为二分搜索树:即从根结点开始中序遍历该二叉树,形成的遍历序列一定是按从小到大有序排列的。
- 其实判断该二分搜索树的每个结点的平衡因子的绝对值是否超过1。
-- 用代码描述
/**
* AVL树
* @param <E> 泛型元素
* @author zhuhuix
* @date 2020-07-21
*/
public class AVL<E extends Comparable<E>> {
// 私有内部类-树结点
private class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
this.height = 1;
}
}
// 根结点
private Node root;
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算结点的高度
private int setHeight(Node node) {
return node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
// 增加元素
public void add(E e) {
root = addNode(root, e);
}
// 通过递归算法遍历现有结点,将新结点插入到合适的位置
private Node addNode(Node node, E element) {
if (node == null) {
System.out.println("新增元素[" + element + "] height=1");
return new Node(element);
}
// 新加入元素小于结点值,往左子树增加
if (element.compareTo((E) node.e) < 0) {
node.left = addNode(node.left, element);
// 新加入元素大于结点值,往右子树增加
} else if (element.compareTo((E) node.e) > 0) {
node.right = addNode(node.right, element);
} else // element.compareTo(node.e) == 0
{
node.e = element;
}
// 更新height
node.height = setHeight(node);
System.out.println("元素[" + node.e + "] 更新高度: height=" + node.height);
return node;
}
// 判断二叉树是否为二分搜索树:从根结点中序遍历形成的序列是否从小到大有序排列
public boolean isBST() {
ArrayList<E> arrayList = new ArrayList<>();
InOrderTraversal(root, arrayList);
for (int i = 0; i < arrayList.size() - 1; i++) {
// 相邻两个元素比较,如果前一个元素大于后一个元素,则不为二分搜索树
if (arrayList.get(i).compareTo(arrayList.get(i + 1)) > 0) {
return false;
}
}
System.out.println("中序遍历:" + arrayList.toString());
return true;
}
// 通过中序遍历形成序列
private void InOrderTraversal(Node node, ArrayList<E> arrayList) {
if (node == null) {
return;
}
InOrderTraversal(node.left, arrayList);
arrayList.add((E) node.e);
InOrderTraversal(node.right, arrayList);
}
// 判断是否是一棵平衡二叉树
public boolean isBalancedTree() {
return isBalanced(root);
}
// 通过递归遍历判断是否为平衡二叉树:判断每个结点的平衡因子的绝对值是否有大于1的存在
private boolean isBalanced(Node node) {
if (node == null) {
return true;
}
// 获取该结点的平衡因子,并判断平衡因子的绝对值是否大于1
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
System.out.println("元素["+node.e + "] 平衡因子=" + balanceFactor+",超过1");
System.out.println("元素["+node.e+ "] 左子树的高度="+node.left.height+ ",右子树的高度="+node.right.height);
return false;
}
// 遍历判断结点的左子树和右子树的各个结点
return isBalanced(node.left) && isBalanced(node.right);
}
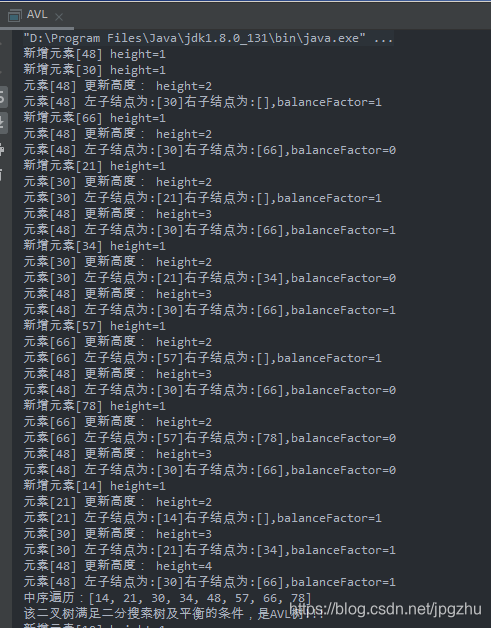
public static void main(String[] args) {
// 定义一个数组
Integer[] arr = {48, 30, 66, 21, 34, 57, 78, 14};
// 将该数组构建成一个二分搜索树
AVL<Integer> avl = new AVL<>();
for (int i = 0; i < arr.length; i++) {
avl.add(arr[i]);
}
// 判断当前的二叉树是否满足二分搜索树的定义
boolean isBST = avl.isBST();
boolean isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
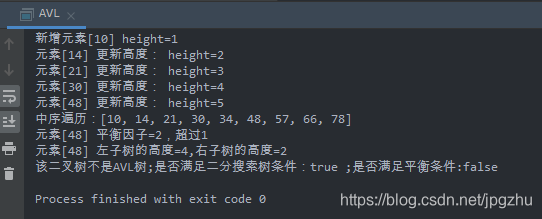
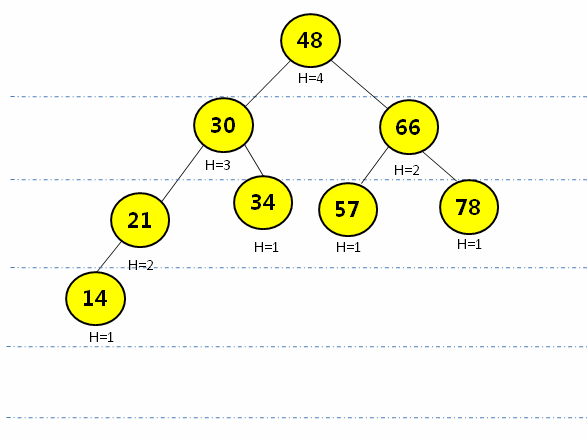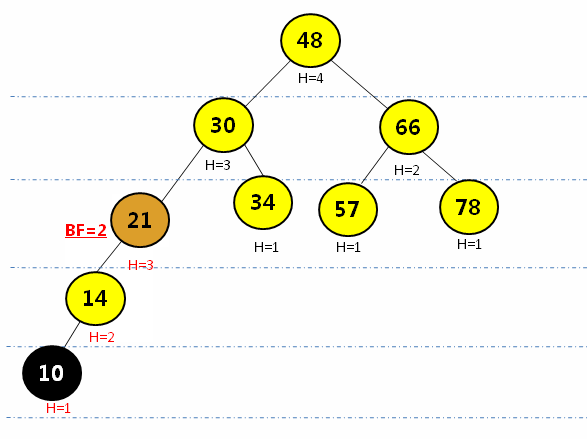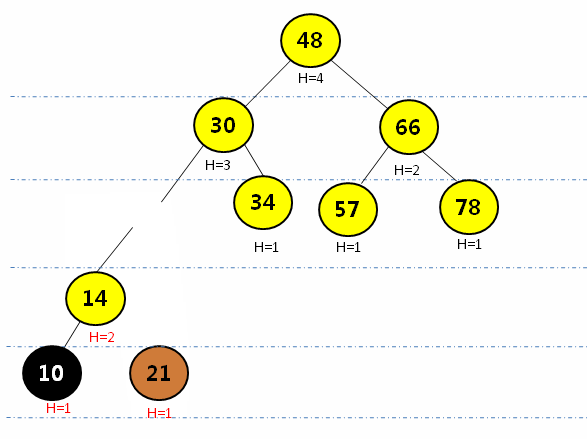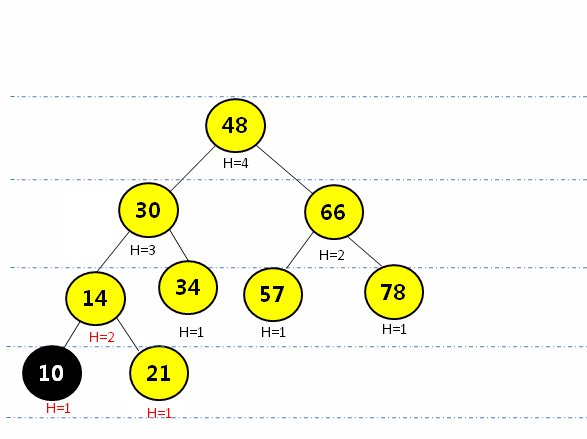
// 给该AVL树加上一个结点,再次判断是否判断
avl.add(10);
// 判断当前的二叉树是否满足二分搜索树的定义
isBST = avl.isBST();
isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
}
}
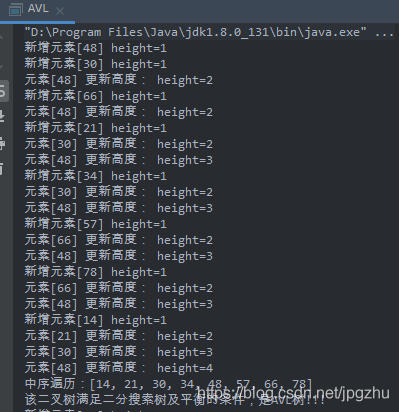
-
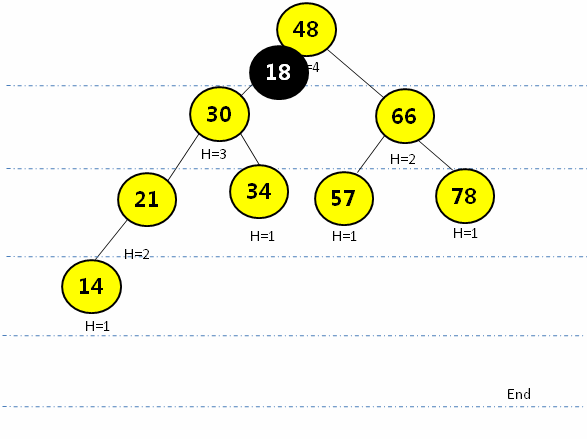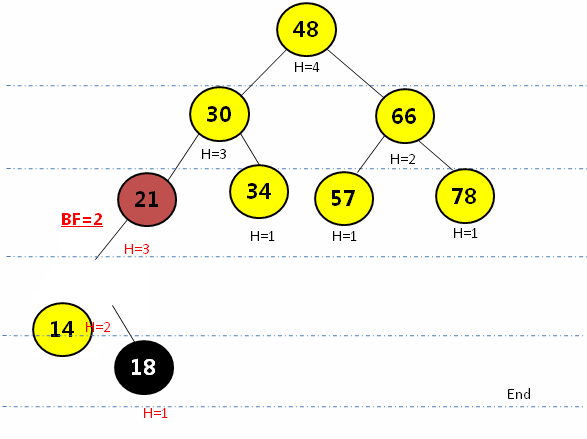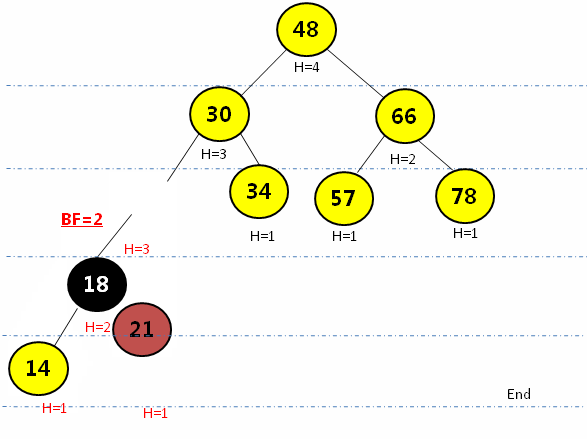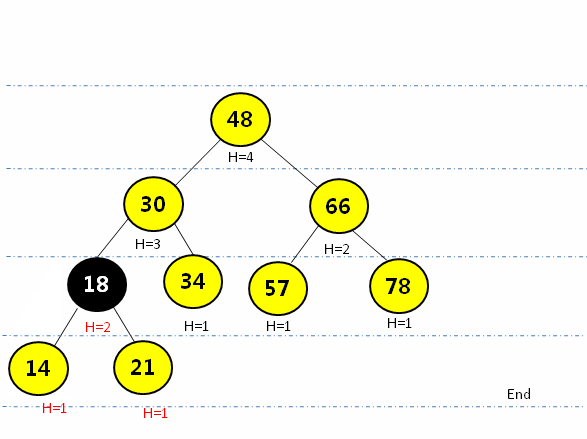
通过{48, 30, 66, 21, 34, 57, 78, 14}构建AVL树
![在这里插入图片描述]()
-
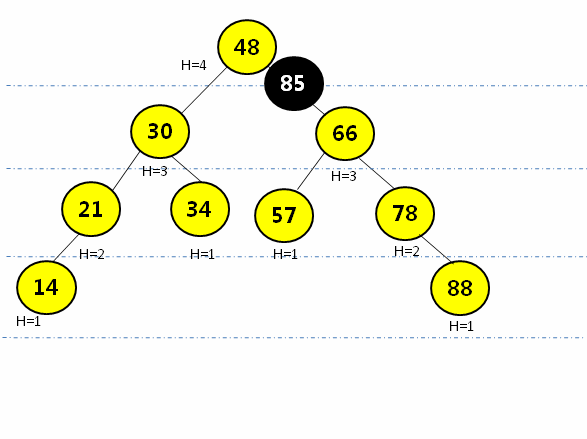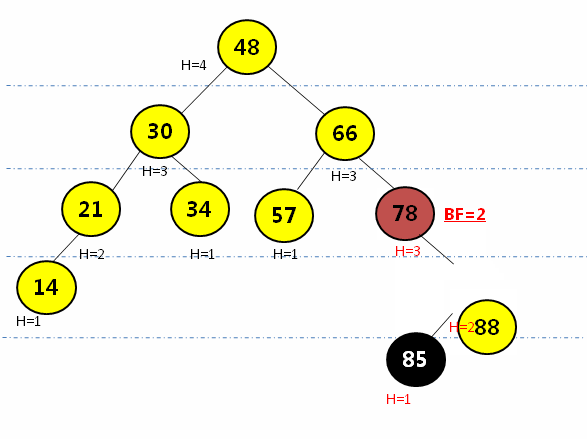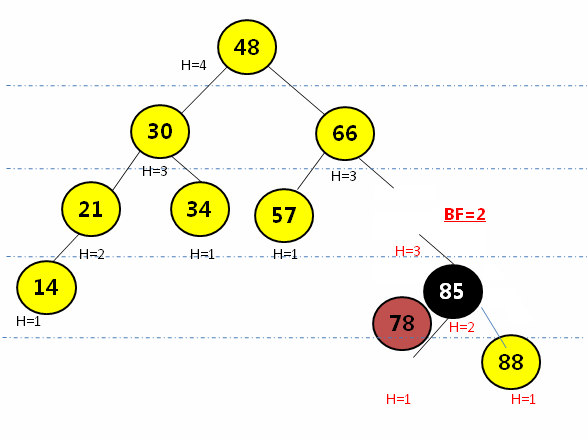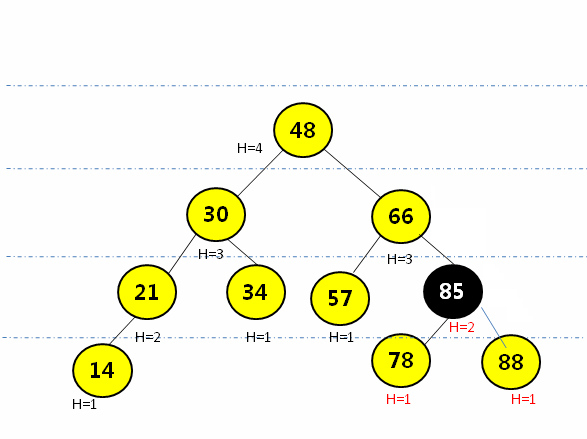
给以上AVL树增加一个结点10,再次判断该树是否满足AVL的定义
![在这里插入图片描述]()
三、旋转操作
往AVL树中添加结点很可能会导致失去平衡,所以我们需要在每次插入结点后进行平衡的维护。破坏平衡性有如下四种情况:
3.1 L L--需要通过右旋操作
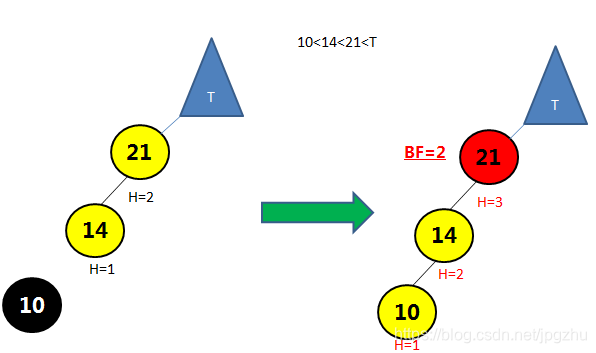
- 在结点的左子树(L)的左孩子(L)添加新的结点,会导致失去平衡:
![在这里插入图片描述]()
- 通过右旋操作(顺时针转)将平衡因子大于1的结点进行调整
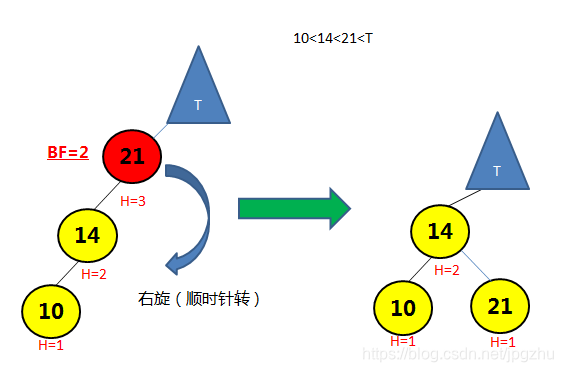
- 完整动画演示
![在这里插入图片描述]()
- 代码处理
// 右旋(顺时针转)
private Node rightRotate(Node y) {
Node x = y.left;
Node T = x.right;
// 向右旋转过程
x.right = y;
y.left = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 右旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
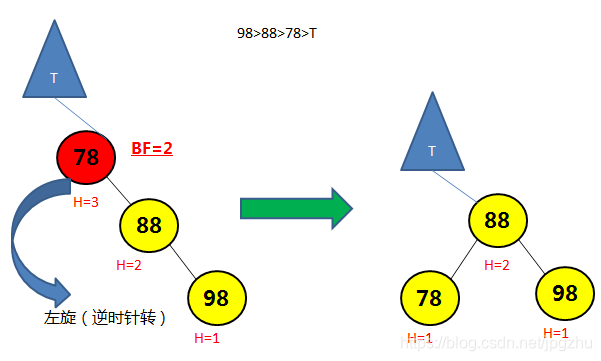
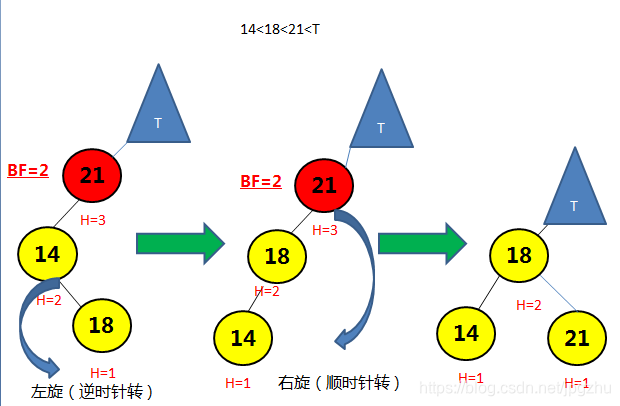
3.2 R R--需要通过左旋操作
- 在结点的右子树(R)的右孩子(R)添加新的结点,会导致失去平衡:
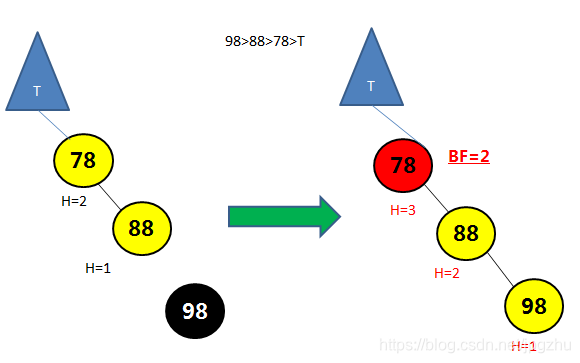
- 通过左旋操作(逆时针转)将平衡因子大于1的结点进行调整
![在这里插入图片描述]()
- 完整动画演示
![在这里插入图片描述]()
- 代码处理
// 左旋(逆时针转)
private Node leftRotate(Node y) {
Node x = y.right;
Node T = x.left;
// 向左旋转过程
x.left = y;
y.right = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 左旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
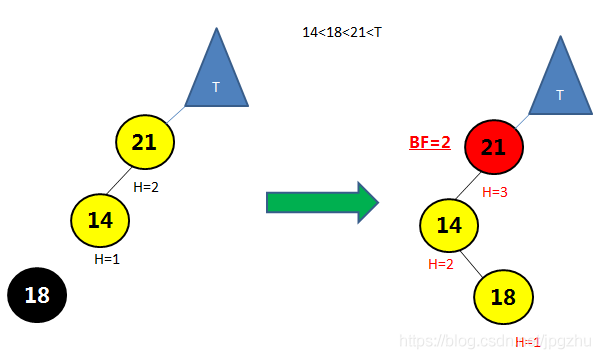
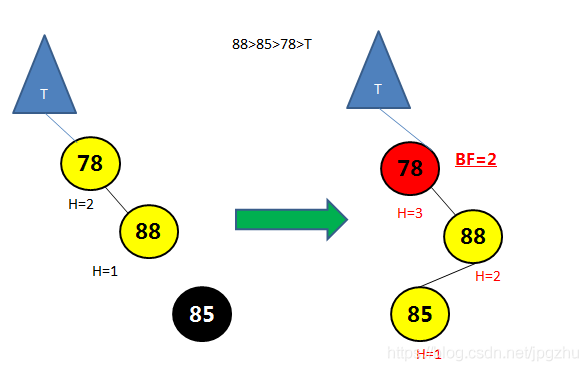
3.3 L R--需要先通过左旋再右旋操作
- 在结点的左子树(L)的右孩子(R)添加新的结点,会导致失去平衡:
![在这里插入图片描述]()
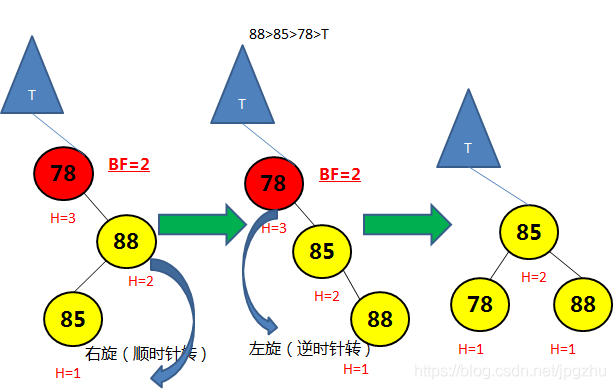
- 先通过左子结点的左旋操作(逆时针转)转成LL形式,再通过右旋操作(顺时针转)将平衡因子大于1的结点进行调整
![在这里插入图片描述]()
- 完整动画演示
![在这里插入图片描述]()
2.4 R L--需要先通过右旋再左旋操作
- 在结点的右子树(R)的左孩子(L)添加新的结点,会导致失去平衡:
![在这里插入图片描述]()
- 先通过右子结点的右旋操作(顺时针转)转成RR形式,再通过左旋操作(逆时针转)将平衡因子大于1的结点进行调整
![在这里插入图片描述]()
- 完整动画演示
![在这里插入图片描述]()
四、AVL树完整代码实现
/**
* AVL树
*
* @param <E> 元素
* @author zhuhuix
* @date 2020-07-21
*/
public class AVL<E extends Comparable<E>> {
// 私有内部类-树结点
private class Node<E> {
E e;
Node left, right;
// 高度
int height;
Node(E e) {
this.e = e;
this.left = null;
this.right = null;
this.height = 1;
}
}
// 根结点
private Node root;
// 获得节点node的高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
// 计算结点的高度
private int setHeight(Node node) {
return node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
// 获得节点node的平衡因子
private int getBalanceFactor(Node node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
// 右旋(顺时针转)
private Node rightRotate(Node y) {
Node x = y.left;
Node T = x.right;
// 向右旋转过程
x.right = y;
y.left = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 右旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
// 左旋(逆时针转)
private Node leftRotate(Node y) {
Node x = y.right;
Node T = x.left;
// 向左旋转过程
x.left = y;
y.right = T;
// 更新height
y.height = setHeight(y);
System.out.println("元素[" + y.e + "] 左旋后更新高度: height=" + y.height);
x.height = setHeight(x);
System.out.println("元素[" + x.e + "] 更新高度: height=" + x.height);
return x;
}
// 增加元素
public void add(E e) {
root = addNode(root, e);
}
// 通过递归算法遍历现有结点,将新结点插入到合适的位置
private Node addNode(Node node, E element) {
if (node == null) {
System.out.println("新增元素[" + element + "] height=1");
return new Node(element);
}
// 新加入元素小于结点值,往左子树增加
if (element.compareTo((E) node.e) < 0) {
node.left = addNode(node.left, element);
// 新加入元素大于结点值,往右子树增加
} else if (element.compareTo((E) node.e) > 0) {
node.right = addNode(node.right, element);
} else // element.compareTo(node.e) == 0
{
node.e = element;
}
// 更新height
node.height = setHeight(node);
System.out.println("元素[" + node.e + "] 更新高度: height=" + node.height);
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
if (node != null) {
System.out.println("元素[" + node.e + "] "
+ "左子结点为:[" + (node.left == null ? "" : node.left.e) + "]"
+ "右子结点为:[" + (node.right == null ? "" : node.right.e) + "]"
+ ",balanceFactor=" + balanceFactor);
}
// 平衡维护
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
System.out.println("元素[" + node.e + "] balanceFactor=" + balanceFactor + ",进行右旋");
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
System.out.println("元素[" + node.e + "] balanceFactor=" + balanceFactor + ",进行左旋");
return leftRotate(node);
}
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
System.out.print("元素[" + node.e + "] balanceFactor=" + balanceFactor + " 先将[" + node.e + "的左子结点" + node.left.e + "] 进行左旋");
node.left = leftRotate(node.left);
System.out.println("再将元素[" + node.e + "] 进行右旋");
return rightRotate(node);
}
if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
System.out.print("元素[" + node.e + "] balanceFactor=" + balanceFactor + " 先将[" + node.e + "的右子结点" + node.right.e + "] 进行右旋");
node.right = rightRotate(node.right);
System.out.println("再将元素[" + node.e + "] 进行左旋");
return leftRotate(node);
}
return node;
}
// 判断二叉树是否为二分搜索树:从根结点中序遍历形成的序列是否从小到大有序排列
public boolean isBST() {
ArrayList<E> arrayList = new ArrayList<>();
InOrderTraversal(root, arrayList);
for (int i = 0; i < arrayList.size() - 1; i++) {
// 相邻两个元素比较,如果前一个元素大于后一个元素,则不为二分搜索树
if (arrayList.get(i).compareTo(arrayList.get(i + 1)) > 0) {
return false;
}
}
System.out.println("中序遍历:" + arrayList.toString());
return true;
}
// 通过中序遍历形成序列
private void InOrderTraversal(Node node, ArrayList<E> arrayList) {
if (node == null) {
return;
}
InOrderTraversal(node.left, arrayList);
arrayList.add((E) node.e);
InOrderTraversal(node.right, arrayList);
}
// 前序遍历打印
public void preOrderTraversal() {
ArrayList<E> arrayList = new ArrayList<>();
preOrderTraversal(root, arrayList);
System.out.println("前序遍历" + arrayList);
}
// 通过前序遍历形成序列
private void preOrderTraversal(Node node, ArrayList<E> arrayList) {
if (node == null) {
return;
}
arrayList.add((E) node.e);
preOrderTraversal(node.left, arrayList);
preOrderTraversal(node.right, arrayList);
}
// 判断是否是一棵平衡二叉树
public boolean isBalancedTree() {
return isBalanced(root);
}
// 通过递归遍历判断是否为平衡二叉树:判断每个结点的平衡因子的绝对值是否有大于1的存在
private boolean isBalanced(Node node) {
if (node == null) {
return true;
}
// 获取该结点的平衡因子,并判断平衡因子的绝对值是否大于1
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
System.out.println("元素[" + node.e + "] 平衡因子=" + balanceFactor + ",超过1");
System.out.println("元素[" + node.e + "] 左子树的高度=" + node.left.height + ",右子树的高度=" + node.right.height);
return false;
}
// 遍历判断结点的左子树和右子树的各个结点
return isBalanced(node.left) && isBalanced(node.right);
}
public static void main(String[] args) {
// 定义一个数组
Integer[] arr = {48, 30, 66, 21, 34, 57, 78, 14};
// 将该数组构建成一个二分搜索树
AVL<Integer> avl = new AVL<>();
for (int i = 0; i < arr.length; i++) {
avl.add(arr[i]);
}
// 判断当前的二叉树是否满足二分搜索树的定义
boolean isBST = avl.isBST();
boolean isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
// 给该AVL树加上一个结点,再次判断是否判断
avl.add(10);
// 判断当前的二叉树是否满足二分搜索树的定义
isBST = avl.isBST();
isBalance = avl.isBalancedTree();
// 判断当前的树是否满足AVL定义
if (isBST && isBalance) {
System.out.println("该二叉树满足二分搜索树及平衡的条件,是AVL树!!!");
} else {
System.out.println("该二叉树不是AVL树;" + "是否满足二分搜索树条件:" + isBST + " ;是否满足平衡条件:" + isBalance);
}
}
}
- 构建AVL树过程
![在这里插入图片描述]()
- 添加结点AVL树平衡过程
![在这里插入图片描述]()






 浙公网安备 33010602011771号
浙公网安备 33010602011771号