【LeetCode 】N皇后II

【问题】n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

 

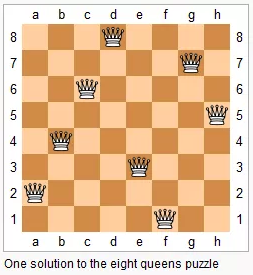
 上图为 8 皇后问题的一种解法。给定一个整数 n，返回 n 皇后不同的解决方案的数量。

示例:

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
[".Q..", // 解法 1
"…Q",
"Q…",
"..Q."],
["..Q.", // 解法 2
"Q…",
"…Q",
".Q.."]
]

【思路】回溯法继续

class Solution {
public:
    void solve(vector<bool>& cols_, vector<bool>& diag1s_, vector<bool>& diag2s_, int n, int row){
        if(row == n){
            count ++;
            return;
        }
        for(auto col = 0; col < n; col++){
            int ll = row + col;
            int rr = row - col + n - 1;
            if (cols_[col] && diag1s_[ll] && diag2s_[rr]){
                cols_[col] = false;
                diag1s_[ll] = false;
                diag2s_[rr] = false;

                solve(cols_, diag1s_, diag2s_, n, row+1);

                cols_[col] = true;
                diag1s_[ll] = true;
                diag2s_[rr] = true;
            }
        }
    }

    int totalNQueens(int n) {
        vector<bool> cols_(n, true);
        vector<bool> diag1s_(2*n-1, true);
        vector<bool> diag2s_(2*n-1, true);
        solve(cols_, diag1s_, diag2s_, n, 0);
        return count;
    }
private:
    int count = 0;
};