软件推荐-国内参数优化软件:1stOpt - First Optimizationg
首页:http://www.7d-soft.com/index.htm
4.0新功能 (预定2010年8月6日):
1:支持复数拟合、复数方程组计算;
2:支持微分方程拟合求解;
3:通用全局优化求解器变异功能,优化能力提高20%以上;
4:新的编程模式计算引擎;
5:强大易用的数据批处理拟合功能
6:公式自动搜索:增加更多的二维、三维函数库;
7:改进的积分计算,拟合,解方程可含有积分函数,支持高斯积分和辛普森积分算法
8:三维图形旋转、缩放、移动等功能
9:?号输入,可动态输入常数。
10:参数定义更加方便自由:Parameter 0<=a<=10, b=[1,3];
11:更多的数学函数支持:Wrap、Wrap0…
12:支持更多功能的关键字:FileWeight,OutWeight…
13:重复计算时自动记录每次结果
14:Exp函数计算修正,与Matlab等保持一致:Exp(-3^0.23)-> Exp(-(3^0.23))
15:….
3.0新功能 (2009年5月1日):
New in 3.0
1:重新设计的与其它高级语言的接口,更加方便与C++, Fortran, Basic, Pascal等语言的浑编联动。
2:增加新的算法:稳健全局优化算法。
3:改进了离子群和最大继承算法,优化能力更强。
4:增加了常微分方程(ODE)的求解功能,算法包括:龙格-库塔-费尔博格法(Runge-Kutta-Fehlberg Method)、欧拉算法(Euler
Method)、2-5阶龙格-库塔算法(Runge-Kutta Method),不仅能求解一般的初值ODE方程,还能解特殊形式的ODE方程,对边值问题的ODE方程也能轻松求解。
5:对线性规划问题自动判断识别,速度更快。
6:更加灵活的LoopConstant定义:LoopConstant d=[2,(max(x,1))];
7:与Vista兼容
8:编程模式增加对特殊函数的支持(Erf, Erfc, Gamma, Bessel…)
9:Parameter对For的支持。
10:拟合计算结束进行预测时,可计算每一点的导数
11:SubDivision、RunNext与Inherit功能
12:LogFile自动保存功能
13:RowData、RowDataSet与EndRowDataSet关键字
14:更加方便的Sum(),Prod()和For()语句
15:3D图形新格式:点状三维图
16:“恢复刚关闭的文件“功能
….
2.5新功能 (2006年10月7日):
1:更加出色、稳健的通用全局优化能力
1:对Basic的全面支持
2:参数型变量问题的拟合(未知中间变量):ParVariable
3:带积分的拟合和函数优化
4:隐函数优化算法的改进,速度增加10倍
5:隐函数拟合算法的订正:TradImplicit, ImplicitRange
6:BatchFile: 文件批处理功能
7:StepReg:逐步拟合功能
8:CodeSheet:代码本表格,支持直接从表格中读取数据
9:代码本显示形式:单业、多业和下拉
10:LoopConstant、FullLoopModel:自动循环计算功能
11:Constant a(1:3)=[1,2,3] -> Constant a = [1,2,3]
12:WeightReg:灵活多变、任意形式的带权重拟合
13:PassParameter:编程模式下支持返回计算变量
14:参数初值自动选择更加智能、健壮,适应范围更广
15:RegType:最小二乘法、最小一乘法等不同形式拟合
16:MDataSet,EndMDataset:网络节点数据自动转至矩阵数据
17:HotRun:设定自动热计算及计算次数
18:Sum,Prod,For更简洁写法
19:编程模式下可以直接定义二维参变量
20:Plot、PlotLoopData:迭代计算过程中更加丰富、强大的动态图形表示方式
21:众多改进及Bug修正
2.0新功能 (2006年10月7日):
1:求解非线性方程组功能大幅改进,【麦夸特法+通用全局优化算法】已成为解非线性方程组的首选算法,其改进后的求解能力总体上强于任何其它算法。
2:最大最小优化问题求解 (MinMax):一种多目标优化求解功能。
3:智能拟合功能:该功能特别适合于数据量很大时的拟合,可数倍甚至数十倍缩短计算时间,数据量越大,效果越明显。
4:改进的非常容易实现的带等式或不等式约束的拟合
5:算法自动选择功能:对于刚接触1stOpt的用户而言,由于不清楚各算法的特点及适用范围,常无法确定如何选择算法,该功能可根据问题的类型自动选择算法。
6:函数表达式以脚本语言描述表达功能:对于复杂、繁琐、冗长的问题,可通过脚本语言来描述
7:常字符串数组表达功能:定义字符串数组功能
例:ConstStr S(1:3) = [x1^2+x2, x1*x2-x2^2, sin(x1)+x2];
等同于:ConstStr S1 = x1^2+x2, S2 = x1*x2-x2^2, S3 = sin(x1)+x2;
例:ConstStr S(1:3) = x2*[x1^2+x2, x1*x2-x2^2, sin(x1)+x2];
等同于:ConstStr S1 = x2*(x1^2+x2), S2 = x2*(x1*x2-x2^2), S3 = x2*(sin(x1)+x2);
8:公式拟合自动搜索时稳健模式搜索功能
9:0-1规划,修正数值范围溢出问题
10:公式自动拟合库中,增加众多峰函数
11:约束函数连续表达功能:
例:10.3>=x1+sin(x2)*x3>=0
等同于:
x1+sin(x2)*x3>=0;
x1+sin(x2)*x3<=10.3;
例:Parameter x1[0.5,0.66], x4[0.04,0.2], x7[,0.035];
MinFunction 0.44*x1+0.94*x2+0.88*x3+0.48*x4+4*x5+3.4*x6+2.3*x7+0.12*x8+1.6*x9+19*x10+25*x11;
3230*x1+2640*x2+2500*x3+1730*x4+2900*x5+2230*x6+2500*x7>2750;
8.27*x1+43*x2+40*x3+15.4*x4+62*x5+50*x6+45*x7>15;
8.27*x1+43*x2+40*x3+15.4*x4+62*x5+50*x6+45*x7<16;
0.038*x1+0.32*x2+0.32*x3+0.14*x4+3.91*x5+4.6*x6+33.4*x8+21*x9>2.85;
0.038*x1+0.32*x2+0.32*x3+0.14*x4+3.91*x5+4.6*x6+33.4*x8+21*x9<3;
0.058*x1+0.15*x2+0.14*x3+0.32*x4+2.9*x5+2.15*x6+0.14*x8+18.5*x9>0.5;
0.058*x1+0.15*x2+0.14*x3+0.32*x4+2.9*x5+2.15*x6+0.14*x8+18.5*x9<0.55;
0.26*x1+2.45*x2+2.41*x3+0.54*x4+4.35*x5+3.28*x6+2.6*x7+99*x11>0.8;
0.125*x1+0.48*x2+0.51*x3+0.18*x4+1.65*x5+1.31*x6+0.65*x7+99*x10>0.31;
0.298*x1+1.08*x2+1.4*x3+0.58*x4+2.21*x5+1.74*x6+0.83*x7+99*x10>0.58;
0.298*x1+1.08*x2+1.4*x3+0.58*x4+2.21*x5+1.74*x6+0.83*x7+99*x10<0.63;
0.077*x1+0.6*x2+0.6*x3+0.27*x4+0.8*x5+0.64*x6>0.19;
x2+x3>0.1;
x2+x3<0.22;
x5+x6>0.03;
x5+x6<0.07;
x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11=1;
可写为:
Parameter x1[0.5,0.66], x4[0.04,0.2],x7[,0.035];
MinFunction 0.44*x1+0.94*x2+0.88*x3+0.48*x4+4*x5+3.4*x6+2.3*x7+0.12*x8+1.6*x9+19*x10+25*x11;
3230*x1+2640*x2+2500*x3+1730*x4+2900*x5+2230*x6+2500*x7>2750;
16>8.27*x1+43*x2+40*x3+15.4*x4+62*x5+50*x6+45*x7>15;
3>0.038*x1+0.32*x2+0.32*x3+0.14*x4+3.91*x5+4.6*x6+33.4*x8+21*x9>2.85;
0.55>0.058*x1+0.15*x2+0.14*x3+0.32*x4+2.9*x5+2.15*x6+0.14*x8+18.5*x9>0.5;
0.26*x1+2.45*x2+2.41*x3+0.54*x4+4.35*x5+3.28*x6+2.6*x7+99*x11>0.8;
0.125*x1+0.48*x2+0.51*x3+0.18*x4+1.65*x5+1.31*x6+0.65*x7+99*x10>0.31;
0.63>0.298*x1+1.08*x2+1.4*x3+0.58*x4+2.21*x5+1.74*x6+0.83*x7+99*x10>0.58;
0.077*x1+0.6*x2+0.6*x3+0.27*x4+0.8*x5+0.64*x6>0.19;
0.22>x2+x3>0.1;
0.07>x5+x6>0.03;
x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11=1;
12:矩阵计算,基本函数求导计算
13:带权重的拟合功能
14:带约束的超越方程求解
15:For语句,支持循环表达式
16:支持自动重复计算
17:改进的预测/验证功能
18:DataSet,AutoData定义数据时,可指定起始基数:
缺省时,起始基数为1
例:
DataSet;
EndDataSet:
例:AutoData x = 1:1:10;
例:定义起始基数为0
DataSet [Base = 0];
EndDataSet:
例:AutoData[Base = 0] x = 1:1:10;
19:增加IFF关键字
20:代码中直接从Excel表单和1stOpt电子表格中读取数据:必须指定文件名、表单名及数据范围
例:从Excel文件“C:\Data1.xls”中的“Sheet1”中读取数据进行拟合计算,数据范围从A1到B20
Function y = a + b*x + Exp(c*x);
DataFile C:\Data1.xls[Sheet1[A1:B20]];
21:常数连续定义:
例:Constant A(1:3) = 2;
等同于 Constant A1 = 2, A2 = 2, A3 = 2;
例:Constant A(1:3) = 10*[1,2,3];
等同于 Constant A(1:3) = [10,20,30];
22:增强的编程模式,可完善自动处理任意多的等式及不等式约束,对于复杂的带约束的工程问题,可轻易求解。
23:修正定义多维常数、参数时出现的问题
1.5新功能 (2006年4月18日):
1:单纯形线性规划算法中,可进行整数规划、混合整数规划计算。
2:编程模式中,对约束条件的自动处理功能。
3: 权重拟合功能
4:结果数据自动保存功能。
5:同一代码本中,所有问题同时求解功能。
6:函数优化预测检验功能
7:数据自动产生功能: 关键字: AutoData
例:AutoData X = 1:1:10, Y = X^2+X;
等同于:Constant X(1:10) = [1,2,3,4,5,6,7,8,9,10];
Constant Y(1:10) = [2,6,12,20,30,42,56,72,90,110];
8: 循环语句关键字:For,支持无穷镶套
例:For(i=1:3)(x[i]>=A[i]*i);
等同于: x[1] >=A[1]*1;
x[2] >=A[2]*2;
x[3] >=A[3]*3;
9: 新增特殊密度分布函数:BetaCDF, BetaPDF, BinoCDF, BinoPDF, Chi2CDF, Chi2PDF, ExpCDF,
ExpPDF, PoissCDF, PoissPDF, TCDF, TPDF
10:增加函数求导计算功能
例:(x*exp(x+sin(x)))’ ==>
diff(x*exp(x+sin(x)),x) = exp(x+sin(x))+exp(x+sin(x))*(1+cos(x))*x
diff(x*exp(x+sin(x)),x=3) = exp(x+sin(x))+exp(x+sin(x))*(1+cos(x))*x = 23.82417126
11:新增:
BinParameter: 定义0-1变量;
IntParameter: 定义正整数变量;
ParameterDomain:定义变量范围;
PlotXYZData:画三维数据图;
PlotMeshData:画三维网格数据图;
PlotPoint3D:画三维点图;
12:众多改进,运行更快捷、稳定。
错误纠正:
1:函数表达式中出现空格显错的问题。
2:拟合时,用“DataFile”调用外部数据文件出错。
3:用超过两次“DataSet- EndDataSet”定义数据时出错
4:拟合时,用“SkipStep“出错。
5:函数中出现诸如“2E+10“时显错的问题。
6: 其它诸多Bugs

1 //There are many test examples located in the folder: examples\ 2 3 //Nonlinear regression: any No. of variables and parameters, any user-defined function 4 Title "NLReg Demo - 1"; 5 Parameter b1, b2, b3, b4; 6 Variable x, y; 7 Function y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x); 8 Data; 9 //x y 10 2 4 11 2.1 4.1 12 2.2 4.3 13 2.3 4.5 14 2.4 4.6 15 2.5 4.8 16 2.6 5.0 17 2.7 5.1 18 2.8 5.3 19 2.9 5.5 20 21 NewDivision "NLReg Demo - 2"; 22 //Data may be in codesheet, the simplified formation is like below: 23 Function y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x); 24 DataFile "CodeSheet1[A2:B11]"; //Press F2 to view data 25 26 NewDivision "NLReg Demo - 3"; 27 //The data may be in row type: 28 Function y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x); 29 RowData; 30 2,2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9; 31 4,4.1,4.3,4.5,4.6,4.8,5.0,5.1,5.3,5.5; 32 33 NewDivision "NLReg Demo - 4"; 34 //In program model (Pascal): 35 Variable x, y; 36 Parameter b(4); 37 StartProgram [Pascal]; 38 Procedure MainModel; 39 var i: integer; 40 Begin 41 for i := 0 to DataLength - 1 do 42 y[i] := exp(b1*x[i])+exp(b2*x[i])+b3*sin(b4*x[i]); 43 End; 44 EndProgram; 45 RowData; 46 2,2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9; 47 4,4.1,4.3,4.5,4.6,4.8,5.0,5.1,5.3,5.5; 48 49 NewDivision "NLReg Demo - 5"; 50 //In program model (Basic): 51 Variable x, y; 52 Parameter b(4); 53 StartProgram [Basic]; 54 Sub MainModel 55 Dim i as integer 56 for i = 0 to DataLength - 1 57 y(i) = exp(b1*x(i))+exp(b2*x(i))+b3*sin(b4*x(i)) 58 Next 59 ConstrainedResult = b1+b2+b3=1 60 End Sub 61 EndProgram; 62 DataFile "CodeSheet1[A2:B11]"; //Press F2 to view data 63 64 NewDivision "NLReg Demo - 6"; 65 //Constrained regression: b1, b2, b3 >=0; b1+b2+b3=1; 66 Parameter b(3) =[0,]; 67 Function y=exp(b1*x)+exp(b2*x)+b3*sin(b4*x); 68 b1+b2+b3=1; 69 DataFile "CodeSheet1[A2:B11]"; //Press F2 to view data 70 71 NewDivision "NLReg Demo - 7"; 72 //parameters are shared by various function 73 SharedModel; 74 Variable x,y1,y2; 75 Function y1=a+g*t^2*x^2/(1+t^2*x^2)+c*x^d; 76 y2=b+g*t*x/(1+t^2*x^2)+c*x^d1; 77 DataFile "CodeSheet1[C2:E23]"; //Press F2 to view data 78 79 NewDivision "NLReg Demo 8"; 80 //curve fitting with integration 81 Variables x, y; 82 Parameters a, b, c, d; 83 Function y=a-b*exp(-c*x^d)*int((t+x)*sin(x),t=0.1:c); 84 data; 85 0.05 0.13 86 0.15 0.13 87 0.25 0.19 88 0.35 0.34 89 0.45 0.53 90 0.55 0.71 91 0.65 1.06 92 0.75 1.6 93 0.85 1.64 94 0.95 1.83 95 1.05 2.09 96 1.15 2.05 97 1.25 2.13 98 1.35 2.12 99 1.45 2.09 100 101 NewDivision "NLReg Demo 9"; 102 {Two times of x-y data with different T, k1, k2, k3, k4 are parameters, 103 regression equation: y=k1*k3*exp((k2+k4)/T)*x/(1+k3*exp(k4/T)*x) 104 105 Data: 106 T= 288K T=303K 107 x y x y 108 0 0 0 0 109 3.41586 0.04887 8.31345 0.0901 110 9.47655 0.13519 28.43464 0.26128 111 24.02448 0.29356 59.3231 0.4764 112 56.42759 0.51347 94.48793 0.66564 113 93.07483 0.7103 135.639 0.836 114 132.8176 0.8863 179.1531 0.97904 115 172.8579 1.03949 218.6459 1.0981 116 210.2345 1.16252 254.779 1.18808 117 238.6986 1.27173 283.5697 1.25296 118 272.3641 1.35695 308.7593 1.30915 119 297.1748 1.42801 120 313.8014 1.48757 121 122 How to estimate paremeters of k? } 123 Variable x,y; 124 Parameter k(4); 125 VarConstant t=[288,303]; 126 StartProgram [Pascal]; 127 Procedure MainModel; 128 var j: integer; 129 Begin 130 for j := 0 to DataLength -1 do 131 y[j] := k1*k3*exp((k2+k4)/T)*x[j]/(1+k3*exp(k4/T)*x[j]); 132 133 End; 134 EndProgram; 135 Data; 136 //x y 137 0 0 138 3.41586 0.04887 139 9.47655 0.13519 140 24.02448 0.29356 141 56.42759 0.51347 142 93.07483 0.7103 143 132.8176 0.8863 144 172.8579 1.03949 145 210.2345 1.16252 146 238.6986 1.27173 147 272.3641 1.35695 148 297.1748 1.42801 149 313.8014 1.48757 150 Data; 151 //x y 152 0 0 153 8.31345 0.0901 154 28.43464 0.26128 155 59.3231 0.4764 156 94.48793 0.66564 157 135.639 0.836 158 179.1531 0.97904 159 218.6459 1.0981 160 254.779 1.18808 161 283.5697 1.25296 162 308.7593 1.30915 163 164 NewDivision "NLReg Demo 10"; 165 Function y=c*(1+Erf(((x-b)*exp(-a*(x/b)))/(sqrt(2)*a*b))); 166 Data; 167 0 0 168 50 0 169 100 0 170 150 0 171 200 0 172 250 0 173 300 0 174 350 0 175 400 0 176 450 0.04 177 500 0.08 178 550 0.14104 179 600 0.18635 180 650 0.24 181 700 0.3 182 750 0.38272 183 800 0.44474 184 850 0.5573 185 900 0.64532 186 950 0.69053 187 1000 0.76975 188 1050 0.82394 189 1100 0.86369 190 1150 0.90259 191 1200 0.93255 192 1250 0.96256 193 1300 0.98994 194 1350 0.99023 195 1400 0.99621 196 1450 0.99821 197 1500 1 198 1550 1 199 1600 1 200 201 NewDivision "NLReg Demo 11"; 202 Parameter a,b,c,d; 203 Function y = (A-D)/(1+(x/C)^B) + D; 204 Data; 205 0.01953125 0.624 206 0.078125 0.728 207 0.15625 0.827 208 0.3125 0.976 209 0.390625 1.138 210 0.625 1.243 211 2.5 1.292 212 5 1.414 213 10 1.496 214 215 NewDivision "Equation Solve - 1"; 216 Function x*0.090949*0.274666*(1 - y*Exp(-4*z)) - a = 0.00097; 217 x*0.206949*0.274666*(1 - y*Exp(-40*z)) - a = 0.00681; 218 x*0.230149*0.274666*(1 - y*Exp(-46*z)) - a = 0.00785; 219 x*0.241749*0.274666*(1 - y*Exp(-109*z)) - a = 0.01131; 220 221 NewDivision "Equation Solve - 2"; 222 Constant R=50,D=10,bta=0.75,p=10e6; 223 Parameter x,y,m,n; 224 Function 225 p+2*bta*R^3*x/(3*R+2*D-m)^3+2*bta*R^3*x/(3*R+2*D-m)^3+2*bta*R^3*y/(R+D-n)^3=R^3*y/(R-n)^3; 226 p+2*bta*R^3*x/(5*R+2*D-m)^3+2*bta*R^3*x/(R+D-m)^3+2*bta*R^3*y/(3*R+D-m)^3=R^3*y/(R+n)^3; 227 p+2*bta*R^3*x/(5*R+3*D-m)^3+2*bta*R^3*y/(3*R+2*D-n)^3+2*bta*R^3*y/(R+D+n)^3=R^3*x/(R-m)^3; 228 p+2*bta*R^3*x/(7*R+3*D-m)^3+2*bta*R^3*y/(5*R+2*D-n)^3+2*bta*R^3*y/(3*R+D+n)^3=R^3*x/(R+m)^3; 229 230 NewDivision "Equation Solve - 3"; 231 {System equations: 232 1-2*cos(a1)+2*cos(a2)-2*cos(a3)+2*cos(a4)-2*cos(a5)+2*cos(a6)=1.60; 233 1-2*cos(5*a1)+2*cos(5*a2)-2*cos(5*a3)+2*cos(5*a4)-2*cos(5*a5)+2*cos(5*a6)=0; 234 1-2*cos(7*a1)+2*cos(7*a2)-2*cos(7*a3)+2*cos(7*a4)-2*cos(7*a5)+2*cos(7*a6)=0; 235 1-2*cos(11*a1)+2*cos(11*a2)-2*cos(11*a3)+2*cos(11*a4)-2*cos(11*a5)+2*cos(11*a6)=0; 236 1-2*cos(13*a1)+2*cos(13*a2)-2*cos(13*a3)+2*cos(13*a4)-2*cos(13*a5)+2*cos(13*a6)=0; 237 1-2*cos(17*a1)+2*cos(17*a2)-2*cos(17*a3)+2*cos(17*a4)-2*cos(17*a5)+2*cos(17*a6)=0;} 238 ParameterDomain = [0,pi/2]; 239 Constant p=[1,5,7,11,13,17], v=[1.6,0,0,0,0,0]; 240 Function For(i=1:6,p,v)(1-2*cos(p*a1)+2*cos(p*a2)-2*cos(p*a3)+2*cos(p*a4)-2*cos(p*a5)+2*cos(p*a6)=v); 241 242 NewDivision "ODE Function"; 243 Variable t = [0,3], y=1, z=1; 244 Plot y[x], z; 245 ODEOptions = [SN=200,A=0,P=30]; 246 ODEFunction y' = cos(z'-y')*t*y/(1+z); 247 z' = (t*z+y*exp(y)*sin(y'))/2; 248 249 NewDivision "Function Optimization - 1"; 250 MinFunction Ba; 251 Ba*SO4=1; 252 BaOH/Ba*OH=4.8; 253 HSO4/SO4*H=0.98; 254 H*OH=1; 255 Ba+10^(-7)*BaOH=SO4+10^(-5)*HSO4; 256 2*Ba+1E-7*BaOH+1E-2H=2*SO4+1E-5*HSO4+1E-2*OH; 257 258 NewDivision "Rosenbrok function"; 259 Constant n=4; 260 Parameters x(1:n+1)[-1.5,1.5]; 261 Minimum = true; 262 Function sum(i=1:n)(100*(x[i+1]-x[i]^2)^2+(1-x[i])^2); 263 264 NewDivision "Ackley function 2 - Optimization"; 265 Constant n = 4; 266 Parameters x(1:n)[-30,30]; 267 Minimum = true; 268 Function sum(i=1:n-1)(3*(cos(2*x[i])+sin(2*x[i+1]))+sqrt(x[i+1]^2+x[i]^2)); 269 270 NewDivision "NLReg Demo 12"; 271 //nonlinear regression with multi-files 272 Variable t,h; 273 Parameter a, a1, k, k1; 274 VarConstant b=[2,4,6,8]; 275 StartProgram [Pascal]; 276 Procedure MainModel; 277 var i: integer; 278 temb, h0: double; 279 Begin 280 temb := b; 281 h0 := 0; 282 for i := 0 to DataLength -1 do begin 283 h0 := h0+ a*(temb-a1*tanh(k1*h0))*exp(k*(temb-a1*tanh(k1*h0)))*250; 284 h[i] := h0; 285 end; 286 End; 287 EndProgram; 288 Data; 289 //0 0 290 250 0.226066238 291 500 0.281510409 292 750 0.314326458 293 1000 0.351110333 294 1250 0.375454391 295 1500 0.398296935 296 1750 0.417922218 297 2000 0.435617147 298 2250 0.451381719 299 Data; 300 //0 0 301 250 0.5653775 302 500 0.8946725 303 750 1.1468305 304 1000 1.3735105 305 1250 1.5691755 306 1500 1.7503255 307 1750 1.9100265 308 2000 2.0534495 309 2250 2.1794185 310 Data; 311 //0 0 312 250 1.760498 313 500 2.784063 314 750 3.657308 315 1000 4.438827 316 1250 5.171771 317 1500 5.860787 318 1750 6.513054 319 2000 7.140139 320 2250 7.746008 321 Data; 322 //0 0 323 250 4.03011 324 500 6.880921 325 750 9.285056 326 1000 11.364176 327 1250 13.288876 328 1500 14.892276 329 1750 16.389606 330 2000 17.784386 331 2250 19.036266 332 333 NewDivision "ODE Regression"; 334 //Eurle method 335 //x'=dx/dt=p1*(20-x)+p2*(p3-x); 336 //y'=dy/dt=p1*(x-y)+p2*(p3-y) 337 //z'=dz/dt=p1*(y-z)+p2*(p3-z) 338 Constant V = [10,15,20]; //Initial Values 339 Constant dt=1; 340 Parameter p(3);//=[0.5,100]; 341 Variable t, x[OutPut], y[OutPut], z[OutPut]; 342 StartProgram [Pascal]; 343 Procedure MainModel; 344 var i: integer; 345 x0,y0,z0: double; 346 Begin 347 x0 := V[1]; 348 y0 := V[2]; 349 z0 := V[3]; 350 for i := 0 to DataLength - 1 do begin 351 x0 := (p1*(20-x0)+p2*(p3-x0))*dt+x0; 352 y0 := (p1*(x0-y0)+p2*(p3-y0))*dt+y0; 353 z0 := (p1*(y0-z0)+p2*(p3-z0))*dt+z0; 354 x[i] := x0; 355 y[i] := y0; 356 z[i] := z0; 357 end; 358 End; 359 EndProgram; 360 Data; 361 //0 10 15 20 362 1 11.80 15.37 20.77 363 2 14.04 17.04 22.23 364 3 15.44 16.85 21.16 365 4 17.80 18.07 22.49 366 5 18.60 19.43 24.46 367 6 19.22 20.12 23.58 368 7 21.77 21.83 24.51 369 8 22.17 22.11 25.38 370 9 23.41 23.37 25.53 371 10 23.17 24.92 26.69 372 11 24.56 25.55 29.21 373 12 25.85 26.06 28.00 374 13 24.64 28.94 30.32 375 14 25.15 28.94 30.41 376 15 26.92 30.06 31.87 377 16 26.37 29.29 31.87 378 17 26.71 31.48 34.60 379 18 26.61 31.86 33.57 380 19 27.13 33.84 36.75 381 20 29.32 32.95 36.36 382 21 28.24 33.03 36.23 383 22 28.42 32.50 36.01 384 23 28.11 33.12 39.19 385 24 28.98 35.32 37.29 386 25 30.23 35.56 37.79 387 26 30.21 34.86 42.05 388 27 29.11 35.40 42.67 389 28 30.42 36.20 40.74 390 29 28.84 35.91 40.53 391 30 29.44 36.50 43.33 392 393 NewDivision "ODE Regression"; 394 //4th-order RK 395 Constant y1_1=10, y2_1=15, y3_1=20; //Initial Values 396 Constant m=3, dx=1; //m: function number 397 Parameter p(3);//=[0.5,100]; 398 Variable t, x[OutPut], y[OutPut], z[OutPut]; 399 Minimum; 400 StartProgram [Pascal]; 401 Procedure MainModel; 402 var i, j: integer; 403 y1_2, y2_2, y3_2: double; 404 y11, y21, y31: double; 405 rk1, rk2, rk3, rk4, y_y, yy, dydx: array[0..m-1] of double; 406 x, tx: double; 407 Procedure Drive(x_d: double; y_d: array of double; var dydx_d: array of double); 408 begin 409 dydx_d[0] := p1*(20-y_d[0])+p2*(p3-y_d[0]); 410 dydx_d[1] := p1*(y_d[0]-y_d[1])+p2*(p3-y_d[1]); 411 dydx_d[2] := p1*(y_d[1]-y_d[2])+p2*(p3-y_d[2]); 412 end; 413 begin 414 yy[0]:=y1_1; 415 yy[1]:=y2_1; 416 yy[2]:=y3_1; 417 y_y[0]:=y1_1; 418 y_y[1]:=y2_1; 419 y_y[2]:=y3_1; 420 for i := 0 to DataLength-1 do begin 421 for j := 0 to m-1 do y_y[j] := yy[j]; 422 tx := dx*i; 423 x := tx; 424 Drive(x, yy, dydx); 425 for j := 0 to m-1 do rk1[j] := dydx[j]; 426 x := tx+0.5*dx; 427 for j := 0 to m-1 do 428 yy[j] := y_y[j] + 0.5*rk1[j]*dx; 429 Drive(x, yy, dydx); 430 for j := 0 to m-1 do 431 rk2[j] := dydx[j]; 432 x := tx+0.5*dx; 433 for j := 0 to m-1 do 434 yy[j] := y_y[j] + 0.5*rk2[j]*dx; 435 Drive(x, yy, dydx); 436 for j := 0 to m-1 do 437 rk3[j] := dydx[j]; 438 x := tx+dx; 439 for j := 0 to m-1 do 440 yy[j] := y_y[j] + rk3[j]*dx; 441 Drive(x, yy, dydx); 442 for j := 0 to m-1 do 443 rk4[j] := dydx[j]; 444 for j := 0 to m-1 do 445 yy[j] := y_y[j] + (1/6)*(rk1[j]+2*rk2[j]+2*rk3[j]+rk4[j])*dx; 446 x[i] := yy[0]; 447 y[i] := yy[1]; 448 z[i] := yy[2]; 449 end; 450 end; 451 EndProgram; 452 Data; 453 //0 10 15 20 454 1 11.80 15.37 20.77 455 2 14.04 17.04 22.23 456 3 15.44 16.85 21.16 457 4 17.80 18.07 22.49 458 5 18.60 19.43 24.46 459 6 19.22 20.12 23.58 460 7 21.77 21.83 24.51 461 8 22.17 22.11 25.38 462 9 23.41 23.37 25.53 463 10 23.17 24.92 26.69 464 11 24.56 25.55 29.21 465 12 25.85 26.06 28.00 466 13 24.64 28.94 30.32 467 14 25.15 28.94 30.41 468 15 26.92 30.06 31.87 469 16 26.37 29.29 31.87 470 17 26.71 31.48 34.60 471 18 26.61 31.86 33.57 472 19 27.13 33.84 36.75 473 20 29.32 32.95 36.36 474 21 28.24 33.03 36.23 475 22 28.42 32.50 36.01 476 23 28.11 33.12 39.19 477 24 28.98 35.32 37.29 478 25 30.23 35.56 37.79 479 26 30.21 34.86 42.05 480 27 29.11 35.40 42.67 481 28 30.42 36.20 40.74 482 29 28.84 35.91 40.53 483 30 29.44 36.50 43.33
使用1.5的小例子:
比如我知道一个二次函数的一系列离散点,相求这个二次函数的系数:
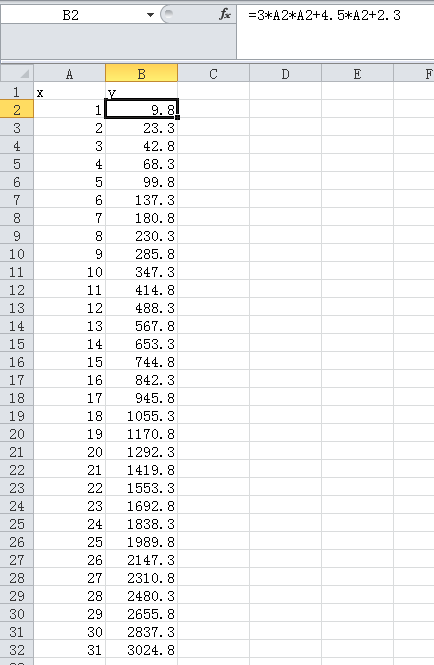
Title "Type your title here"; //Parameters ; //Variable ; //Function ; Variable x,y; Parameters a,b,c; Function y=a*x*x+b*x+c; Data; 1 9.8 2 23.3 3 42.8 4 68.3 5 99.8 6 137.3 7 180.8 8 230.3 9 285.8 10 347.3 11 414.8 12 488.3 13 567.8 14 653.3 15 744.8 16 842.3 17 945.8 18 1055.3 19 1170.8 20 1292.3 21 1419.8 22 1553.3 23 1692.8 24 1838.3 25 1989.8 26 2147.3 27 2310.8 28 2480.3 29 2655.8 30 2837.3 31 3024.8
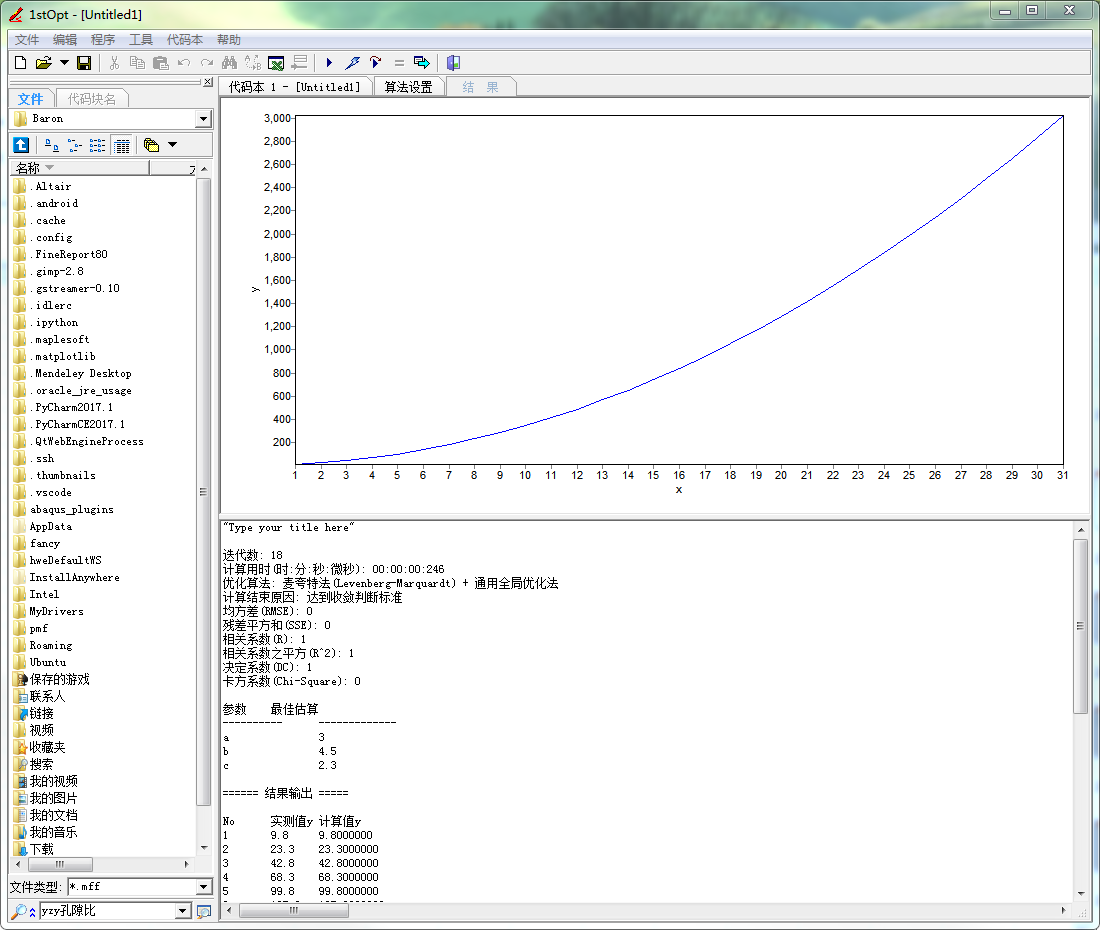
是不是挺完美的,哈哈
实战:

1 Title "Type your title here"; 2 //Parameters ; 3 //Variable ; 4 //Function ; 5 Parameters a,b,c; 6 Variable x,y; 7 Function y=-(a+b*c)*LN(c-x)-b*x+(a+b*c)*LN(c); 8 Data; 9 //x y 10 38.3612 38.09276591 11 71.3481 96.65369746 12 101.926 154.780949 13 133.801 156.4442223 14 164.935 334.699552 15 195.698 594.6346182 16 232.391 1529.185089
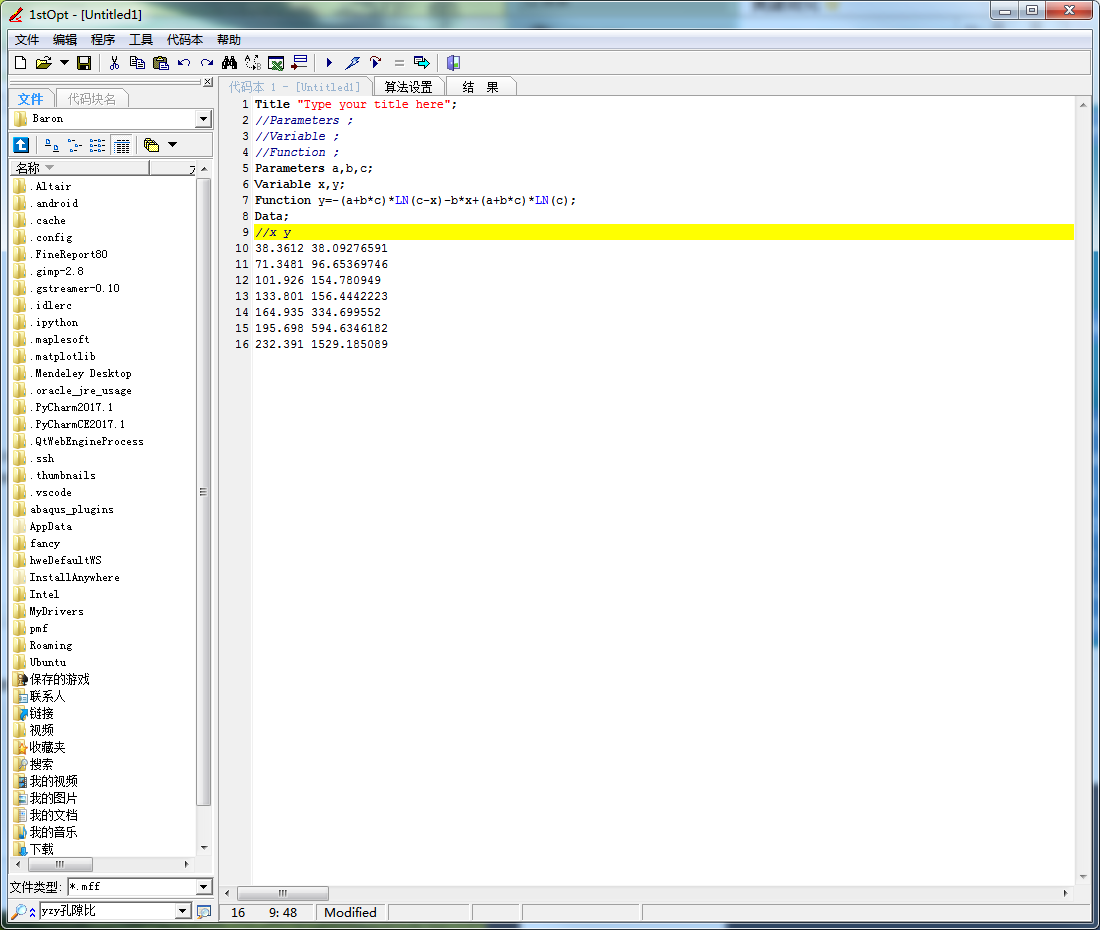
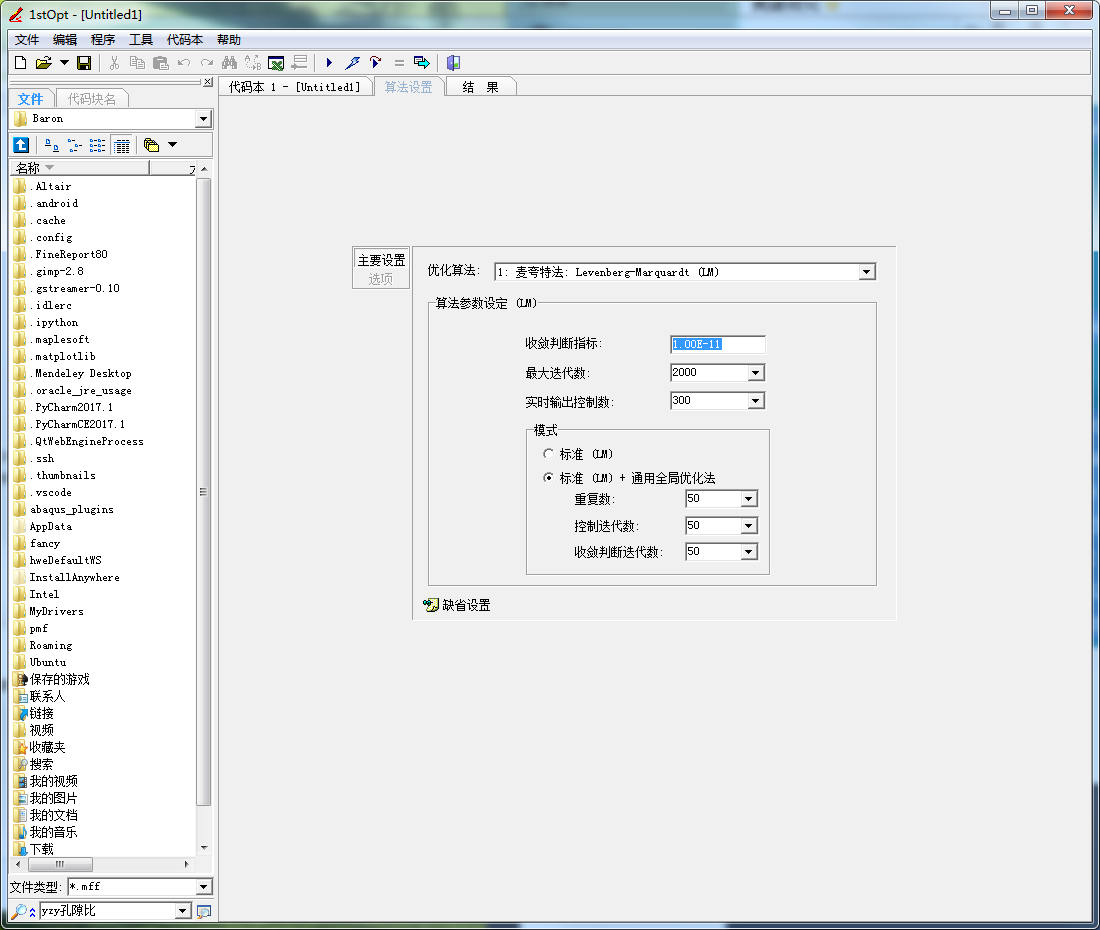

蓝线是离散点,红线是计算点





