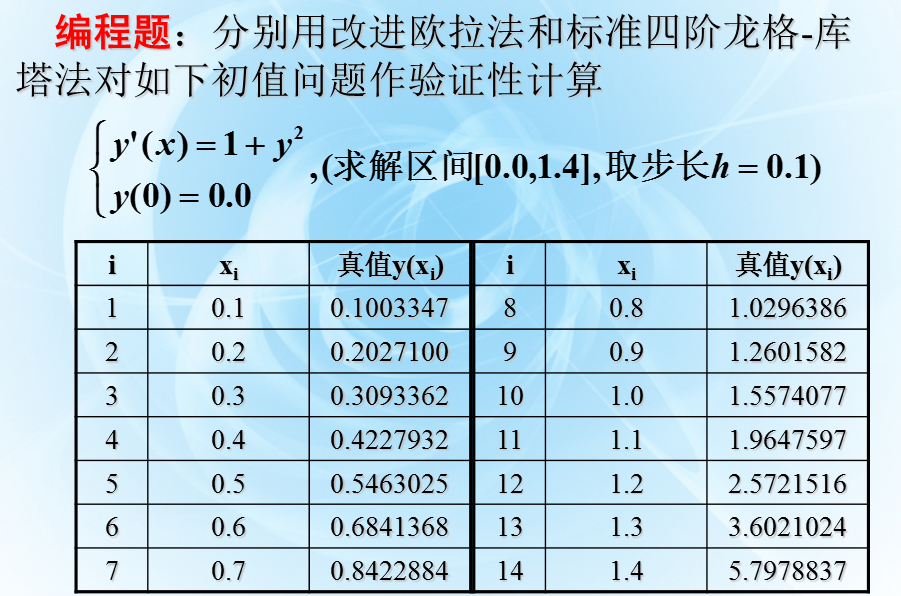
c语言-四阶龙格-库塔法

1 #include<stdio.h> 2 #include<math.h> 3 #define n 14 4 //double func1(double x, double y); 5 double func2(double x, double y); 6 int main(){ 7 double a = 0.0, b = 1.4;//求解区间为[a,b] 8 double h, m = 0.0;//h为步长,取0.1; m为y的初值。 9 double x[n + 1] = { 0.0 }, y[n + 1] = { 0.0 };//初始化数组 10 h = (b - a) / n;//求步长 11 x[0] = a; 12 y[0] = m; 13 printf("要求解的常微分方程为:dy/dx=1+y^2,初值为y(0)=0.0;\n"); 14 printf("下面为预估校正法结果:\n"); 15 //下面为预估校正法(即向前欧拉法和梯形法的结合,也称改进的欧拉法) 16 for (int i = 1; i <= n; i++) 17 { 18 y[i] = y[i - 1] + h*(1 + y[i - 1] * y[i - 1]); 19 x[i] = a + i*h; 20 y[i] = y[i - 1] + h*0.5*((1 + y[i - 1] * y[i - 1]) + (1 + y[i] * y[i])); 21 printf("x[%d]=%e , y[%d]=%e\n", i, x[i], i, y[i]); 22 } 23 printf("下面为四阶龙格-库塔法结果:\n"); 24 double k1 = 0.0, k2 = 0.0, k3 = 0.0, k4 = 0.0; 25 for (int i = 1; i <= n; i++) 26 { 27 x[i] = 0.0, y[i] = 0.0; 28 } 29 x[0] = a; 30 y[0] = m; 31 for (int i = 1; i <= n; i++) 32 { 33 k1 = h*func2(x[i - 1], y[i - 1]); 34 k2 = h*func2(x[i - 1] + h / 2.0, y[i - 1] + 0.5*k1); 35 k3 = h*func2(x[i - 1] + h / 2.0, y[i - 1] + 0.5*k2); 36 k4 = h*func2(x[i - 1] + h, y[i - 1] + k3); 37 y[i] = y[i - 1] + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4); 38 printf("x[%d]=%e , y[%d]=%e\n", i, x[i], i, y[i]); 39 x[i] = a + i*h; 40 } 41 return 0; 42 } 43 /* 44 double func1(double x, double y)//dy/dx=x-y+1,func1=x-y+1; 45 { 46 double f = 0; 47 f = x - y + 1; 48 return f; 49 } 50 */ 51 double func2(double x, double y)//dy/dx=1+y*y,func2=1+y*y; 52 { 53 double f = 0.0; 54 f = 1 + y*y; 55 return f; 56 }


-*--------------------------
R-K法一般形式:





