MATLAB 实现sobol、morris参数敏感性分析

 

% sobol 参数敏感性分析
%参考：
% csdn : https://blog.csdn.net/xiaosebi1111/article/details/46517409
% wiki： https://en.wikipedia.org/wiki/Variance-based_sensitivity_analysis
%运行环境 matlab2016b
%作者 blzhu@buaa.edu.cn 2020年6月7日
%% 初始化
clc;
clear all;
close all;
%% 设定：给定参数个数和各个参数的范围
D=3;% 维度3,几个参数
M=D*2;% 
nPop=4;% 采样点个数,也就是参数水平数 ,取大了好，比如4000，但慢
VarMin=[0 0 0 ];%各个参数下限
VarMax=[1 1 1];%各个参数上限
%% 产生所需的各水平参数
VarMin=[VarMin,VarMin];
VarMax=[VarMax,VarMax];
p= sobolset(M);% https://www.cnblogs.com/zhubinglong/p/12260292.html
% R=p(1:nPop,:);% 我只用前nPop个
R=[];
for i=1:nPop
    r=p(i,:);
    r=VarMin+r.*(VarMax-VarMin);
    R=[R; r];
end
% plot(R(:,1),'b*')
% 拆分为A B
A=R(:,1:D);% 每行代表一组参数，其中每列代表每组参数的一个参数；行数就代表共有几组参数
B=R(:,D+1:end);
% 根据A B 产生矩阵AB
AB=zeros(nPop,D,D);
for i=1:D
    tempA=A;
    tempA(:,i)=B(:,i);
    AB(1:nPop,1:D,i)=tempA;
end
%% 求各参数解
YA=zeros(nPop,1);% 解
YB=zeros(nPop,1);
YAB=zeros(nPop,D);%分别代表YAB1,YAB2,YAB3，YAB(:,D)就代表YABD
for i=1:nPop
    YA(i)=myfun(A(i,:));
    YB(i)=myfun(B(i,:));
    for j=1:D
        YAB(i,j)=myfun(AB(i,:,j));
    end
end
%%  根据一阶影响指数公式：
VarX=zeros(D,1);% S的分子
S=zeros(D,1);

% 0: 估算基于给定样本的方差(EXCEL var.p) ;   1:计算基于给定的样本总体的方差(EXCEL var.p())
% var([2.091363878    1.110366059    3.507651769    1.310950363    2.091363878    3.507651769    1.110366059    1.7066512],1);
VarY=var([YA;YB],1);% S的分母。 计算基于给定的样本总体的方差(EXCEL var.p())
for i=1:D
    for j=1:nPop
         VarX(i)=VarX(i)+YB(j)*(YAB(j,i)-YA(j));
    end
     VarX(i)=1/nPop*VarX(i);
     S(i)=VarX(i)/VarY;
end

%% 总效应指数
EX=zeros(D,1);
ST=zeros(D,1);
for i=1:D
    for j=1:nPop
         EX(i)=EX(i)+(YA(j)-YAB(j,i))^2;
    end
      EX(i)=1/(2*nPop)* EX(i);
     ST(i)=EX(i)/VarY;
end
disp('一阶影响指数：S');
disp(S);
disp('总效应指数：ST');
disp(ST);
disp('success!');


%% 子函数 matlab2016之前不支持子函数写在同一个m文档中
function y=myfun(x)
y=sin(x(1))+7*(sin(x(2)))^2+0.1*x(3)^4*sin(x(1));
end

 

Morris敏感性分析：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%  作者：朱丙龙；联系邮箱：zhubinglong@rails.cn；编程语言：matlab  2022b
%
%  日期：2024年4月25日16:38:49
%
%  功能：Morris分析例子
%
%  参考文献：
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc; % 清除命令窗口
clear all; % 清除工作空间的所有变量
close all; % 关闭所有打开的图形窗口

% 定义参数范围：三个参数，每个参数的取值范围分别是 [0, 10]、[-pi, pi] 和 [0, 1]
param_ranges = [0, 10; -pi, pi; 0, 1];

% 设定参数的离散化水平数
num_levels = 10;

% 设定重复实验的次数，用于增加结果的稳定性
num_r = 30;

% 调用 morris_method 函数执行 Morris 方法敏感性分析
[mu, sigma] = morris_method(@model_example, param_ranges, num_levels, num_r);
disp(['各参数的平均敏感度:' num2str(mu')]);% 输出各参数平均敏感度

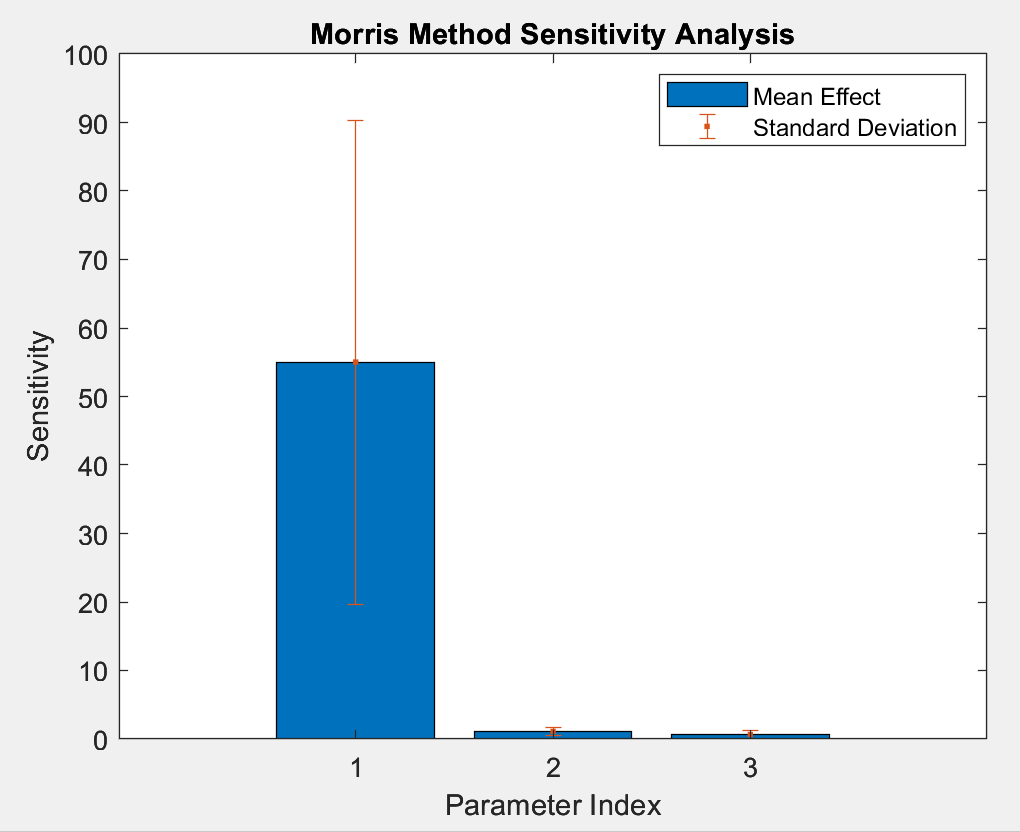
% 创建一个柱状图来显示每个参数的平均影响（mu）
figure;
bar(1:length(mu), mu);
hold on;

% 在柱状图上添加误差条，显示每个参数的标准偏差（sigma）
errorbar(1:length(mu), mu, sigma, '.');

% 设置图表的标签和标题
xlabel('Parameter Index'); % x轴标签：参数索引
ylabel('Sensitivity'); % y轴标签：敏感性
title('Morris Method Sensitivity Analysis'); % 图表标题：Morris 方法的敏感性分析
legend('Mean Effect', 'Standard Deviation'); % 图例：表示平均效应和标准偏差

% 子程序：模型示例函数
function y = model_example(x)
    % MODEL_EXAMPLE 示例模型函数
    % 输入参数:
    % x - 向量，包含三个元素 [x1, x2, x3]
    % 输出参数:
    % y - 根据模型函数计算得到的输出结果
    % 模型计算公式为 x1 的平方加上 x2 的正弦值加上 x3 的立方
    y = x(1)^2 + sin(x(2)) + x(3)^3;
end

% 主函数：执行 Morris 方法的函数
function [mu, sigma] = morris_method(model_func, param_ranges, num_levels, num_r)
    % morris_method 执行 Morris 方法的全局敏感性分析
    % 输入参数:
    % model_func - 模型函数句柄
    % param_ranges - 参数的范围，每行对应一个参数的最小值和最大值
    % num_levels - 参数的离散化水平数
    % num_r - 重复实验的次数
    % 输出参数:
    % mu - 参数的平均影响大小，向量形式
    % sigma - 参数影响的标准偏差，向量形式

    % 获取参数数量
    num_params = size(param_ranges, 1);
    % 计算 delta，公式来自 Morris 方法的定义
    delta = num_levels / (2 * (num_levels - 1));
    % 创建单位矩阵，用于生成扰动向量
    ee = eye(num_params);
    % 初始化输出向量
    mu = zeros(num_params, 1);
    sigma = zeros(num_params, 1);
    
    % 主循环，按指定次数重复实验
    for r = 1:num_r
        % 随机生成基线输入参数
        base = param_ranges(:, 1) + (param_ranges(:, 2) - param_ranges(:, 1)) .* ...
               lhsdesign(num_params, 1, 'smooth', 'off') * (num_levels - 1) / num_levels;
        % 随机确定参数变化的方向
        direction = randi([0 1], num_params, 1) * 2 - 1;
        % 计算基线模型输出
        output_base = model_func(base);
        
        % 对每个参数进行扰动
        for i = 1:num_params            
            perturbed = base + direction .* ee(:, i) .* delta .* (param_ranges(:, 2) - param_ranges(:, 1));
            output_perturbed = model_func(perturbed);
            effect = abs(output_perturbed - output_base);
            mu(i) = mu(i) + effect;
            sigma(i) = sigma(i) + effect^2;
        end
    end
    
    % 计算每个参数的平均影响和标准偏差
    mu = mu / num_r;
    sigma = sqrt(sigma / num_r - mu.^2);
end