《算法竞赛入门经典》6.1.2栈和队列-铁轨

　　某城市有一个火车站，铁轨铺设如下图所示。有n节车厢从A方向驶入车站，按进站顺序编号为1~n。你的任务是让它们按照某种特定的顺序进入B方向的铁轨并使出车站。为了重组车厢，你可以借助中转站C；这是一个可以停放任意多节车厢的车站，但由于末端封顶，驶入C的车厢必须按照相反的顺序驶出C。对于每个车厢，一旦从A进入C，就不能再回到A了；一旦从C进入B，就不能回到C了。换言之，在任意时刻，只有两种选择：A->C和C->B。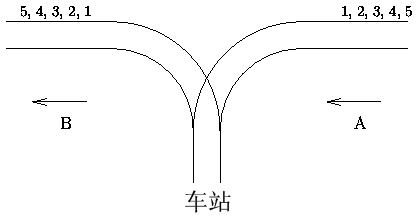
样例输入：
5
1 2 3 4 5
5
5 4 1 2 3
6
6 5 4 3 2 1
样例输出：
Yes
No
Yes

#include <stdio.h>
#define MAXN 1000 + 10
int n, target[MAXN];

int main(void)
{
    while(scanf("%d", &n) == 1)
    {
        int stack[MAXN], top = 0;
        int A = 1, B = 1;
        for(int i = 1; i <= n; i++)
            scanf("%d", &target[i]);
        int ok = 1;
        while(B <= n)
        {
            if(A == target[B]) { A++; B++; }    //车厢按顺序进出中转站C，则跳出循环
            else if(top && stack[top] == target[B]) { top--; B++; }//若车厢按逆序进中转站C，则跳出循环
            else if(A <= n) stack[++top] = A++;    //调整车厢为逆序出中转站C
            else { ok = 0; break; }                //车厢既不是按顺序，也不是按逆序进出中转站C
        }
        printf("%s\n", ok ? "Yes" : "No");
    }
    return 0;
}

分析：
　　1.栈：在中转站C中，车厢符合后进先出的原则，称为栈，即LIFO表；其中LIFO代表Last In First Out。由于栈只有一端生长，实现时只需要一个数组stack和栈顶指针（始终指向栈顶元素）。
　　2.对于第二种输入情况：
　　　　B <= n        A <= n       stack[++top] = A++;
　　　　1 <= 5        1 <= 5        stack[1] = 1; top = 1; A = 2;
           　　　　 　　2 <= 5        stack[2] = 2; top = 2; A = 3;
            　　　　　　3 <= 5        stack[3] = 3; top = 3; A = 4;
            　　　　　　4 <= 5        stack[4] = 4; top = 4; A = 5;
            　　　　　　5 <= 5        stack[5] = 5; top = 5; A = 6;
　　　　top&&stack[top]==target[B]               top--; B++;
　　　　5 && 5==5                               　　　top = 4 ; B = 2;
　　　　4 && 4==4                              　　　 top = 3 ; B = 3;
　　　　3 && 3==1                              　　　 跳出while循环
　　3.为了方便，数组下标均从1开始。例如：target[1]是指目标序列中第一个车厢的编号，stack[1]是指栈底元素（栈空当且仅当top=0）。

C++提供了一种更加简单的处理方式—STL队列：

#include <cstdio>
#include <stack>
using namespace std;
#define MAXN 1000 + 10
int n, target[MAXN];

int main(void)
{
    while(scanf("%d", &n) == 1)
    {
        stack<int> s;
        int A = 1, B = 1;
        for(int i = 1; i <= n; i++)
            scanf("%d", &target[i]);
        int ok = 1;
        while(B <= n)
        {
            if(A == target[B]) { A++; B++; }    //车厢按顺序进出中转站C，则跳出循环
            else if(!s.empty() && s.top() == target[B]) { s.pop(); B++; }//若车厢按逆序进中转站C，则跳出循环
            else if(A <= n) s.push(A++);        //调整车厢为逆序出中转站C
            else { ok = 0; break; }                //车厢既不是按顺序，也不是按逆序进出中转站C
        }
        printf("%s\n", ok ? "Yes" : "No");
    }
    return 0;
}