DLX之数独问题的解决

      数独是一个非常经典的智力游戏。它的游戏的规则是这样的：在一个9x9的方格中，你需要把数字1-9填写到空格当中，并且使方格的每一行和每一列中都包含1-9这九个数字。同时还要保证，空格中用粗线划分成9个3x3的方格也同时包含1-9这九个数字。
如下例题：

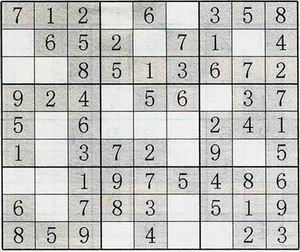
其解为：

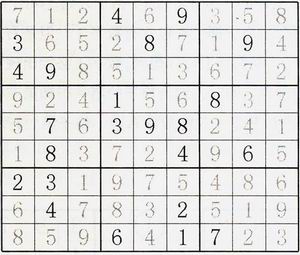
      在计算科学理论中，这一类问题的解答被称之为NPC问题中的Hitting Set Problem，中文名应该叫做碰集问题。该类问题可以通过转换成为精确覆盖问题，其中以行表示概然，以列表示常规约束。
      在数独问题中，行所表示的概然状态很明显为（r,c,k）即行，列，放置的数字。而列所表示的约束大致整理了下，分做四种，即r行中放置数k可行性，c列放置数k可行性，放置于(r,c)格子可行性以及块b(即所属区域)放置数k的可行性。因此行总共有N*N*N=9*9*9=729个，列总共有9*9*4=324个，问题转化为在729*324的矩阵中取若干行，使每个列只有一个'1'，此时对应一个数独的解，而(r,c)格的约束保证了我们最后解的行数一定<=N*N。至此，模型转化完成。

      以下是我实现的代码，可以适合N*N的任意大小数独问题，其中nil表示未填写部分的ascii，flag表示最小数字ascii，所有输入必须转化到grid[i][j]中。

#include <iostream>
using namespace std;


const int N=9;//规模大小
const int Per=3;//sqrt(N);
char grid[N+2][N+2];//存储格
char res[N+2][N+2];//答案
const int MAXR=N*N*N;
const int MAXC=N*N*4;
const int MAXLEN=4*N*MAXC+MAXC+MAXR;
const int st[4]={0,N*N,2*N*N,3*N*N};
int L[MAXLEN];
int R[MAXLEN];
int D[MAXLEN];
int U[MAXLEN];
int nRow[MAXLEN];
int nCol[MAXLEN];

int Col[MAXC]; //判定列集是否已插入
int Row[MAXR]; //判定行集是否已插入
//int RC[MAXR][MAXC]; //判定元素是否已插入
int RS[MAXR],CS[MAXC]; //行长与列长
int eid; //内存标识
int head;
int Cn;
int ans[MAXR];
int alen;

char flag;
char nil;
//DLX算法 进行精确覆盖 判定前请先判断是否各列中都有1存在
//对于行列唯一的情况 可以考虑将RC数组取消以加速
inline void init()
{
    memset(Row,-1,sizeof(Row));
    memset(Col,-1,sizeof(Col));
//    memset(RC,-1,sizeof(RC));
    memset(nCol,-1,sizeof(nCol));
    memset(nRow,-1,sizeof(nRow));

    head=0;
    L[head]=R[head]=D[head]=U[head]=head;
    eid=1;
    Cn=0;
}

//插入行

inline void insRow(int r)
{
    
    U[D[head]]=eid;
    U[eid]=head;
    D[eid]=D[head];
    D[head]=eid;
    
    L[eid]=R[eid]=eid;
    
    RS[r]=1;
    Row[r]=eid++;
}

//插入列

inline void insColumn(int c)
{
    L[R[head]]=eid;
    L[eid]=head;
    R[eid]=R[head];
    R[head]=eid;
    
    U[eid]=D[eid]=eid;
    
    CS[c]=1;
    Col[c]=eid++;
}

//插入元素

inline void insElement(int r,int c)
{
    int rid=Row[r];
    int cid=Col[c];
    
    L[R[rid]]=eid;
    L[eid]=rid;
    R[eid]=R[rid];
    R[rid]=eid;
    
    
    U[D[cid]]=eid;
    U[eid]=cid;
    D[eid]=D[cid];
    D[cid]=eid;
    
    
    nRow[eid]=r;
    nCol[eid]=c;
    
    ++CS[c];
    ++RS[r];

//    RC[r][c]=eid;
    ++eid;
}

//插入操作

inline void insert(int r, int c)
{

    if (Col[c]==-1)
    {
        ++Cn;
        insColumn(c);
    }

    if(Row[r]==-1)
    {
        insRow(r);
    }

//    if(RC[r][c]==-1)
    {
        insElement(r,c);
    }

}

//删除列(使用cid)

inline void RemoveCol(int c)
{
    //c=Col[c];

    L[R[c]]=L[c];
    R[L[c]]=R[c];

    int i,j;

    for (i=D[c];i!=c;i=D[i])
    {
        for (j=R[i];j!=i;j=R[j])
        {
            if(nCol[j]==-1) continue;
            U[D[j]]=U[j];
            D[U[j]]=D[j];
            --CS[nCol[j]];
        }
    }

}

//恢复列(使用cid)
inline void ResumeCol(int c)
{
    //c=Col[c];

    int i,j;

    for (i=U[c];i!=c;i=U[i]) 
    {
        for (j=L[i];j!=i;j=L[j]) 
        {
            if(nCol[j]==-1) continue;
            ++CS[nCol[j]];
            U[D[j]]=j;
            D[U[j]]=j;
        }
    }

    L[R[c]]=c;
    R[L[c]]=c;
}

//精确覆盖

inline bool dfs(int k)
{

    if (R[head]==head)
    {
        alen=k;
        return true;
    }

    int i,j;

    int s=INT_MAX;
    int c;

    for (i=R[head];i!=head;i=R[i])
    {
         if(nCol[D[i]]==-1) {c=i;continue;}
        if (CS[nCol[D[i]]]<s)
        {
            s=CS[nCol[D[i]]];
            c=i;
        }
    }

    RemoveCol(c);

    for (i=U[c];i!=c;i=U[i])
    {
        ans[k]=nRow[i];
        for (j=L[i];j!=i;j=L[j])
        {
            if (nCol[j]==-1)
            {
                continue;
            }
            RemoveCol(Col[nCol[j]]);
        }
        
        if(dfs(k+1))
        {
            return true;
        }

        for (j=R[i];j!=i;j=R[j])
        {
            if (nCol[j]==-1)
            {
                continue;
            }
            ResumeCol(Col[nCol[j]]);
        }
    }

    ResumeCol(c);    
    return false;
}


inline int BoxNum(int i,int j)
{
    return (i/Per)*Per+j/Per;
}

inline void Sudoku()
{

    init();
    int i,j,k;
    int R,C;
    
    for (i=0;i<N;++i)
    {
        for (j=0;j<N;++j)
        {
            int ind=N*i+j;
            int BN=BoxNum(i,j);
            
            if (grid[i][j]==nil)
            {
                for (k=0;k<N;++k)
                {
                    R=N*N*k+N*i+j;
                    
                    C=st[0]+ind;
                    insert(R,C);
                    
                    
                    C=st[1]+N*i+k;
                    insert(R,C);
                    
                    
                    C=st[2]+N*j+k;
                    insert(R,C);
                    
                    C=st[3]+N*BN+k;
                    insert(R,C);                                
                }
            }
            else
            {
                R=N*N*(grid[i][j]-flag)+N*i+j;
                C=st[0]+ind;
                insert(R,C);
                
                C=st[1]+N*i+(grid[i][j]-flag);
                insert(R,C);
                
                C=st[2]+N*j+(grid[i][j]-flag);
                insert(R,C);
                
                C=st[3]+N*BN+(grid[i][j]-flag);
                insert(R,C);
            }
        }
    }
    
    if (Cn==MAXC&&dfs(0))
    {
        int r,c,k;
        for(i=0;i<alen;++i)
        {        
            c=ans[i]%N;
            ans[i]/=N;
            
            r=ans[i]%N;
            ans[i]/=N;
            
            k=ans[i];
            
            res[r][c]=k+flag;
        }        
        for (i=0;i<N;++i)
        {
            for (j=0;j<N;++j)
            {
                putchar(res[i][j]);
            }
            puts("");
        }
    }
    else
    {
        puts("Could not complete this grid.");
    }

}