时间复杂性O(f(n))

概述

T(n) =次数表示式，表示的是执行的次数； O(n) 通过T(n)的抓大头等操作后这就是时间复杂度，有O(1)、O(logn)、O(n)、O( nlogn)、O(n^2)、O(n^3)、O(2^n) 这些

 

 

O(1)

没有for循环体的最上而下的时间复杂性是O(n)

 

O(n)

有一层for循环的

 比如：for(i=1; i=n; i+=2); 的时间复杂度为 A. O(n)    # 这种i+=2,i-=2这种是O(1/2 n)，但还是O(n)， 如果是i*=2就不一样了。

递归也是O(n) : 

 

 

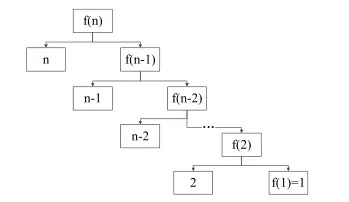
O(n^k) 

有k层for 循环的

特别地：for (int i=0; i < n; ++i) {

for (int j=i; j < n; ++j) {...}

}

这种只需算最深层执行的次数即可，T(n) = n + (n-1) + (n-2) + (n-3) + ... +2+1 = Sn = [(1+n)n]/2 即时间复杂度为O(n^2), 也是符合a层循环，时间复杂度为O(n^a) 的。

O( loga(n) )

上一次查找的量是本次的a倍 

如果说一个算法的时间复杂度是log2n，那么这个程序有可以是二分查找算法。因为它对n个进行2分查找最多是log2n次。再比如：

int i = 1;
while(i<n)
{
    i = i * 2;
}

从上面代码可以看到，在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。我们试着求解一下，假设循环x次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 x 次方等于 n，那么 x = log2^n

 

线性对数阶O(nlogN)

其实非常容易理解，将时间复杂度为O(logn)的代码循环N遍的话，那么它的时间复杂度就是 n * O(logN)，也就是了O(nlogN)。

for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

 

 

 

注意点

一、注意，1、如果有两个同级的for循环取最大的。 O(n) < O(n^2)

二、有if else语句的，取大的

三、还有一个空间复杂度