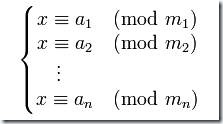剩余定理，同余方程，欧几里德算法

1.“孙子问题”

“孙子问题”在现代数论中是一个一次同余问题，它最早出现在我国公元四世纪的数学著作《孙子算经》中。《孙子算经》卷下“物不知数”题说：有物不知其数，三个一数余二，五个一数余三，七个一数又余二，问该物总数几何？显然，这相当于求不定方程组：
N=3x+2,N=5y+3,N=7z+2

《孙子算经》所给答案是N=23。由于孙子问题数据比较简单，这个答数通过试算也可以得到。中国数学家秦九韶于1247年做出了完整的解答，口诀如下：
三人同行七十希，五树梅花廿一支，七子团圆正半月，除百零五使得知。

这个解法实际上是，首先利用秦九韶发明的大衍求一术求出5和7的最小公倍数35的倍数中除以3余数为1的最小一个70（这个称为35相对于3的数论倒数），3和7的最小公倍数21相对于5的数论倒数21，3和5的最小公倍数15相对于7的数论倒数15。然后70×2+21×3+15×2－2×105=233便是可能的解之一。它加减3、5、7的最小公倍数105的若干倍仍然是解，因此最小的解为233除以105的余数23。

附注：这个解法并非最简，因为实际上35就符合除3余2的特性，所以最小解是：35×1+21×3+15×2－105=23。最小解加上105的正整数倍都是解。

2.分析

下面分析一下孙子算经的算法，一个数满足除以3余2，除以5余3，除以7余2.那么我们先假设这个数N = A+B+C。如果A除以3余2（A≡2（mod3））且B和C是3的倍数。B除以5余3（B≡3（mod5））且A,C都是5的倍数，C除以7余2（C≡2（mod7））且A，B都是7的倍数。那么N就是我们要找的数。总结下来，A应该满A≡2（mod3）且A是5和7的公倍数；B≡3（mod5）,且B是3和7的公倍数；C≡2（mod7）,且C是3和5的公倍数。我们设A=k1*35（35是5和7的最小公倍数，则k1*35可以表示5和7的所有公倍数，k1是正整数）b=k2*21,C=k3*15;再取合适的k1,k2,k3的值使得A≡2（mod3），B≡3（mod5）,C≡2（mod7）.可得A=140，B=63，C=30.则N=233，又因为3，5，7的最小公倍数是105，在减去105得23.故所得最小整数为23，N=23+K*105都满足条件。

我们可以将上诉问题改为求一次同余方程的形式即：K1*35≡1（mod3）求出K1*35的最小值为70，k1=2;K2*21≡1（mod5）求出K2*21的最小值为21，k2=1;K3*15≡1（mod7）求出K3*15的最小值为15，k3=1;我们想得到A模3余1题中要求余2，所以用70再乘以2就得到A这时A模3就余2了，同理用21*3，15乘以2。再相加得到N=2*35*2+1*21*3+1*15*2=233。233所在的模105的剩余类都满足条件即N=23+K*105.

3.中国剩余定理

以上解法若推广到一般情况，便得到了中国剩余定理的一个构造性证明。

一般地，中国剩余定理是指若有一些两两互质的整数 ，则对任意的整数：a1,a2,...an，以下联立同余方程组对模有公解：

4.乘法逆元

例如：4关于模7的乘法逆元为多少？

4*X≡1(mod 7)

这个方程等价于求一个X和K，满足

4X=7K+1

其中X和K都是整数。

若ax=1 mod f 则称a关于模f的乘法逆元为x。也可表示为ax≡1(mod f)。

当a与f互素时，a关于模f的乘法逆元有唯一解。如果不互素，则无解。如果f为素数，则从1到f-1的任意数都与f互素，即在1到f-1之间都恰好有一个关于模f的乘法逆元。

例如，求5关于模14的乘法逆元：

14=5*2+4

5=4+1

说明5与14互素，存在5关于14的乘法逆元。

1=5-4=5-(14-5*2)=5*3-14

因此，5关于模14的乘法逆元为3。

在模运算中，

加法单位元是0，因为(0+a) mod m = a mod m；

乘法单位元是1，因为(1×a) mod m = a mod m

定义 对a∈Zm，存在b∈Zm，使得a+b ≡ 0 (mod m)，则b是a的加法逆元，记b= - a。

定义 对a∈Zm，存在b∈Zm，使得a×b ≡1 (mod m)，则称b为a的乘法逆元。

5.求同余方程

其求法可用欧几里德算法：

Extended Euclid (d，f) //算法求d关于模f的乘法逆元d-1 ，即 d* d-1 mod f = 1

1 。(X1，X2，X3) := (1，0，f)； (Y1，Y2，Y3) := (0，1，d)

2。 if (Y3=0) then return d-1 = null //无逆元

3。 if (Y3=1) then return d-1 = Y2 //Y2为逆元

4。 Q := X3 div Y3 //整除

5。 (T1，T2，T3) := (X1 - Q*Y1，X2 - Q*Y2，X3 - Q*Y3)

6 。(X1，X2，X3) := (Y1，Y2，Y3)

7。 (Y1，Y2，Y3) := (T1，T2，T3)

8。 goto 2

常用于加密算法中。