静态时序分析（STA）基础

注：上海交大论文《数字电路静态时序分析与设计》—学习笔记

第一章 概述

1.4 集成电路的设计流程

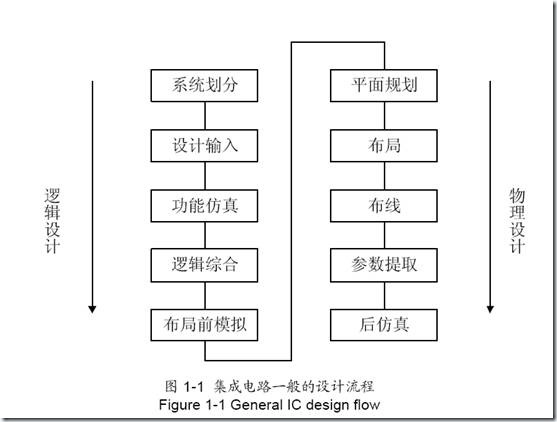
一般集成电路设计步骤分为逻辑设计和物理设计如图1-1 所示：

逻辑设计包括：

系统划分：将一个大规模的系统按功能分成几个功能模块

设计输入：用HDL(Hardware Description Language)语言或电路原理图的形式对系统进行功能级描述的设计输入。

功能仿真：对功能级描述进行功能和时序仿真验证并在验证功能正确后转变成适用于综合器的RTL级(Register Transfer Level)描述的网表输入。

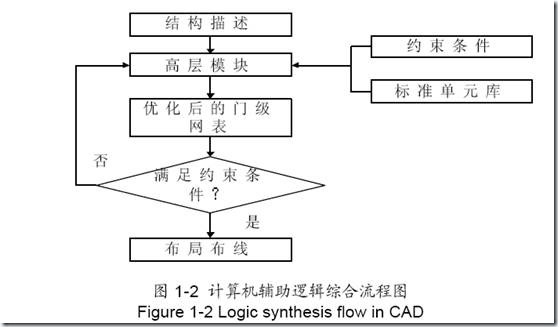
逻辑综合：把高层次设计的描述利用某种标准单元库按照一定的约束条件转换成优化的门级网表。图1-2给出了基本的计算机辅助逻辑综合的流程图。设计者只要把精力集中在层次的划分、高层的设计、描述准确的约束条件和标准单元库的单元优化上，而其它大量的工作由逻辑综合工具自动完成逻辑综合工具经过多次交互处理最终产生最优化的门级网表。

布局前的模拟：对综合后加入单元时延信息的门级网表进行仿真检查时序上是否满足设计系统规范和接口规范。

物理设计包括：

平面规划：其任务是为每个模块和整个芯片选择一个好的布图方案一般根据其包含器件数估计模块的面积再根据该模块和其它模块的连接关系和上层模块或芯片的形状估计该模块的形状和相对位置此过程一般手工完成

布局：确定模块中各单元的位置布局问题比较复杂一般分成初线始布局和改进布局两步。

布线：通常布线分为总体布线(Global Routing)和详细布线(Detailed Routing)两步总体布线把线网分配到合适的布线区域不关心走线的具体位置详细布线最终确定连线的具体位置。

参数提取：确定各个连接处的电阻和电容及互连线的分布参数。

后仿真：加入布局布线所增加的各种寄生电学参数后再次进行时序仿真并进行ERC，电学规则检查和DRC，设计规则检查最后进行网表的验证(LVS Layout Versus Schematic) 来确认版图的正确性。

1.5 数字集成电路的时序分析简介

数字集成电路的设计必须满足一定的时序关系最早是用SPICE 进行时序分析和时序验证,但是,SPICE 方法与原始输入模式有关, 因而在实际应用中受到一定的制在80 年代初期出现了与原始输入模式无关的拓扑算法,该算法简单高效,因而许多时序分析和验证工具中得到应用大约在80 年代后期,人们开始对拓扑算法中的伪路径问题进行广泛的研究提出了各种敏化路径的定义,并将其用于时序分析和时序验证中。

1.5.1 同步时序电路中的时序关系

在一个同步时序电路中, 所有的触发器都由一个共同的外部时钟线控制, 这条时钟线通常称为全局时钟(global clock)。为了实现严格的同步, 电路中的时序关系必须满足一定的条件。

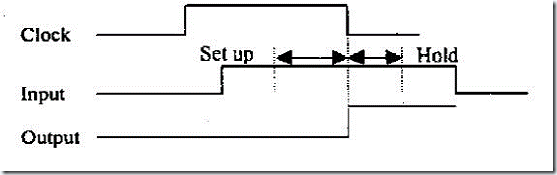
一个下降沿触发的触发器，它有3个端口，即数据输入端(data input)、数据输出端(data output)和控制端(control input)。它的基本工作原理是：当控制端口由高电平变化为低电平时触发器对数据输入端进行采样，并把采样值送到数据输出端。当控制端口为其它情况时数据输出端维持原采样值直至控制端口第二次由高电平变化为低电平它的时序关系如图1-3 所示：

图1-3 建立时间和保持时间

实际上由于物理元器件本身的特性,为了保证采样过程的准确，数据输入端必须在实际采样时间到达之前就保持稳定，同样在采样时间之后数据输入端仍然必须维持一段时间。这其实就是通常所说的数据输入端相对于采样时刻的数据建立时间(setup time) 和数据保持时间(hold time) 。如上图所示当触发器类型确定以后建立时间和保持时间由该触发器本身的结构决定,一般来说它们是常数。

1.5.2 时序驱动的逻辑综合

在一个典型的同步时序电路中，触发器的数据输入端连接到一个组合逻辑电路的输出，而该组合逻辑电路的输入又连接到一些触发器的数据输出端，如图1-4 所示：

图1-4 同步时序电路

由前面的分析知道，为了实现正确的同步，触发器的数据输入端必须满足一定的时序关系，而触发器的数据输入端通常连接到一个组合逻辑电路的输出因此,该组合逻辑电路必须满足一定的时序关系。

设时钟周期为tc，触发器的第一个下降沿发生在t= 0，则第二个下降沿发生在t= tc。考虑图2 中的组合逻辑电路，在t= 0时，该组合逻辑电路的原始输入端得到了触发器的输出数据，由这些确定的原始输入可以得到该组合逻辑电路的原始输出，设原始输出最晚在t=dmax时稳定，由于原始输出连接到触发器的数据输入端，为了实现正确的同步，dmax 必须满足下式:

tc – dmax > ts 或 dmax > tc - ts (1-1)

式中，ts为该触发器的数据建立时间。同样，对数据保持时间，也可以得到类似的结论当组合逻辑电路的原始输入在t=0 获得了触发器的输出数据，令dmin 为该组合逻辑电路最早实现输出稳定的时间，为了实现正确的同步，dmin 必须满足下式:

dmin > th (1-2)

式中，th 为该触发器的数据保持时间以上关系可以清楚地由图1-3 和图1-4 得到因此，如果我们要综合图1-4 中的组合逻辑电路，它的输入包括该组合逻辑电路要实现的逻辑功能以及必须满足的时序关系，该时序关系通常以下列形式反映:

(1) 原始输入的到达时间(arrival time AT)；

(2) 原始输出的要求时间(require time RT)；

其中，原始输入的到达时间反映了该组合逻辑电路所处的时间环境，原始输出的要求时间则直接限制了该组合逻辑电路的速度而逻辑综合的结果，不但要求该组合逻辑电路的逻辑功能正确, 而且它的时序关系必须满足(1-1) 式和(1-2) 式。

1.5.3 时序分析

在综合出一个组合逻辑电路之后，需要验证它是否满足给定的时序关系，这通常又称为时序验证(timing verification) 组合逻辑电路的时序验证需要计算该组合逻辑电路的dmax 和dmin，它通常又称为时序分析(timing analysis) 需要指出的是，数字集成电路时序分析的精确值完全由它的模拟行为所决定，一般情况下不易得到该精确值，因此，在时序分析时必须坚持以下两条原则:

1) 时序分析的结果相对于真实值必须是保守的如果令d'max 和d'min 是时序分析所得到的结果,而dmax 和dmin 是真实值, 则必须满足,

d'max ≥ dmax (1-3)

和

d'min ≤dmin (1-4)

考虑(1-1) 式和(1-3)式, 如果存在d'max ≥ tc - ts 则必然有dmax ≤tc – ts，也就是说，如果d'max 是满足时序关系的, 则dmax 必然也是满足时序关系的。同理，对dmin 也可得到类似的结论。

如果d'max 相对于dmax 不是保守，d'max ≤ dmax ，则并不能由d'max≥c- s 得到dmax≥c- s ，即验证的结果是正确的，而实际的结果有可能是错误的, 因此,会出现所谓的“假的正确结果”(false positive result)。

2) 时序分析的结果必须尽可能接近于真实值

保守的计算虽然可以进行有效的时序验证, 但是当保守的结果远远大于实际的精确值时也可能出现相应的错误即验证的结果是错误的, 而实际的结果是正确的，因此, 会出现所谓的“假的错误结果”(false negative result)。

因此, 在进行时序分析时，一方面要保证所得到的结果是保守的，另一方面，要保证所得到的结果尽可能与真实值接近这样，时序验证的结果才是有效的，不会出现假的正确结果和假的错误结果最后需要指出的是，在实际的时序验证中，通常只对dmax 进行验证而不考虑dmin , 其原因在于，假如dmin 违反了时序关系，只需用一个延时器就可以实现正确的时序关系以下我们只对dmax 进行分析。

1.5.4 SPICE 分析法

前面提到dmax 实际上由电路的模拟行为所决定为了得到准确的dmax可以用三极管电阻和电容等来模拟电路的行为显然, SPICE 非常适于解这类问题它通过对一个电路建立它的连续微分方程组来计算得到准确的dmax。而实际应用SPICE 进行时序分析时存在以下几个困难:

1) 由于一组微分方程只能求解一个原始输入模式的响应为了得到准确的dmax 必须对所有2n 个原始输入模式进行计算这里n 为原始输入变量个数。

2) 当电路规模超过一定限制时微分方程数目显著增加,计算微分方程的解必然要耗去大量的时间。

由于存在以上困难所以在实际的时序分析中并不应用SPICE 而是应用更抽象的门级分析法由于门级分析不与电路的模拟行为直接相关,同时又含有模拟行为的信息因而在实际中得到了广泛的应用。

1.5.5 门级时序分析

门级时序分析问题可以归纳如下：

布尔网络G=(V,E)，表示一个多级组合逻辑电路。V = Vpi U Vpo U Vi
式中VP I表示原始输入，VPO表示原始输出, Vi 表示内部节点,通常也称作门，表示网络中节点之间的边集。

任意一个内部节点nV。它的延迟特性[0,d(n)]由电路的模拟行为事先计算得到。对于每个原始输入XiVpi，它的它的到达时间为arr(Xi)；则对于任意一个原始输出ZiVpo,计算它的最晚到达时间arrmax (Zi)；

需要指出的是,在门级时序分析中,为了方便,假设每个门的延迟对不同的扇入以及上升和下降波形都是相同的,而实际上,门的延迟是扇入和上升以及下降波形的函数。

1.5.6 拓扑算法

对于门级时序分析问题,一个最简单和最直接的算法就是拓扑算法在拓扑算法中, 假定每个门的输出只有在它的各扇入均稳定以后才稳定因此, 简单地从原始输入到原始输出的正向遍历便可以得到原始输出的最晚到达时间,计算公式为:

从拓扑上讲, 网络中从原始输入到原始输出的最长路径决定了原始输出的最晚到达时间(此时,原始输入的到达时间假设为0)该算法的复杂度为O(|V|+|E|) 其中|V|为网络中节点的数目，|E|为网络中边的数目由于拓扑算法简单高效,并且它的计算结果是保守的,因而在许多时序优化工具中都用到该算法。

1.6 静态时序分析中要解决的主要问题

为了对电路进行门级的静态时序分析，首先需要整个电路的单元线网及其相互关系的信息这些信息主要从网表文件和库文件中得到库文件和网表文件都是普通的文本文件格式在进行需要把库和网表中有用的信息抽取出来链接成可以进行分析的数据结构。

有了库和网表的数据结构后要进行时序分析还需要得到各个单元和线网的时延单元的时延可以通过其输入信号的上升下降时间及输出端口上的负载电容信息。从工艺库中的查表模型中以插值的方法得到。

线网是由半导体材料内部的金属层实现的，可以看作微带结构。要求得线网的时延，首先要把线网结构转变成可以用于分析的树形RC结构或RLC结构，然后通过特定的方法从这种结构中计算出信号在线网上的时延。

在计算线网时延的同时还不能忽略一个问题就是串扰的问题。所谓串扰问题就是多根长的平行互连线之间信号的互相影响解决串扰问题。有两个方面，一个是求得两根平行线之间的耦合电容或耦合电感；另一个是根据不同的情况估算串扰对时延的影响。

当已经掌握了所有单元和线网的时延情况后，还必须在所有的从触发器与触发器间的组合逻辑块中找到最长路径和最短路径，以便进行建立时间检查和保持时间检查因此必须找到一种准确而便捷的方法来求取该路径。

在本文中将选择性的就上面多个问题中的一部分进行讨论这些问题是：

数字集成电路的静态时序分析（第二章）

时序分析中的相关文件和架构（第三章）

互连线的时延估算 （第四章）

关键路径方法 （第五章）

考虑串扰效应的静态时序分析（第六章）

 

第二章 数字集成电路的静态时序分析[微软中国1]

静态时序分析是大规模集成电路设计中非常重要的一个方面。在电路设计过程中，为得到一个最佳的电路设计，在结构逻辑、电路布局布线等方面时序分析起着关键性的作用。静态时序分析既要检验电路的最大延迟以保证电路在指定的频率下能够满足建立时间的要求； 同时又要检验电路的最小延迟以满足保持时间的需求。芯片的设计只有通过了静态时序分析才能真正完成甚至在从逻辑综合开始后的每一个步骤的结果都需要满足或部分满足时序的要求。

随着芯片尺寸的减小和集成度密集化的增强、电路设计复杂度的增加、电路性能要求的提高等，新的变化都对芯片内的时序分析提出了更高的要求。

2.1 数字集成电路中的时序问题

在一个同步时序电路中, 所有的触发器都由一个共同的外部时钟线控制,这条时钟线通常称为全局时钟(global clock)。为了实现严格的同步, 电路中的时序关系必须满足一定的条件。

2.1.1 建立时间和保持时间

一个下降沿触发的触发器，它有3个端口，即数据输入端(data input)、数据输出端(data output)和控制端(control input)。它的基本工作原理是：当控制端口由高电平变化为低电平时触发器对数据输入端进行采样，并把采样值送到数据输出端。当控制端口为其它情况时数据输出端维持原采样值。直至控制端口第二次由高电平变化为低电平它的时序关系如图2-1 所示：

实际上由于物理元器件本身的特性,为了保证采样过程的准确，数据输入端必须在实际采样时间到达之前就保持稳定，同样在采样时间之后数据输入端仍然必须维持一段时间。这其实就是通常所说的数据输入端相对于采样时刻的数据建立时间(setup time) 和数据保持时间(hold time) 。如上图所示当触发器类型确定以后建立时间和保持时间由该触发器本身的结构决定,一般来说它们是常数。

图2-1 建立时间和保持时间

2.1.2 时钟偏斜(clock skew)

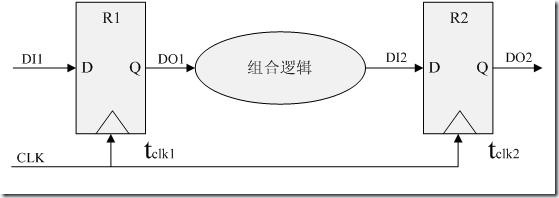
在一个典型的同步时序电路中触发器的数据输入端连接到一个组合逻辑电路的输出，而该组合逻辑电路的输入又连接到一些触发器的数据输出端。如图2-2所示：

图2-2 同步时序电路

从以上的同步时序电路上可以看到时钟到达R1 和R2 的时间Tclk1 和Tclk2 很可能是有差异的我们把时钟到达不同触发器的时间差定义为时钟偏斜（clock

Skew）用δ表示。公式为：

δ = Tclk1 – Tclk2 （2-1）

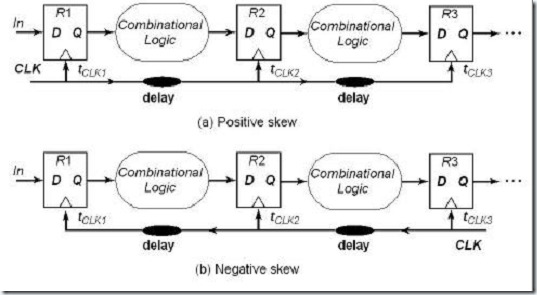
时钟skew 在不同的时钟布线的情况下可正可负，如图2-3：

图2-3 时钟偏斜

时钟skew的正负这样定义,当时钟信号的传输方向和逻辑信号的传输方向一致时,skew为正如图2-3(a)。当时钟信号的传输方向和逻辑信号的传输方向相反时，skew为负如图2-3(b)。

2.1.3 时延约束

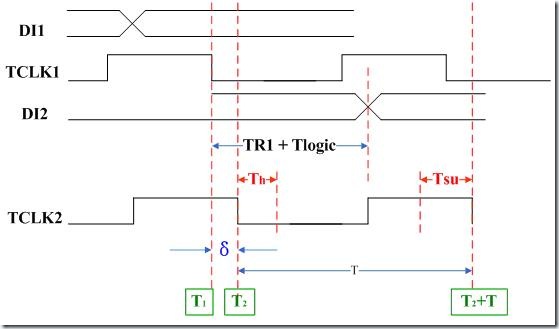
自制图片（下文可参考）

(1) 建立时间约束

由前面对的分析知道,为了实现正确的同步,触发器的数据输入端必须满足建立时间的要求。图2-2中，触发器R1在时钟信号到达R1后输出逻辑信号，输出的逻辑信号在经过组合逻辑电路后到达触发器R2。逻辑信号达到R2的时刻应该比下一个周期时钟信号到达R2的时刻至少早一个建立时间的长度。用公式表示为：

(T2 + T) - (T1 + tR1 + tlogic) > tsetup （2-2）

式中T1 是本周期时钟信号到达R1的时刻，T2 是本周期时钟信号达到R2 的时刻，T是时钟周期，那么T2 + T是下一个周期的时钟信号到达R2的时刻。

tR1[微软中国2] 是R1中时钟到达后直到Q 端信号输出的延时 tlogic 是逻辑信号在组合逻辑电路中的延时，则 tR1 + tlogic 是逻辑信号从R1到R2的总延时。那么T1 + tR1 + tlogic 是R1输出信号到达R2的时刻。tsetup是建立时间，由于时钟偏斜δ= T2 -T1经过整理得到：

tlogic < T - tR1 - tsetup +δ （2-3）[微软中国3]

则：

T > tlogic + tR1 + tsetup - δ （2-4）

从上式可以看到集成电路的时钟周期受到的约束。研发人员希望芯片的时钟周期越小越好，这样可以提高芯片的频率，但是时钟周期受到了上式的限制。可以看到要缩短时钟周期就要减小组合逻辑和时序逻辑的延时，从另一个方面也说明了静态时序分析的重要性。

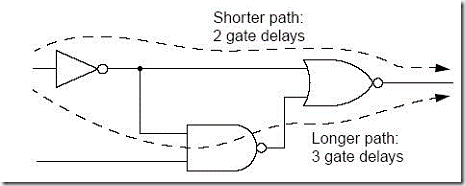
在实际电路中组合逻辑延时并不是固定值会跟据信号走过的路径不同而改

变如图2-9。在上2-4式中由于大于号在tlogic (组合逻辑延时)的左边为了在各种情况下都使该式成立。所以这里的tlogic是最长的组合逻辑延时是tlogicmax，也就是说从所有只经过组合逻辑连接到R2 的触发器出发找出一条延时最长的路径这条路径的时延必须满足R2的建立时间时延约束。

由于类似2-4式在集成电路中的所有有信号传播关系的时序逻辑单元之间都要满足由于tR1、tsetup、及δ相对tlogicmax很小，因而在所有每两个时序逻辑单元之间的这样的最大路径中时延最大的一条就是限制时钟周期的最关键因素，我们一般称为“关键路径”。因此找出各个触发器间组合逻辑的最长路径成为静态时序分析工具需要解决的主要问题之一，有关关键路径的查找问题见第4章。

[微软中国4]

图2-9 不同的内部路径

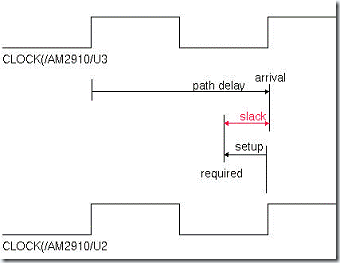
在时序分析工具中把自前级触发器出发的时钟[微软中国5] 到达后级触发器的时间称为“到达时间arrival time”，而把后一级触发器由于setuptime 的原因要求前级信号到达的时间成为“要求时间required time”。

这样把（2-3）变形为：

T +δ- tsetup < tR1 + tlogic （2-5）

其中等式左边就是要求时间 required time：

TR = T +δ- tsetup （2-6）

等式右边边就是到达时间 arrival time：

TA = tR1 + tlogic （2-7）

则TR > TA，而一般把TR - TA的值称作slack，用来表明该时序路径上是否有违反建立时间约束的情况。当slack为正值时表明满足建立时间约束，当slack为负则不满足建立时间约束。对于不满足时序约束的情况称为timing violation

下图就是一个slack为负出现setup timing violation的例子：

图2-4 违反建立时延约束情况timing violation

(2) 保持时间约束

从前面对保持时间的定义中可以知道在时钟信号到达触发器并对触发器输入端采样之后，数据输入端仍然必须维持一段时间才能保证触发器输出端的正确输出。

由于一般情况下，后级触发器在本时钟边沿收到的前级触发器在上一个时钟边沿处发出的信号。所以为了保证后级触发器上本周期时钟到达后仍稳定一段时间前级触发器在本时钟边沿发出的信号到达后级触发器的时间不能太早，前级触发器本时钟沿的输出信号应当在后级触发器本时钟沿到达后经过保持时间后才到达后级触发器。用公式表示为：

T1 + tR1 + tlogic > T2 + Thold (2-8)[微软中国6]

式中左边的T1 + tR1 + tlogic 是R1输出信号到达R2的时刻,右边为本周期时钟到达R2的时刻加上一个保持时间，经过整理可以得到：

δ < tR1 + tlogic [微软中国7] - Thold (2-9)

从上式中可以看到当δ为正时它一定要小于tR1 + tlogic - Thold ，而当δ 为负时 T > tlogic + tR1 + tsetup - δ，负值δ会引起时钟周期变大而影响芯片性能。所以在集成电路设计中总是希望使同一时钟信号到达所有时序逻辑的时间一致，使δ尽可能的接近零，这样就可以避免上述问题。

在保持时间约束的检查中到达时间为：

TA = tR1 + tlogic

而要求时间为

TR =δ + Thold

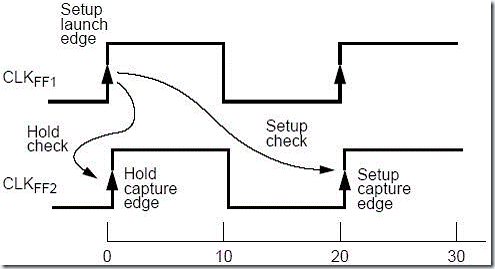
这里要求TA > TR 。另外需要强调的是，一般情况下建立时间是在下一个时钟钟边沿处比较，而保持时间是与两个触发器的同一个时钟边沿之比较。如下图所示：

图2-5 建立时间检查和保持时间检查

由于保持时间时延约束关心的是触发器的当前输入信号稳定保持一段时间。强调输入端的下一个信号的到达不能早于这段时间。这就使得tlogic的定义与其在建立时间约束有明显的不同。这里的tlogic指的是输入端变化最早到达的时间而不是输入端信号的最迟到达的时间。所以这里的tlogic是最快情况下的组合逻辑时延是ltlogicmin。与建立时间时延约束要求寻找最长路径不同这里要寻找最短路径一个数字集成电路要满足其时钟频率正常工作就必须满足以上两个约束而对建立时间和保持时间约束进行检查的方法称为“时序分析”。

---

[微软中国1]静态时序分析与综合的关系，综合工具是怎样进行静态时序分析的？综合时的时序约束与静态时序分析的关系?

[微软中国2]Tco 时间，第一章中的dmax包括Tco和Tlogic。

[微软中国3]不考虑时钟偏斜的情况下，最小的时钟周期 Tmin = Tco + Tlogic + Tsetup。即T > Tco + Tlogic + Tsetup。算上skew后变为：T +δ> Tco + Tlogic + Tsetup

[微软中国4]前后各是一个寄存器，两个寄存器之间可能有n条组合逻辑的路径。其中延时最大的为关键路径。

[微软中国5]应该为数据输出信号把？

[微软中国6]

tR1 + tlogic >δ + Thold

[微软中国7]

Tlogicmin