HDU-1402 A * B Problem Plus FFT(快速傅立叶变化)
题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1402
一般的的大数乘法都是直接模拟乘法演算过程，复杂度O(n^2)，对于这题来说会超时。乘法的过程基本就是等同于多项式相乘的过程，只是没有进位而已。对于这种问题我们需要转化然后用FFT求解。FFT是用来计算离散傅里叶变化(DFT)及其逆变换(IDFT)的快速算法，复杂度O(n*logn)。DFT有一个很重要的性质：时域卷积，频域乘积；频域乘积，时域卷积。那么什么是时域、频域、卷积、乘积呢？时域和频域是两种信号的分析方法，DFT可以把时域信号变化为频域信号。卷积就是作多项式乘法，乘积就是依次乘过去。如果单纯的用多项式表示法进行乘法运算，那么基本就没有优化的地方了，此时我们换一种多项式的表示方法：点值法。表示的就是n个“点-值”对的序列{(x0,y0),(x1,y1),...,(xn-1,yn-1)}，yk满足yk=A(xk)，A()多项式函数，其中xk的值是随便取的。点值法非常适合作乘法，只需要把对应位置的值乘起来就可以了，复杂度O(n)，其实就是做一次乘积，前面的多项式是做一次卷积。那么我们的重点就是怎样快速的把多项式转换为“点值”表示法，如果单纯的带值进去，那么复杂度就是O(n^2)，这个时候FFT就派上用场了，可以在O(n*logn)的时间内求出来。
FFT用到了单位复根的概念，n次单位复根就是满足w^n=1的复数，n次单位复根刚好有n个：e^(2*PI*i*k/n),k=0,1,...,n-1，其中有e^(i*u)=cos(u)+i*sin(u)。n次单位复根有如下的一些引理：
1.相消引理：对于任何整数n>=0,k>=0,d>0,有 
。
2.折半引理：如果n>0为偶数，n个n次的单位复根的平方等于n/2个n/2次单位复根。公式表示为：
。
FFT主要是用到了折半引理，对多项式进行分治运算，它用A(x)中偶数下标的系数与奇数下标的系数，分别定义了两个新的次数为n/2的多项式A[0](x)和A[1](x)：
A[0](x) = a0 + a2x + a4x^4 + ... +an-2x^(n/2-1)
A[1](x) = a1 + a3x + a5x^4 + ... +an-1x^(n/2-1)
那么A(x) = A[0](x^2) + xA[1](x^2)。
我们把点值法中x0,x1,...,xn-1的值分别设为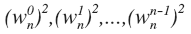
，根据折半引理，值的序列并不是由n个不同的值组成的，而是由n/2个n/2次单位复根所组成，每个根出现两次，那么我们就可以对表达式递归的求值了，复杂度O(nlogn)。把多项式用"点值”法表示的问题解决了，然后做一遍乘积就行了。最后就是把“点值”法求的一个向量f求逆就可以了，对应的过程就是IDFT，思想也是差不多的。。。
FFT算法，网上模板很好找。。。
1 //STATUS:C++_AC_171MS_7128KB 2 #include <functional> 3 #include <algorithm> 4 #include <iostream> 5 //#include <ext/rope> 6 #include <fstream> 7 #include <sstream> 8 #include <iomanip> 9 #include <numeric> 10 #include <cstring> 11 #include <cassert> 12 #include <cstdio> 13 #include <string> 14 #include <vector> 15 #include <bitset> 16 #include <queue> 17 #include <stack> 18 #include <cmath> 19 #include <ctime> 20 #include <list> 21 #include <set> 22 #include <map> 23 using namespace std; 24 //#pragma comment(linker,"/STACK:102400000,102400000") 25 //using namespace __gnu_cxx; 26 //define 27 #define pii pair<int,int> 28 #define mem(a,b) memset(a,b,sizeof(a)) 29 #define lson l,mid,rt<<1 30 #define rson mid+1,r,rt<<1|1 31 #define PI acos(-1.0) 32 //typedef 33 typedef __int64 LL; 34 typedef unsigned __int64 ULL; 35 //const 36 const int N=200010; 37 const int INF=0x3f3f3f3f; 38 const int MOD=10007,STA=8000010; 39 const LL LNF=1LL<<55; 40 const double EPS=1e-4; 41 const double OO=1e30; 42 const int dx[4]={-1,0,1,0}; 43 const int dy[4]={0,1,0,-1}; 44 const int day[13]={0,31,28,31,30,31,30,31,31,30,31,30,31}; 45 //Daily Use ... 46 inline int sign(double x){return (x>EPS)-(x<-EPS);} 47 template<class T> T gcd(T a,T b){return b?gcd(b,a%b):a;} 48 template<class T> T lcm(T a,T b){return a/gcd(a,b)*b;} 49 template<class T> inline T lcm(T a,T b,T d){return a/d*b;} 50 template<class T> inline T Min(T a,T b){return a<b?a:b;} 51 template<class T> inline T Max(T a,T b){return a>b?a:b;} 52 template<class T> inline T Min(T a,T b,T c){return min(min(a, b),c);} 53 template<class T> inline T Max(T a,T b,T c){return max(max(a, b),c);} 54 template<class T> inline T Min(T a,T b,T c,T d){return min(min(a, b),min(c,d));} 55 template<class T> inline T Max(T a,T b,T c,T d){return max(max(a, b),max(c,d));} 56 //End 57 //复数结构体 58 struct complex 59 { 60 double r,i; 61 complex(double _r = 0.0,double _i = 0.0) 62 { 63 r = _r; i = _i; 64 } 65 complex operator +(const complex &b) 66 { 67 return complex(r+b.r,i+b.i); 68 } 69 complex operator -(const complex &b) 70 { 71 return complex(r-b.r,i-b.i); 72 } 73 complex operator *(const complex &b) 74 { 75 return complex(r*b.r-i*b.i,r*b.i+i*b.r); 76 } 77 }; 78 /* 79 * 进行FFT和IFFT前的反转变换。 80 * 位置i和 （i二进制反转后位置）互换 81 * len必须去2的幂 82 */ 83 void change(complex y[],int len) 84 { 85 int i,j,k; 86 for(i = 1, j = len/2;i < len-1; i++) 87 { 88 if(i < j)swap(y[i],y[j]); 89 //交换互为小标反转的元素，i<j保证交换一次 90 //i做正常的+1，j左反转类型的+1,始终保持i和j是反转的 91 k = len/2; 92 while( j >= k) 93 { 94 j -= k; 95 k /= 2; 96 } 97 if(j < k) j += k; 98 } 99 } 100 /* 101 * 做FFT 102 * len必须为2^k形式， 103 * on==1时是DFT，on==-1时是IDFT 104 */ 105 void FFT(complex y[],int len,int on) 106 { 107 change(y,len); 108 for(int h = 2; h <= len; h <<= 1) 109 { 110 complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h)); 111 for(int j = 0;j < len;j+=h) 112 { 113 complex w(1,0); 114 for(int k = j;k < j+h/2;k++) 115 { 116 complex u = y[k]; 117 complex t = w*y[k+h/2]; 118 y[k] = u+t; 119 y[k+h/2] = u-t; 120 w = w*wn; 121 } 122 } 123 } 124 if(on == -1) 125 for(int i = 0;i < len;i++) 126 y[i].r /= len; 127 } 128 129 char s1[N],s2[N]; 130 int ans[N]; 131 complex a[N],b[N]; 132 133 int main(){ 134 // freopen("in.txt","r",stdin); 135 int i,j,len1,len2,len; 136 while(~scanf("%s%s",s1,s2)) 137 { 138 len1=strlen(s1); 139 len2=strlen(s2); 140 len=1; 141 while(len<(len1<<1) || len<(len2<<1))len<<=1; 142 for(i=0;i<len1;i++)a[i]=complex(s1[len1-i-1]-'0',0); 143 for(;i<len;i++)a[i]=complex(0,0); 144 for(i=0;i<len2;i++)b[i]=complex(s2[len2-i-1]-'0',0); 145 for(;i<len;i++)b[i]=complex(0,0); 146 147 FFT(a,len,1); 148 FFT(b,len,1); 149 for(i=0;i<len;i++)a[i]=a[i]*b[i]; 150 FFT(a,len,-1); 151 for(i=0;i<len;i++)ans[i]=(int)(a[i].r+0.5); 152 len=len1+len2-1; 153 for(i=0;i<len;i++){ 154 ans[i+1]+=ans[i]/10; 155 ans[i]%=10; 156 } 157 for(i=len;ans[i]<=0 && i>0;i--); 158 for(;i>=0;i--) 159 printf("%d",ans[i]); 160 putchar('\n'); 161 } 162 return 0; 163 }
