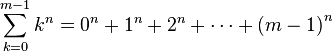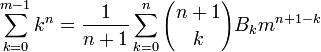POJ-1707 Sum of powers bernoulli方程

　　题目链接：http://poj.org/problem?id=1707

　　利用bernoulli方程来解决此题。

     数学上，伯努利数Bn的第一次发现是与下述数列和的公式有关：

        \sum_{k=0}^{m-1} k^n = 0^n + 1^n + 2^n + \cdots + {(m-1)}^n

     其中n为固定的任意正整数。

     这数列和的公式必定是变量为m，次数为n+1的多项式，称为伯努利多项式。伯努利多项式的系数与伯努利数有密切关系如下：

      \sum_{k=0}^{m-1} k^n = {1\over{n+1}}\sum_{k=0}^n{n+1\choose{k}} B_k m^{n+1-k}

     

     举例说，把n取为1，我们有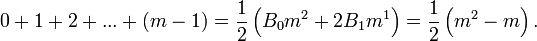 0 + 1 + 2 + ... + (m-1) = \frac{1}{2}\left(B_0 m^2+2B_1 m^1\right) = \frac{1}{2}\left(m^2-m\right).

    伯努利数可以由下列递推公式计算：

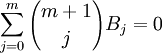    \sum_{j=0}^m{m+1\choose{j}}B_j = 0，初值条件为B0 = 1。     [摘自wikipedia]

     注意:这里计算的是0~m-1的值，因此最后第二项还要加上一个m^n;

 1 //STATUS:C++_AC_0MS_140KB
 2 #include<stdio.h>
 3 #include<stdlib.h>
 4 #include<string.h>
 5 #include<math.h>
 6 #include<iostream>
 7 #include<string>
 8 #include<algorithm>
 9 #include<vector>
10 #include<queue>
11 #include<stack>
12 #include<map>
13 using namespace std;
14 #define LL __int64
15 #define pii pair<int,int>
16 #define Max(a,b) ((a)>(b)?(a):(b))
17 #define Min(a,b) ((a)<(b)?(a):(b))
18 #define mem(a,b) memset(a,b,sizeof(a))
19 #define lson l,mid,rt<<1
20 #define rson mid+1,r,rt<<1|1
21 const int N=25,INF=0x3f3f3f3f,MOD=40001,STA=8000010;
22 const double DNF=1e13;
23 
24 LL B[N][2],C[N][N],f[N][2];
25 int n,m;
26 
27 
28 LL gcd(LL a,LL b){return b?gcd(b,a%b):a;}
29 LL lcm(LL a,LL b){return a/gcd(a,b)*b;}
30 
31 void getC(int n)
32 {
33     int i,j;
34     n++;
35     for(i=0;i<=n;i++)C[i][0]=C[i][i]=1;
36     for(i=2;i<=n;i++){
37         for(j=1;j<n;j++){
38             C[i][j]=C[i-1][j-1]+C[i-1][j];
39         }
40     }
41 }
42 
43 void bernoulli(int n)
44 {
45     int i,m;
46     LL s[2],b[2],l,g;
47     B[0][0]=1;B[0][1]=1;
48     for(m=1;m<=n;m++){
49         s[0]=1,s[1]=1;
50         for(i=1;i<m;i++){
51             b[0]=C[m+1][i]*B[i][0];
52             b[1]=B[i][1];
53             l=lcm(s[1],b[1]);
54             s[0]=l/s[1]*s[0]+l/b[1]*b[0];
55             s[1]=l;
56         }
57         s[0]=-s[0];
58         if(s[0]){
59             g=gcd(s[0],s[1]*C[m+1][m]);
60             B[m][0]=s[0]/g;
61             B[m][1]=s[1]*C[m+1][m]/g;
62         }
63         else B[m][0]=0,B[m][1]=1;
64     }
65 }
66 
67 int main()
68 {
69  //   freopen("in.txt","r",stdin);
70     int i,j;
71     LL g,maxlcm;
72     getC(20);
73     bernoulli(20);
74     while(~scanf("%d",&m))
75     {
76         for(i=0;i<=m;i++){
77             g=gcd(C[m+1][i],B[i][1]);
78             f[i][0]=C[m+1][i]/g*B[i][0];
79             f[i][1]=B[i][1]/g;
80         }
81         maxlcm=f[0][1];
82         for(i=1;i<=m;i++){
83             maxlcm=lcm(maxlcm,f[i][1]);
84         }
85         if(maxlcm<0)maxlcm=-maxlcm;
86         for(i=0;i<=m;i++){
87             f[i][0]*=maxlcm/f[i][1];
88         }
89         f[1][0]+=maxlcm*(m+1);
90 
91         printf("%I64d",(m+1)*maxlcm);
92         for(i=0;i<=m;i++)
93             printf(" %I64d",f[i][0]);
94         printf(" 0\n");
95     }
96     return 0;
97 }
posted @ 2013-04-08 23:25  zhsl  阅读(604)  评论(0)  编辑  收藏  举报