首尾相连一维数组的最大子数组和

设计思想： 

因为已经写过了一维数组的求最大子数组的程序，所以在原基础上做一些修改就可以了。与求数组的最大子数组相同，先遍历所有子数组，然后判断最后一个子数组是否大于0。若大于0，则重头开始遍历，直到子数组的和小于0或者到最后一个子数组的前一个数为止，在此过程中保存子数组的最大值以及位置。在此需要注意的是，如果不加限制条件，求出的最大子数组可能会超过原数组的长度。我用了一个限制条件，一旦长度等于原长度，就跳出循环。

源程序代码：

#include<stdio.h>

#include<stdlib.h>

int maxSumNoConnect(int*arr,int n)

{

    int i,max,*sum;

    sum=(int *)malloc(sizeof(int)*n);

    sum[0]=max=arr[0];

    for (i=1;i<n;i++){

     if(sum[i-1]>0)

        sum[i]=arr[i]+sum[i-1];

     else

        sum[i]=arr[i];

     if(sum[i]>max) max=sum[i];
}
 
free(sum);

return max;

}

int indexInArrMinSum(int*arr,int n)

{

int i,loc,min,*sum;

sum=(int*)malloc(sizeof(int)*n);

min=sum[0]=arr[0];

loc=0;

for(i=1;i<n;i++){

 if (sum[i-1]>0){

    sum[i]=arr[i];

}else{

    sum[i]=arr[i]+sum[i-1];

}

if (sum[i]<min){

    loc=i;

    min=sum[i];

 }

}

free(sum);

return loc;

}

int maxSumConnect(int*arr,int n)

{

 int index,i,loc,cur,max,*sum;

 sum=(int*)malloc(sizeof(int)*n);

 index=indexInArrMinSum(arr,n);

 max=sum[(index+1)%n]=arr[(index+1)%n];

 for(i=2;i<n;i++){

 loc=(index+i-1)%n;

 cur=(index+i)%n;

if (sum[loc]>0){

    sum[cur]=arr[cur]+sum[loc];

}else{

    sum[cur]=arr[cur];

}

 if(sum[cur]>max)

    max=sum[cur];

}

 free(sum);

 return max;

}

int main(void)

{

 int i,n,flag,conn_n,conn_y,*arr;

 while(scanf("%d",&n)!=EOF){

 arr=(int*)malloc(sizeof(int)*n);

 for(i=0,flag=0;i<n;i++){

    scanf("%d",arr+i);

    if (*(arr+i)<=0)

     flag++;

}

if (flag==n){

    printf("0\n");

    continue;

}

 conn_n=maxSumNoConnect(arr,n);

 conn_y=maxSumConnect(arr,n);

 if (conn_n<conn_y)

    printf("%d\n",conn_y);

 else

    printf("%d\n",conn_n);

 free(arr);

 }

 return 0;

}

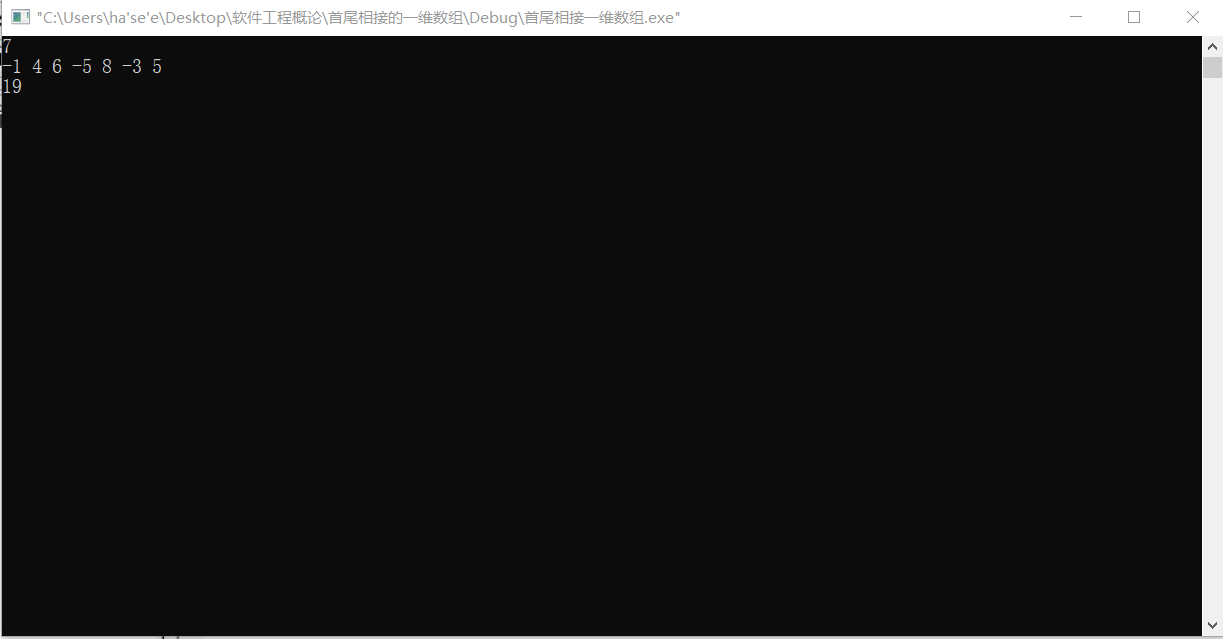
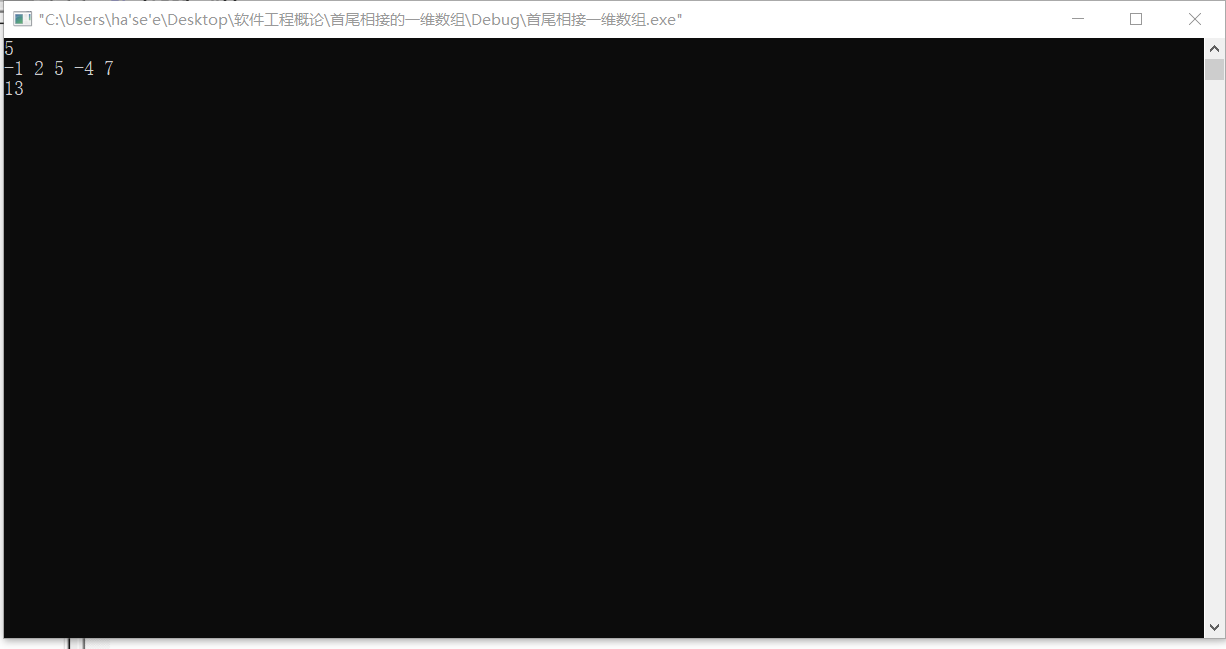
运行结果截图：（需要自己输入一个一维数组，第一行是数组中元素个数，第二行是各个元素）

 

编码、调试：张洪胜