Luogu P4425 转盘 题解 [ 黑 ] [ 线段树 ] [ 贪心 ] [ 递归 ]
转盘：蒟蒻的第一道黑，这题是贪心和线段树递归合并的综合题。
贪心
破环成链的 trick 自然不用多说。
首先观察题目，很容易发现一个性质：只走一圈的方案一定最优。这个很容易证，因为再绕一圈回来标记前面的和等前面的标记完之后继续走是等价的，并且再绕一圈甚至可能更劣。
于是，我们只用走一圈，并且在走路的途中走走停停，就可以走出最优解。
但这依然不怎么好求，通过观察发现：我们把所有停下的时间移到前面来，在起点就把要停的时间全部停掉，和走走停停是等价的，并且这样更好求。
接下来我们就来推式子了：
假设当前的时间是 \(t\)，我们从 \(i\) 出发，要走到 \(j\) 处，并且 \(j\) 处的最早出现时间为 \(a_j\)，那么可以列出方程：
移项得：
因此在此时 \(t\) 的最小值就是 \(\max_{j=i}^{i+n-1}(a_j-j+i)\)。
由于每次走路还要计算时间，所以总时间为 \(\max_{j=i}^{i+n-1}(a_j-j+i)+n-1\)。
因为要最小化，所以答案就是 \(\min_{i=1}^{n}(\max_{j=i}^{i+n-1}(a_j-j+i))+n-1\)。
线段树与递归
根据上面的分析，我们需要维护 \(\min_{i=1}^{n}(\max_{j=i}^{i+n-1}(a_j-j+i))+n-1\) 这个式子。
首先 \(\max_{j=i}^{i+n-1}(a_j-j+i)\) 是很好维护的，我们可以通过一个线段树来维护。
但是外面的那个 \(\min_{i=1}^{n}\) 怎么维护？实际上我们可以通过在线段树上递归来实现。
设 \(x\) 表示线段树上某个节点的最小值。因为我们只需要求出起点在 \(1\) 到 \(n\) 中的最小值（后面一部分是复制两倍后的，所以和前面的重复了，可以不要计算），所以 \(x\) 就是这个节点左半部分的最小值，而不是整个节点的最小值。但也不是说按整个节点算就不可以了，只是说这样做代码好写、思路好想一些。
接下来考虑如何递归合并信息：
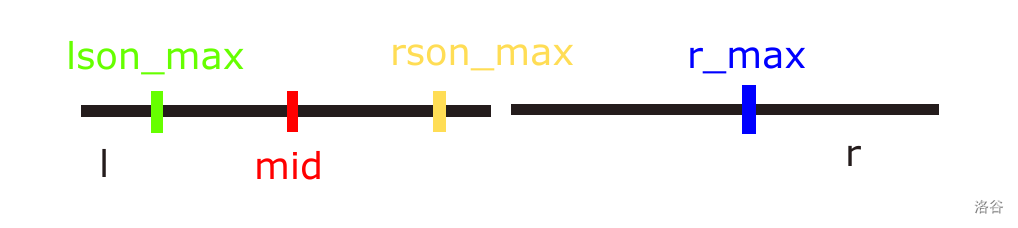
注意：当前我们处在的节点是 \(l\)。
当递归到叶子节点时
由式子可知，直接返回 \(i+\max(lson_{max},r_{max})\) 即可。
当 \(rson_{max}< r_{max}\) 时
\(r_{max}\) 依然是最大值，所以要接下来递归 \(l\) 的左儿子 \(lson\)，因为右儿子已经确定贡献了，贡献就是 \(\min(dfs(lson,r_{max}),mid+1+r_{max})\)。
当 \(rson_{max}\ge r_{max}\) 时
\(rson_{max}\) 把 \(r_{max}\) 挤下去了，所以要接下来递归 \(l\) 的右儿子 \(rson\)，以找到右儿子的那个最大值在哪，才能确定贡献，左儿子的贡献就是 \(\min(x_l,dfs(rson,r_{max}))\)。
注意 \(x_l\) 与 \(dfs(p,r_{max})\) 函数的定义不同，其一是表示左半部分的最小值，另一个是表示全部区间的最小值。
其余部分就是按照线段树常规的配置来写了。
代码
#include <bits/stdc++.h>
#define fi first
#define se second
#define lc (p<<1)
#define rc ((p<<1)|1)
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
const int N=200005;
int n,m,q,a[N],lastans=0;
struct node{
int l,r;
int mx,mi;
}tr[4*N];
int dfs(int p,int mxr)
{
if(tr[p].l==tr[p].r)return (tr[p].l+max(mxr,tr[p].mx));
int mid=(tr[p].l+tr[p].r)>>1;
if(tr[rc].mx<mxr)return min(dfs(lc,mxr),mid+1+mxr);
return min(tr[p].mi,dfs(rc,mxr));
}
void pushup(int p)
{
tr[p].mx=max(tr[lc].mx,tr[rc].mx);
tr[p].mi=dfs(lc,tr[rc].mx);
}
void build(int p,int ln,int rn)
{
tr[p]={ln,rn,a[ln]-ln,ln+a[ln]-ln};
if(ln==rn)return;
int mid=(ln+rn)>>1;
build(lc,ln,mid);
build(rc,mid+1,rn);
pushup(p);
}
void update(int p,int x,int v)
{
if(tr[p].l==x&&tr[p].r==x)
{
tr[p].mx=v-x;
tr[p].mi=x+v-x;
return;
}
int mid=(tr[p].l+tr[p].r)>>1;
if(x<=mid)update(lc,x,v);
else update(rc,x,v);
pushup(p);
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m>>q;
for(int i=1;i<=n;i++)cin>>a[i],a[i+n]=a[i];
build(1,1,2*n);
cout<<tr[1].mi+n-1<<endl;
lastans=tr[1].mi+n-1;
while(m--)
{
int x,y;
cin>>x>>y;
if(q)x^=lastans,y^=lastans;
update(1,x,y);
update(1,x+n,y);
cout<<tr[1].mi+n-1<<endl;
lastans=tr[1].mi+n-1;
}
return 0;
}
