图论杂项小技巧
该 blog 持续更新。
1.虚点
虚点，是指在图中创建一个不存在的源点，把这个源点和其他的一些点连接起来（可以全连，也可以只连一部分；边权可以为 0 ，也可以不为 0 。），通常作用为：
- 把所有点加入同一个连通图中，如 SPFA 判断负环创建一个边权为 0 的虚点 （SPFA判负环）。
- 处理自环的边权，如下文中例题：买票（最小生成树建虚点例题）。
(1) SPFA判负环
题面
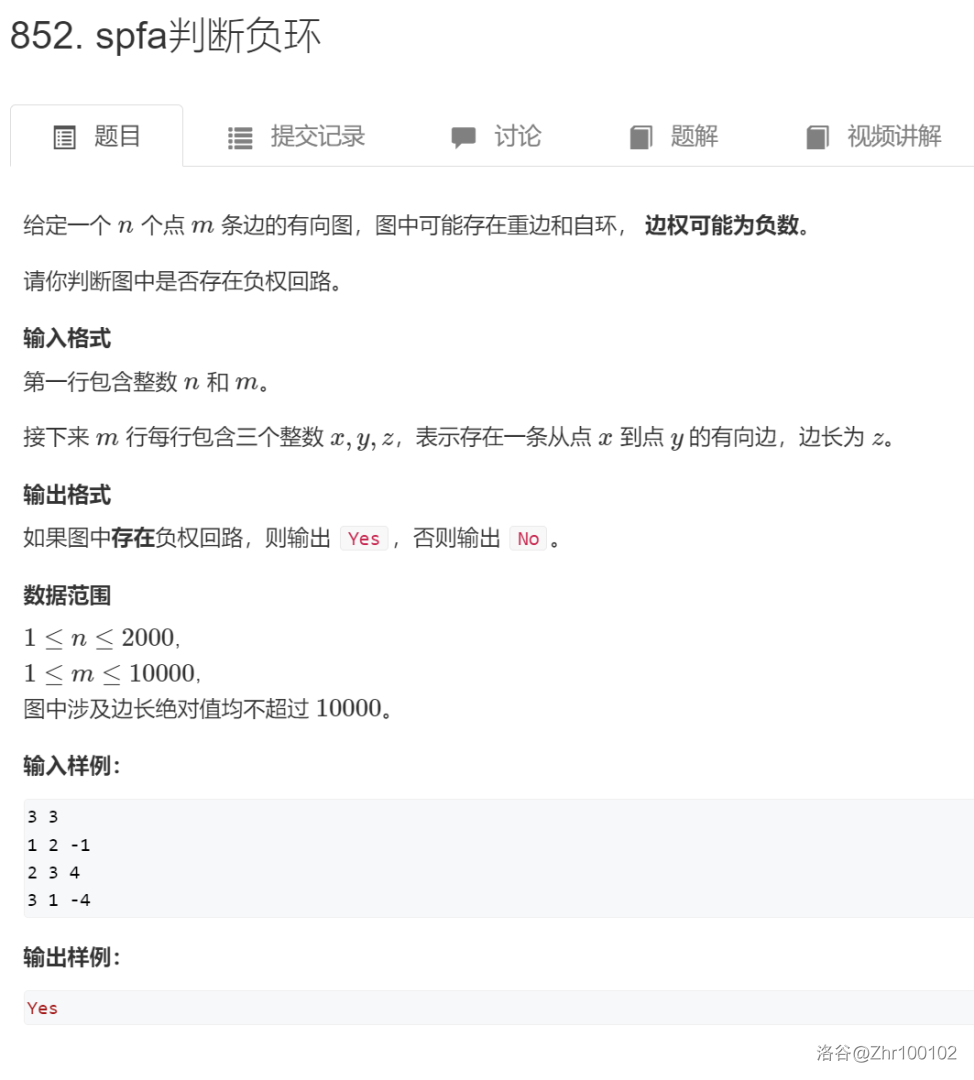
题解
初始化 SPFA 时将所有节点加入 queue 中，就相当于创建了一个虚拟源点，与原图中的所有节点连了一条边权为 0 的从虚点指向该点的有向边，然后判断负环。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n,m,x,y,z;
int h[2005],e[10005],ne[10005],w[10005],idx=0;
int dis[2005],cnt[2005];
queue<int> q;
bool inq[2005];
void add(int a,int b,int c)
{
e[++idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx;
}
bool spfa()
{
for(int i=1;i<=n;i++)//虚拟源点的思想，边权为0
{
q.push(i);
inq[i]=1;
}
while(!q.empty())
{
int u=q.front();
q.pop();
inq[u]=0;
for(int i=h[u];i!=-1;i=ne[i])
{
int v=e[i],nw=w[i];
if(dis[u]+nw<dis[v])
{
dis[v]=dis[u]+nw;
cnt[v]=cnt[u]+1;
if(cnt[v]>=n)
{
return 1;
}
if(inq[v]==0)
{
q.push(v);
inq[v]=1;
}
}
}
}
return 0;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
memset(h,-1,sizeof(h));
for(int i=1;i<=m;i++)
{
cin>>x>>y>>z;
add(x,y,z);
}
if(spfa())cout<<"Yes";
else cout<<"No";
return 0;
}
(2) 最小生成树建虚点例题
题面
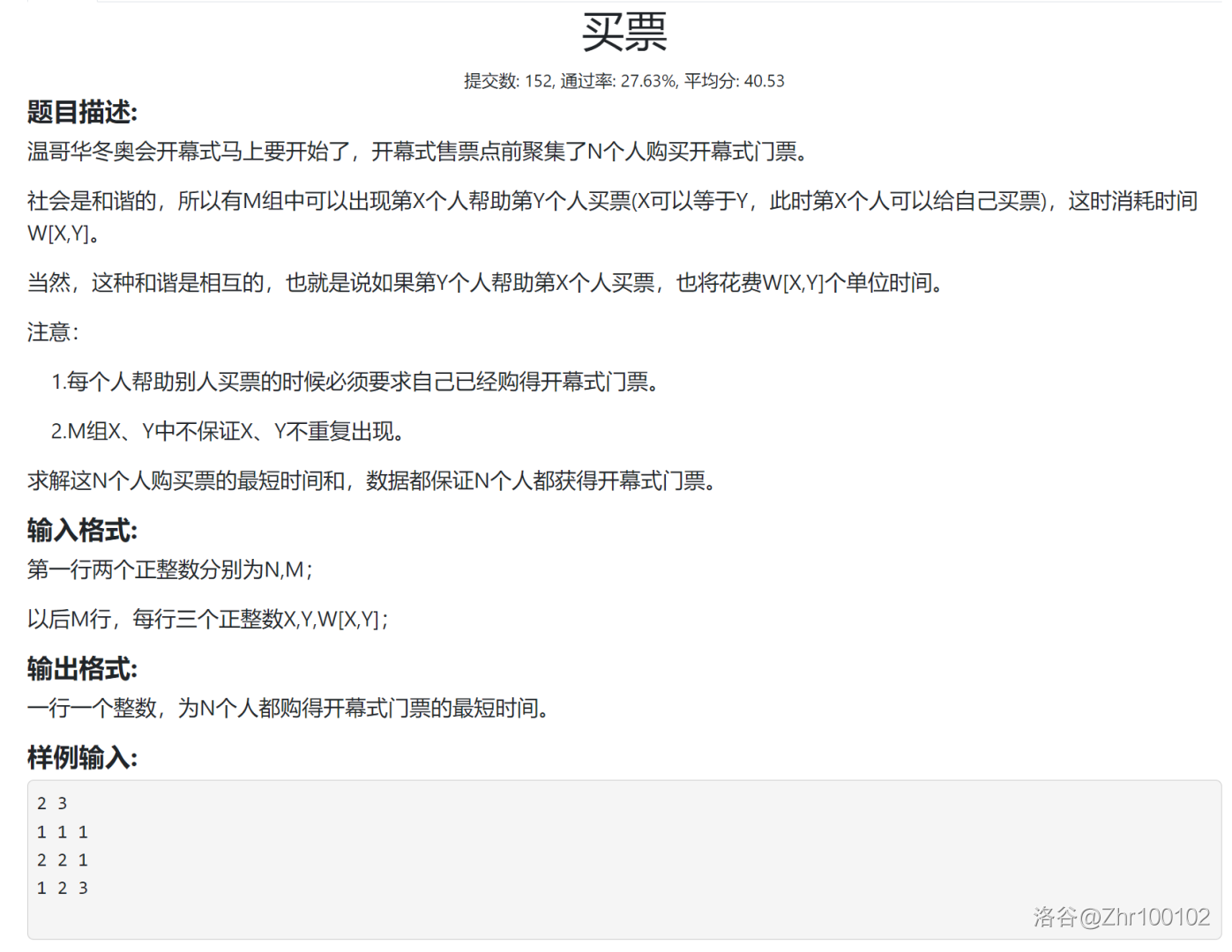
题解
给自己买票相当于给虚拟源点连一条边权为 \(w\) 的边，因为至少要有一个人给自己买票才能给其他人买票，所以就此跑最小生成树即可。本题代码用编号为 0 的点表示虚拟源点。
PS: 本题因为边数较多，实际上用 Prim 算法的时间更优，但下面代码用了 Kruskal 算法。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int n,m,x,y,w,ans=0;
struct edge{
int u,v,w;
};
edge e[4000005];
bool cmp(edge a,edge b)
{
return a.w<b.w;
}
int dsu[2005];
int findf(int a)
{
if(dsu[a]!=a)dsu[a]=findf(dsu[a]);
return dsu[a];
}
void combine(int a,int b)
{
int fa=findf(a),fb=findf(b);
dsu[fa]=fb;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=2000;i++)dsu[i]=i;
for(int i=1;i<=m;i++)
{
cin>>x>>y>>w;
if(x==y)
{
e[i]={0,x,w};
}
else
{
e[i]={x,y,w};
}
}
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++)
{
if(findf(e[i].u)!=findf(e[i].v))
{
combine(e[i].u,e[i].v);
ans+=e[i].w;
}
}
cout<<ans;
return 0;
}
2.反图
反图，是把原图中的所有边的起点 \(u\) 和 终点 \(v\) 全部交换，并保持边权不变后得到的图。
它的使用一般在类似最短路径问题等应用于有向图且所有边倒置后结果不变的算法中。
通常作用为：
- 反着跑最短路，以达到某些限制，如 CSP-J 2023 旅游巴士 中 要求不早于 \(a_i\) 的时间通过某个点，就可以转化为必须在剩余时间大于等于 \(a_i\) 的时间内通过该点，可直接用 Dijkstra 求解（ CSP-J 2023 旅游巴士 ）。
3.二分
4.菊花
5.前 \(k\) 大值
在求某些东西的最大值的时候，只要这个最大值满足最多只能由前 ... 个得到，就可以维护前 \(k\) 大值，进行转移。
6.中转点
枚举中转点，把 3 个点连通。类似最小斯坦纳树。
7.度数分析
尤其是在对环分析的时候。类似基环树，和一切与环有关的东西。
8.逆向分析
对于删除一个点操作，我们可以逆向操作，转化为加点的操作。比较经典的例子是并查集。
to be continued...
