UOJ#397. 【NOI2018】情报中心 线段树合并 虚树
原文链接www.cnblogs.com/zhouzhendong/p/UOJ397.com
前言
这真可做吗?只能贺题解啊……
题解
我们称一条路径的 LCA 为这条路径两端点的 LCA。
我们将相交的路径分成两种:
- 两条路径的 LCA 相同。
- 两条路径的 LCA 不同。
设路径 \(1\) 的两端点为 \(x_1,y_1\),LCA 为 \(lca_1\) ,消耗为 \(v_1\) 。
设路径 \(2\) 的两端点为 \(x_2,y_2\),LCA 为 \(lca_2\) ,消耗为 \(v_2\) 。
设原树上两点带权距离为 \(Dis(x,y)\),一个点的带权深度为 \(len_x\) 。
接下来我们分两种情况讨论一下这个问题。
\(lca_1 \neq lca_2\)
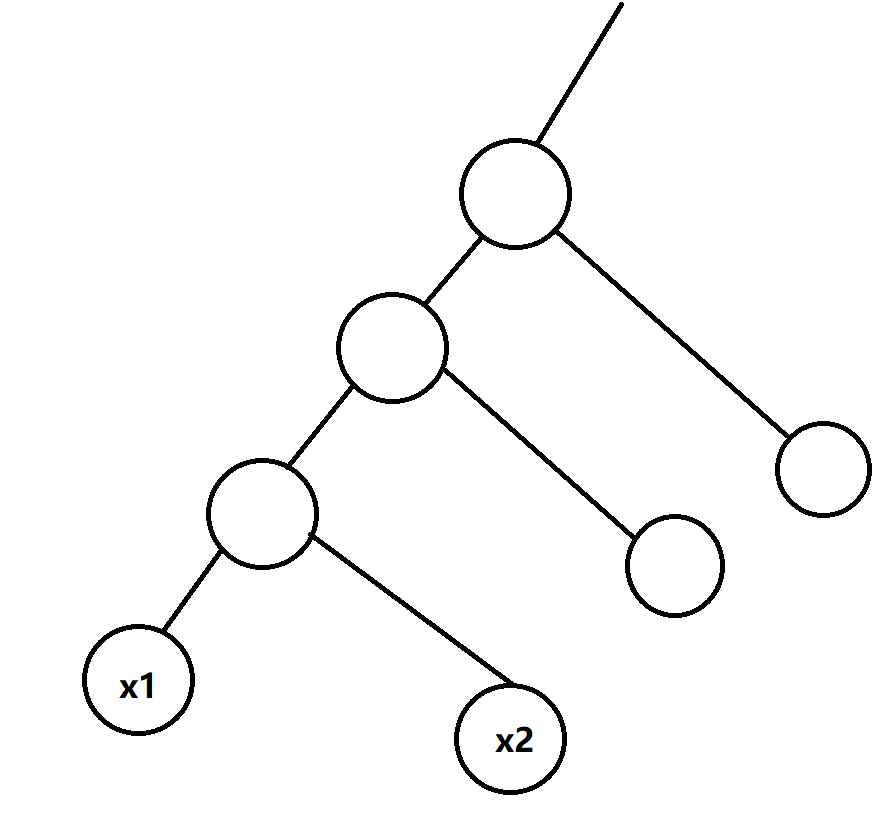
\[ans = Dis(x_1,y_1) + Dis(x_2,y_2) - v_1 - v_2 - len[LCA(x_1,x_2)] + \max(len[lca_1],len[lca_2])
\]
大力线段树合并即可。
\(lca_1 = lca _2 = 1\)
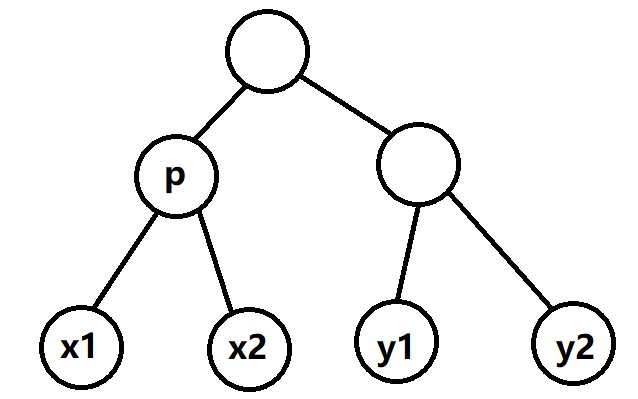
\[ans \times 2 = -2 v_1-2v_2 + Dis(x_1,y_1) + Dis(x_2,y_2) + len[x_1] + len [x_2] + Dis(y_1,y_2) - 2 len[p]
\]
类似于WC2018通道 的做法,我们修改 \(y_1,y_2\) 的深度定义,然后对 \(p\) 进行 dfs,对 \(y_1,y_2\) 维护最远点对即可。
\(lca_1 = lca_2\)
如果 LCA 不恒为 1 ,那么我们只需要枚举 LCA,然后每次建个虚树实现即可。
以上总时间复杂度为 \(O((n+m) \log n)\) 。
代码
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof x)
#define For(i,a,b) for (int i=(a);i<=(b);i++)
#define Fod(i,b,a) for (int i=(b);i>=(a);i--)
#define fi first
#define se second
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
#define outval(x) cerr<<#x" = "<<x<<endl
#define outtag(x) cerr<<"---------------"#x"---------------"<<endl
#define outarr(a,L,R) cerr<<#a"["<<L<<".."<<R<<"] = ";\
For(_x,L,R)cerr<<a[_x]<<" ";cerr<<endl;
using namespace std;
typedef long long LL;
LL read(){
LL x=0,f=0;
char ch=getchar();
while (!isdigit(ch))
f|=ch=='-',ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return f?-x:x;
}
const int N=50005,M=100005;
const LL INF=1e17;
int T,n,m;
struct Graph{
int cnt,y[M],z[M],nxt[M],fst[N];
void clear(int n){
cnt=1,memset(fst,0,(n+5)<<2);
}
void add(int a,int b,int c){
y[++cnt]=b,nxt[cnt]=fst[a],fst[a]=cnt,z[cnt]=c;
}
}g;
int depth[N],fa[N][20];
int I[N],O[N],Time;
LL len[N];
void dfs(int x,int pre,int D,LL L){
I[x]=++Time;
depth[x]=D,len[x]=L,fa[x][0]=pre;
For(i,1,19)
fa[x][i]=fa[fa[x][i-1]][i-1];
for (int i=g.fst[x];i;i=g.nxt[i]){
int y=g.y[i];
if (y!=pre)
dfs(y,x,D+1,L+g.z[i]);
}
O[x]=Time;
}
int LCA(int x,int y){
if (depth[x]<depth[y])
swap(x,y);
Fod(i,19,0)
if (depth[x]-(1<<i)>=depth[y])
x=fa[x][i];
if (x==y)
return x;
Fod(i,19,0)
if (fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
LL Dis(int x,int y){
return len[x]+len[y]-len[LCA(x,y)]*2;
}
LL ans;
struct ch{
int x,y,lca;
LL v,co;
}a[M];
namespace S1{
const int S=M*20*5;
int ls[S],rs[S];
LL mxL[S],mxR[S];
int cnt;
void pushup(int rt){
mxL[rt]=max(mxL[ls[rt]],mxL[rs[rt]]);
mxR[rt]=max(mxR[ls[rt]],mxR[rs[rt]]);
}
void Ins(int &rt,int L,int R,int x,LL vL,LL vR){
if (!rt)
rt=++cnt,ls[rt]=rs[rt]=0,mxL[rt]=mxR[rt]=-INF;
mxL[rt]=max(mxL[rt],vL);
mxR[rt]=max(mxR[rt],vR);
if (L==R)
return;
int mid=(L+R)>>1;
if (x<=mid)
Ins(ls[rt],L,mid,x,vL,vR);
else
Ins(rs[rt],mid+1,R,x,vL,vR);
}
int Del(int rt,int L,int R,int x){
if (!rt)
return 0;
int now=++cnt;
ls[now]=ls[rt],rs[now]=rs[rt];
mxL[now]=mxR[now]=-INF;
if (L==R)
return now;
int mid=(L+R)>>1;
if (x<=mid)
ls[now]=Del(ls[rt],L,mid,x);
else
rs[now]=Del(rs[rt],mid+1,R,x);
pushup(now);
return now;
}
LL Add;
int Merge(int x,int y,int L,int R){
if (!x||!y)
return x|y;
int rt=++cnt;
ls[rt]=rs[rt]=0,mxL[rt]=mxR[rt]=-INF;
if (L==R){
mxL[rt]=max(mxL[x],mxL[y]);
mxR[rt]=max(mxR[x],mxR[y]);
return rt;
}
int mid=(L+R)>>1;
ans=max(ans,Add+max(mxL[ls[x]]+mxR[rs[y]],mxL[ls[y]]+mxR[rs[x]]));
ls[rt]=Merge(ls[x],ls[y],L,mid);
rs[rt]=Merge(rs[x],rs[y],mid+1,R);
pushup(rt);
return rt;
}
vector <int> id[N];
int rt[N];
void dfs(int x,int pre){
for (int i=g.fst[x];i;i=g.nxt[i]){
int y=g.y[i];
if (y!=pre)
dfs(y,x);
}
Add=-len[x];
for (int i : id[x]){
int tmp=0;
Ins(tmp,0,n,depth[a[i].lca],a[i].v,a[i].v+len[a[i].lca]);
rt[x]=Merge(rt[x],tmp,0,n);
}
for (int i=g.fst[x];i;i=g.nxt[i]){
int y=g.y[i];
if (y!=pre){
rt[y]=Del(rt[y],0,n,depth[x]);
rt[x]=Merge(rt[x],rt[y],0,n);
}
}
}
void Solve(){
For(i,1,n)
id[i].clear(),rt[i]=0;
For(i,1,m){
if (a[i].x!=a[i].lca)
id[a[i].x].pb(i);
if (a[i].y!=a[i].lca)
id[a[i].y].pb(i);
}
cnt=0;
mxL[0]=mxR[0]=-INF;
dfs(1,0);
}
}
namespace S2{
LL res;
vector <int> id[N];
int st[N],top;
int vid[M*2],ac;
bool cmpI(int a,int b){
return I[a]<I[b];
}
struct Node{
int x;
LL v;
Node(){}
Node(int _x,LL _v){
x=_x,v=_v;
}
};
vector <Node> vn[N];
typedef pair <Node,Node> PC;
PC pr[N];
LL dis(Node a,Node b){
if (!a.x&&!b.x)
return -(INF<<4);
if (!a.x||!b.x)
return -(INF<<2);
return Dis(a.x,b.x)+a.v+b.v;
}
PC Merge(PC a,PC b,int f,LL Add){
LL v00=dis(a.fi,b.fi);
LL v01=dis(a.fi,b.se);
LL v10=dis(a.se,b.fi);
LL v11=dis(a.se,b.se);
if (f)
res=max(res,max(max(v00,v01),max(v10,v11))+Add);
LL va=dis(a.fi,a.se);
LL vb=dis(b.fi,b.se);
LL mx=max(max(max(v00,v01),max(v10,v11)),max(va,vb));
if (mx==v00)
return mp(a.fi,b.fi);
if (mx==v01)
return mp(a.fi,b.se);
if (mx==v10)
return mp(a.se,b.fi);
if (mx==v11)
return mp(a.se,b.se);
if (mx==va)
return a;
if (mx==vb)
return b;
}
void Solve(int x){
ac=0;
for (int i : id[x])
if (a[i].x!=a[i].y)
vid[++ac]=a[i].x,vid[++ac]=a[i].y;
vid[++ac]=x;
sort(vid+1,vid+ac+1,cmpI);
ac=unique(vid+1,vid+ac+1)-vid-1;
For(i,1,ac)
vn[vid[i]].clear();
for (int i : id[x])
if (a[i].x!=a[i].y){
vn[a[i].x].pb(Node(a[i].y,a[i].v-a[i].co+len[a[i].x]));
vn[a[i].y].pb(Node(a[i].x,a[i].v-a[i].co+len[a[i].y]));
}
top=0;
assert(vid[1]==x);
For(_,1,ac){
int i=vid[_];
pr[i]=mp(Node(0,0),Node(0,0));
while (!vn[i].empty()){
pr[i]=Merge(pr[i],mp(vn[i].back(),Node(0,0)),i!=x,-len[i]*2);
vn[i].pop_back();
}
if (top){
int lca=LCA(i,st[top]);
while (depth[st[top]]>depth[lca]){
int id=st[top];
if (depth[st[top-1]]>=depth[lca])
pr[st[top-1]]=Merge(pr[st[top-1]],pr[id],st[top-1]!=x,-len[st[top-1]]*2),top--;
else
pr[lca]=pr[id],st[top]=lca;
}
}
st[++top]=i;
}
while (top>1){
int id=st[top];
pr[st[top-1]]=Merge(pr[st[top-1]],pr[id],st[top-1]!=x,-len[st[top-1]]*2);
top--;
}
}
void dfs(int x,int pre){
for (int i=g.fst[x];i;i=g.nxt[i]){
int y=g.y[i];
if (y!=pre)
dfs(y,x);
}
Solve(x);
}
void Solve(){
For(i,1,n)
id[i].clear();
For(i,1,m)
id[a[i].lca].pb(i);
res=-INF*2;
dfs(1,0);
ans=max(ans,res/2);
}
}
void Solve(){
n=read();
g.clear(n);
For(i,1,n-1){
int a=read(),b=read(),c=read();
g.add(a,b,c),g.add(b,a,c);
}
Time=0;
dfs(1,0,0,0);
m=read();
For(i,1,m){
a[i].x=read(),a[i].y=read(),a[i].co=read();
a[i].v=Dis(a[i].x,a[i].y)-a[i].co;
a[i].lca=LCA(a[i].x,a[i].y);
}
ans=-INF/2;
S1::Solve();
S2::Solve();
if (ans==-INF/2)
puts("F");
else
printf("%lld\n",ans);
}
int main(){
#ifdef zzd
freopen("x.in","r",stdin);
#endif
T=read();
while (T--)
Solve();
return 0;
}

