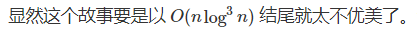UOJ#23. 【UR #1】跳蚤国王下江南 仙人掌 Tarjan 点双 圆方树 点分治 多项式 FFT

原文链接https://www.cnblogs.com/zhouzhendong/p/UOJ23.html

题目传送门 - UOJ#23

题意

　　给定一个有 n 个节点的仙人掌（可能有重边）。

　　对于所有的 $L(1\leq L\leq n-1)$ ，求出有多少不同的从节点 1 出发的包含 L 条边的简单路径。简单路径是指不重复经过任意一点。

　　$n\leq 10^5$

题解

　　首先我们把走一条边看作多项式 $x^1$ ，那么一条长度为 L 的路径就是其路径上的多项式的乘积。

　　接下来称“环根”为距离节点 1 最近的那个节点。

　　假设 $p_v$ 为点 v 对最终答案的贡献，那么 $p_v$ 是什么？分两种情况讨论：

　　　　1. v 属于某个环且 v 不是该环的环根。那么显然这个环的环根（设为 u）更靠近 1 ，假设 v 到 u 的两条路径长度分别是 a 和 b ，那么 $p_v=p_u \times (x^a+x^b)$ 。

　　　　2. 假设有一个点 u 不和 v 在同一个环中，且 u 距离 1 比 v 距离 1 更近，那么 $p_v=p_u\times x$ 。

 

　　于是到此为止我们已经可以轻松的解决 50 分了。

 

　　然而跳蚤国的疆域着实太大……

　　考虑对于仙人掌进行点分治，然后对于当前连通块 $T$ ，我们找点分中心 $x$ 。

　　怎么找点分中心？——类比找树的点分中心，"找一个结点，把和它相连的边都断了并且他在的每一个环上的边都要去掉（不去掉环上的其它结点）。这样找出连通块最大的最小作为重心。"

 

　　定义连通块的根为当前连通块中在原图距离 1 最近的点。

　　于是我们可以分治 FFT 求出点分中心 x 到 当前连通块的根 的多项式。

　　结合点分治，总复杂度为 $O(n\log^3 n)$ ，可能可以通过此题。

 

——VFleaKing

 

　　对于当前点分中心 x ，如果我们先将比 x 靠近连通块根的那个子仙人掌处理了，那么，我们会发现我们在这时要算的多项式大部分已经算好了。这里只需要做的就是合并。可以发现，从 x 追根溯源得到的这些多项式有 $O(\log n)$ 个，而且他们的最高次项指数是和对应的连通块的 size 相关的，又由于对于这些连通块，我们做的是点分治，所以这些多项式的最高次项指数是大约 2 倍两倍增长的。所以现在求点分中心 x 到 当前连通块的根 的多项式，只需要 $T(n) = T(n/2) + O(n\log  n) = O(n\log n)$ 的时间复杂度。

　　结合点分治，我们可以得到一个 $O(n\log ^2 n)$ 的优秀做法。

　　当然，底层实现的时候还是有一些细节需要注意，这里就不展开赘述了(饶了我吧，懒得写了……)。

　　由于博主人傻常数大，所以用时差点吃鸡了。

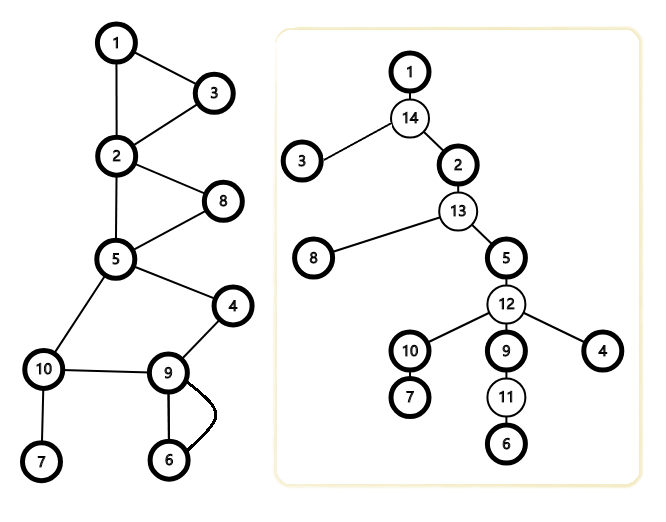
　　顺便赠送样例 2 的图，以及其圆方树。

 

 

代码

#include <bits/stdc++.h>
int Debug=0;
using namespace std;
typedef long long LL;
LL read(){
	LL x=0;
	char ch=getchar();
	while (!isdigit(ch))
		ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
const int N=(1<<18)+9,mod=998244353;
int Log[N];
int Pow(int x,int y){
	int ans=1;
	for (;y;y>>=1,x=(LL)x*x%mod)
		if (y&1)
			ans=(LL)ans*x%mod;
	return ans;
}
void Add(int &x,int y){
	if ((x+=y)>=mod)
		x-=mod;
}
int del(int x,int y){
	return x-y<0?x-y+mod:x-y;
}
int rev[N],w[N],A[N],B[N];
void FFT(int a[],int n){
	for (int i=0;i<n;i++)
		if (rev[i]<i)
			swap(a[i],a[rev[i]]);
	for (int t=n>>1,d=1;d<n;d<<=1,t>>=1)
		for (int i=0;i<n;i+=(d<<1))
			for (int j=0;j<d;j++){
				int tmp=(LL)w[j*t]*a[i+j+d]%mod;
				a[i+j+d]=del(a[i+j],tmp);
				Add(a[i+j],tmp);
			}
}
vector <int> Mul(vector <int> a,vector <int> b){
	static vector <int> ans;
	int n=1,d=0;
	for (;n<a.size()+b.size();n<<=1,d++);
	w[0]=1,w[1]=Pow(3,(mod-1)/n);
	for (int i=2;i<n;i++)
		w[i]=(LL)w[i-1]*w[1]%mod;
	for (int i=0;i<n;i++)
		rev[i]=(rev[i>>1]>>1)|((i&1)<<(d-1));
	for (int i=0;i<n;i++)
		A[i]=B[i]=0;
	for (int i=0;i<a.size();i++)
		A[i]=a[i];
	for (int i=0;i<b.size();i++)
		B[i]=b[i];
	FFT(A,n),FFT(B,n);
	for (int i=0;i<n;i++)
		A[i]=(LL)A[i]*B[i]%mod;
	w[1]=Pow(w[1],mod-2);
	for (int i=2;i<n;i++)
		w[i]=(LL)w[i-1]*w[1]%mod;
	FFT(A,n);
	int inv=Pow(n,mod-2);
	for (int i=0;i<n;i++)
		A[i]=(LL)A[i]*inv%mod;
	while (n>0&&!A[n-1])
		n--;
	ans.clear();
	for (int i=0;i<n;i++)
		ans.push_back(A[i]);
	return ans;
}
struct poly{
	vector <int> v;
	poly(){}
	poly(int x){
		v.clear();
		while (x>=(int)v.size())
			v.push_back(0);
		v[x]++;
	}
	void add_move(poly &p,int x){
		int s=max(v.size(),p.v.size()+x);
		while (v.size()<s)
			v.push_back(0);
		for (int i=0;i<p.v.size();i++)
			Add(v[i+x],p.v[i]);
	}
	poly operator << (int x){
		poly res=*this;
		reverse(res.v.begin(),res.v.end());
		while (x--)
			res.v.push_back(0);
		reverse(res.v.begin(),res.v.end());
		return res;
	}
	void operator += (poly A){
		while (v.size()<A.v.size())
			v.push_back(0);
		for (int i=0;i<A.v.size();i++)
			Add(v[i],A.v[i]);
	}
	void operator *= (poly A){
		v=Mul(v,A.v);
	}
}C;
poly operator + (poly A,poly B){
	C.v.clear();
	for (int i=max(A.v.size(),B.v.size());i>0;i--)
		C.v.push_back(0);
	for (int i=0;i<A.v.size();i++)
		Add(C.v[i],A.v[i]);
	for (int i=0;i<B.v.size();i++)
		Add(C.v[i],B.v[i]);
	return C;
}
poly operator * (poly A,poly B){
	C.v=Mul(A.v,B.v);
	return C;
}
struct Gragh{
	static const int M=N*4;
	int cnt,y[M],nxt[M],fst[N];
	void clear(){
		cnt=1;
		memset(fst,0,sizeof fst);
	}
	void add(int a,int b){
		y[++cnt]=b,nxt[cnt]=fst[a],fst[a]=cnt;
	}
}g;
int n,m,k;
int fa[N];
int dfn[N],low[N],st[N],Time=0,st_top=0,vise[N*2];
vector <int> circle[N],T[N];
void T_add(int a,int b){
	T[a].push_back(b);
	T[b].push_back(a);
}
void Tarjan(int x){
	dfn[x]=low[x]=++Time,st[++st_top]=x;
	for (int i=g.fst[x];i;i=g.nxt[i]){
		if (vise[i>>1])
			continue;
		vise[i>>1]=1;
		int y=g.y[i];
		if (!dfn[y]){
			Tarjan(y);
			low[x]=min(low[x],low[y]);
			if (low[y]>dfn[x]){
				T_add(x,y);
				fa[y]=x;
				st_top--;
			}
			else if (low[y]==dfn[x]){
				k++;
				T_add(x,k);
				circle[k].clear();
				circle[k].push_back(x);
				while (st[st_top]!=x&&low[st[st_top]]==dfn[x]){
					T_add(k,st[st_top]);
					circle[k].push_back(st[st_top]);
					fa[st[st_top]]=x;
					st_top--;
				}
			}
		}
		else
			low[x]=min(low[x],dfn[y]);
	}
}
int fad1[N],fad2[N];
int size[N],fimax[N],semax[N],vis[N],top[N];
int Tfa[N],Tdepth[N];
void dfsT(int x,int pre,int d){
	Tfa[x]=pre,Tdepth[x]=d;
	for (auto y : T[x])
		if (y!=pre)
			dfsT(y,x,d+1);
}
int Size,RT;
void get_size(int x,int pre){
	size[x]=x<=n?1:0,fimax[x]=semax[x]=0;
	for (auto y : T[x])
		if (y!=pre&&!vis[y]){
			get_size(y,x);
			size[x]+=size[y];
			if (size[y]>fimax[x])
				semax[x]=fimax[x],fimax[x]=size[y];
			else if (size[y]>semax[x])
				semax[x]=size[y];
		}
}
void get_root(int x,int pre){
	if (x<=n){
		fimax[x]=semax[x]=0;
		int f=Tfa[x];
		if (!vis[f]){
			if (f<=n)
				fimax[x]=Size-size[x];
			else
				fimax[x]=size[x]==fimax[f]?semax[f]:fimax[f];
		}
	}
	else {
		if (Size-size[x]>fimax[x])
			semax[x]=fimax[x],fimax[x]=Size-size[x];
		else if (Size-size[x]>semax[x])
			semax[x]=Size-size[x];
	}
	for (auto y : T[x])
		if (y!=pre&&!vis[y]){
			if (x<=n)
				fimax[x]=max(fimax[x],y<=n?size[y]:fimax[y]);
			get_root(y,x);
		}
	if (x<=n)
		if (!RT||fimax[RT]>fimax[x])
			RT=x;
}
poly up[N],dn[N],po,potmp;
int d_solve=0;
void solve(int x){
	get_size(x,0);
	Size=size[x],RT=0;
	get_root(x,0);
	assert(RT!=0);
	vis[x=RT]=++Time;
	top[x]=x;
	while (!vis[fa[top[x]]])
		top[x]=fa[top[x]];
	dn[x].v.push_back(0);
	Add(dn[x].v[0],1);
	for (auto y : T[x])
		if (!vis[y])
			if (y<=n){
				solve(y);
				if (Tdepth[y]>Tdepth[x])
					dn[x].add_move(dn[y],1);
			}
			else {
				vis[y]=vis[x];
				for (auto z : T[y])
					if (!vis[z]&&z!=x){
						solve(z);
						if (Tdepth[z]>Tdepth[y]){
							dn[y].add_move(dn[z],fad1[z]);
							dn[y].add_move(dn[z],fad2[z]);
						}
					}
				if (Tdepth[y]>Tdepth[x])
					dn[x].add_move(dn[y],0);
			}
	up[x].v.clear();
	if (vis[fa[x]]>vis[x]){
		int f=fa[x];
		po.v.clear();
		po=poly(0);
		while (f!=top[x]){
			if (top[f]==f){
				if (Tfa[f]>n){
					potmp.v.clear();
					potmp=po;
					po.v.clear();
					po.add_move(potmp,fad1[f]);
					po.add_move(potmp,fad2[f]);
				}
				else
					po=po<<1;
				f=fa[f];
			}
			else {
				po*=up[f];
				f=top[f];
			}
		}
		if (Tfa[x]>n){
			top[fa[x]]=top[x];
			up[fa[x]]=po;
			up[x].add_move(po,fad1[x]);
			up[x].add_move(po,fad2[x]);
		}
		else
			up[x].add_move(po,1);
	}
	else
		up[x].v.push_back(1);
	if (top[x]!=x)
		dn[top[x]]+=dn[x]*up[x];
	if (vis[Tfa[x]]>=vis[x]&&Tfa[x]>n)
		dn[top[x]]+=dn[Tfa[x]]*up[fa[x]];
}
int main(){
	Log[1]=0;
	for (int i=2;i<N;i++)
		Log[i]=Log[i>>1]+1;
	n=k=read(),m=read();
	g.clear();
	for (int i=1;i<=m;i++){
		int a=read(),b=read();
		g.add(a,b);
		g.add(b,a);
	}
	Tarjan(1);
	for (int i=n+1;i<=k;i++){
		int tmp=circle[i].size();
		for (int j=1;j<tmp;j++){
			fad1[circle[i][j]]=j;
			fad2[circle[i][j]]=tmp-j;
		}
	}
	dfsT(1,0,0);
	vis[0]=1;
	for (int i=1;i<=k;i++)
		dn[i].v.clear();
	Time=0;
	solve(1);
	while (dn[1].v.size()<n)
		dn[1].v.push_back(0);
	for (int i=1;i<n;i++)
		printf("%d\n",dn[1].v[i]);
	return 0;
}