UOJ#172. 【WC2016】论战捆竹竿 字符串 KMP 动态规划 单调队列 背包
原文链接https://www.cnblogs.com/zhouzhendong/p/UOJ172.html
题解
首先,这个问题显然是个背包问题。
然后,可以证明:一个字符串的 border 长度可以划分成 $O(log |S|)$ 个等差数列。
(以下图片摘自 金策 - 《字符串算法选讲》)

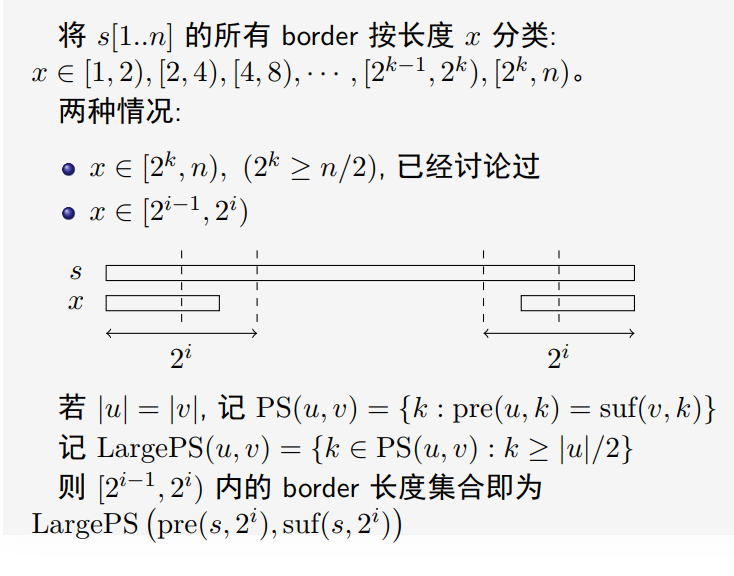

由于长度 n 可以随便取,所以我们可以在对n取模的意义下做背包,设 dis[i] 为 占用背包容量%n = i 时至少要占用多少背包容量,那么直接建 $n^2$ 条边跑一下 dijkstra 就可以在 $O(n^2\log n )$ 的时间复杂度内解决此题。
对于所有的长度,我们将其分组,保证每一组是一个等差数列。
我们枚举等差数列,依次将其加入背包。
假设最终背包中最多包含当前等差数列的一个元素,那么比较好做,直接单调队列就好了。
但是可以有多个当前等差数列的元素计入最终背包容量。也就是说,假设当前等差数列用 $v + kd$ 表示,那么可能会有 $tv + \sum k_i d$ 这种情况。这在对 n 取模的意义下非常难做。
于是我们考虑把它转化成对 $v$ 取模的意义下的结果,这样就方便多了。
考虑如何转化:先把原先在对 n 取模意义下的结果放到对 v 取模意义下的数组里,然后考虑每一个 $dis'[i]$ 都可以更新 $dis'[(i+n)\mod v ]$,即 $dis'[(i+n)\mod v] =min(dis'[(i+n)\mod v],dis'[i] + n)$ 。
把转移形成的环搞出来,dp转移一下就可以得到新的dis数组。
剩下的单调队列+dp也类似。
于是时间复杂度是 $O(n\log n)$ 。
代码
#pragma GCC optimize("Ofast","inline")
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define fi first
#define se second
using namespace std;
typedef long long LL;
LL read(){
LL x=0,f=0;
char ch=getchar();
while (!isdigit(ch))
f|=ch=='-',ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return f?-x:x;
}
const int N=500005;
const LL INF=2e18;
int T,n,m;
LL w;
int Fail[N],nf[N];
struct brd{
int v,d,c;
}b[N];
char s[N];
LL dis[N],rng;
LL gcd(LL a,LL b){
return b?gcd(b,a%b):a;
}
void Trans(LL nr){
static LL d[N];
for (int i=0;i<nr;i++)
d[i]=INF;
for (int i=0;i<rng;i++)
d[dis[i]%nr]=min(d[dis[i]%nr],dis[i]);
int g=gcd(rng,nr);
for (int t=0;t<g;t++){
int e=nr/g*2,_i=t,rg=rng%nr;
for (LL i=t,j=0;j<e;i+=rng,j++){
d[_i]=min(d[_i],d[_i<rg?_i-rg+nr:_i-rg]+rng);
if ((_i+=rg)>=nr)
_i-=nr;
}
}
rng=nr;
for (int i=0;i<rng;i++)
dis[i]=d[i];
}
pair <LL,LL> Q[N*2];
int head,tail;
void DP(int d,int c){
int g=gcd(rng,d);
for (int t=0;t<g;t++){
head=1,tail=0;
int e=rng/g*2,_i=t;
for (LL i=t,j=0;j<e;i+=d,j++){
if (head<=tail&&Q[head].fi+(LL)c*d<=i)
head++;
if (head<=tail)
dis[_i]=min(dis[_i],Q[head].se+rng+i);
while (head<=tail&&Q[tail].se>=dis[_i]-i)
tail--;
Q[++tail]=make_pair(i,dis[_i]-i);
if ((_i+=d)>=rng)
_i-=rng;
}
}
}
int main(){
T=read();
while (T--){
n=read(),w=read();
scanf("%s",s+1);
Fail[1]=0;
for (int i=2;i<=n;i++){
int k=Fail[i-1];
while (k>0&&s[k+1]!=s[i])
k=Fail[k];
if (s[k+1]==s[i])
k++;
Fail[i]=k;
}
m=0;
for (int i=n;i>0;i=Fail[i])
nf[Fail[i]]=i;
for (int j=0;j<n;j=nf[j]){
int i=n-j;
if (j==0)
m++,b[m].v=i,b[m].d=0,b[m].c=1;
else if (!b[m].d)
b[m].d=b[m].v-i,b[m].c++,b[m].v=i;
else if (b[m].v-b[m].d==i)
b[m].v=i,b[m].c++;
else
m++,b[m].v=i,b[m].d=0,b[m].c=1;
}
if (!b[m].d)
b[m].d=1;
clr(dis);
rng=n;
for (int i=0;i<n;i++)
dis[i]=INF;
dis[0]=n;
for (int i=1;i<=m;i++){
Trans(b[i].v);
DP(b[i].d,b[i].c);
}
LL ans=0;
for (int i=0;i<rng;i++)
if (dis[i]<=w)
ans+=w/rng-dis[i]/rng+(w%rng>=dis[i]%rng?1:0);
cout<<ans<<endl;
}
return 0;
}


