UOJ#109. 【APIO2013】TASKSAUTHOR 构造
原文链接www.cnblogs.com/zhouzhendong/p/UOJ109.html
题解
Task1:
造一个101个点,没有边的图。
Task2:
令 \(n = 100\)。造一条从 \(n\) 到 \(1\) 的链,然后不断随便加边权为 \(\infty\) 的边,尽量多加。
最后问 \(10\) 次 \(n\) 到 \(1\) 的最短路即可。
算一下刚好卡掉了bellman-ford
Task3:
做法和 Task1 一样。造一个101个点,没有边的图。
Task4:
首先,由于 \(n\leq \frac T 2 = \frac {157} 2\),无论如何也卡不掉 Floyd,所以只要考虑卡 dijkstra。
注意到他这个魔改版的 dijkstra 其实和 spfa 的某个优化版本很像。
我们考虑造一个图把它卡成指数级的。
首先我们考虑一下这么一个结构:
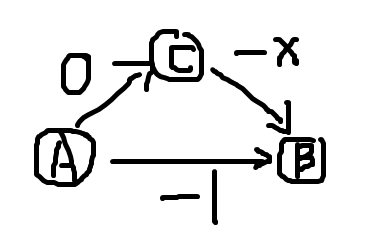
其中 \(2 \leq x\)。我们发现会先松弛 B,再松弛 C,再松弛 B。于是我们想办法把这个元件连成一排,并使得每次某一个点被松弛时,都要把从它到最右端点的每一条路径松弛一遍。
所以图大概长这样:
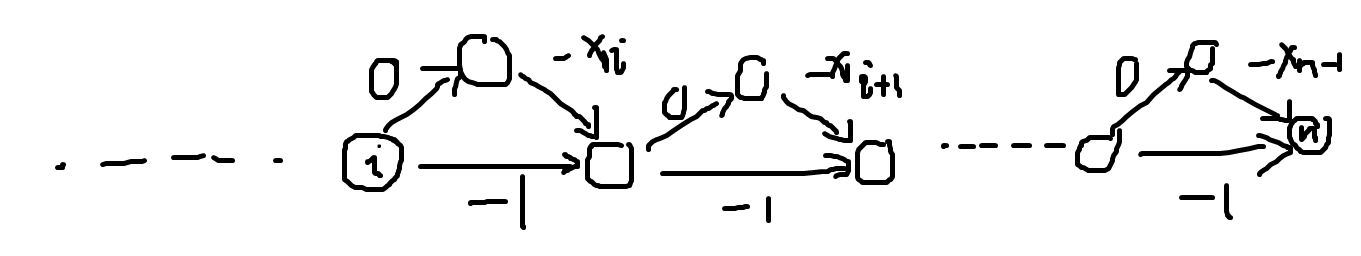
假设当前节点 \(i\) 被松弛了,容易发现它到 \(n\) 的所有路径中最难松弛的是沿着 \(-1\) 走的那条,所以有:
令 \(x _ i = 2 ^ {n-i}\) 即可。
Task5:
和 Task2 做法类似。
Task6:
和 Task4 做法类似。
Task7:
其实由题目里给出的条件可以确定 \(E = 1501\)。
我们发现它的算法就是一个裸的 dfs,于是随便造一个图就卡掉了。
Task8:
首先 \(E = 1501\)。我的想法是让这个 dfs 在第一次递归到底的时候就得到一个解。这意味着该图可以二染色,是一个二分图。于是我们只需要让 \(1\cdots \lfloor n/2 \rfloor\) 为左侧点,剩余的为右侧点,然后为了保证每个点第一次被枚举的颜色就是对的,我们让左侧的一个点连向右侧的所有点,然后剩下的边随便连即可。


