数论函数 - 莫比乌斯函数与莫比乌斯反演 - 基础杜教筛
原文链接http://www.cnblogs.com/zhouzhendong/p/8627380.html
省选后发现我数学好差。于是先从数论开始学习。
如果发现本文有任何错误,欢迎留言指正。
本文内容大致如下:
- 数论函数基础知识
- 狄利克雷卷积与莫比乌斯反演
- 杜教筛
- 例题
数论函数基础知识
几个定义
- 数论函数:定义域为正整数的函数。(默认下面提到的函数全部都是数论函数)
- 积性函数:如果$a,b$满足$gcd(a,b)=1$,则$f(ab)=f(a)f(b)$。
- 完全积性函数:对于任何$a,b$,满足$f(ab)=f(a)f(b)$。
几个积性函数
$1.$欧拉函数:$\varphi(n)=\large\sum_{i=1}^{n}[gcd(i,n)=1]$,是积性函数。
$2.$莫比乌斯函数:$\large\mu$ 当$n$有平方因子的时候,$\mu(n)=0$,否则设$n$为$k$个不同质因子的积,则$\mu(n)=(-1)^{k}$。
$3.$除数函数:这不是完全积性函数。$\sigma_{a}n=\sum_{d|n}d^{a}$。其中$d(n)=\sigma_{0}(n)$为$n$的因数个数,$\sigma_{1}(n)=\sigma(n)$为$n$的所有因数之和。
$4.$幂函数:这是完全积性函数。$id_k(n)$,表示$n^k$。
$5.$单位函数:这是完全积性函数。$e(n)=[n=1]$。
Dirichlet卷积
定义
函数$f$与$g$的Dirichlet卷积定义如下:
$$(f*g)(n)=\sum_{d|n}f(d)\times g(\frac{n}{d})$$
个人认为看起来比较舒服的写法:
$$(f*g)(n)=\sum_{ij=n}f(i)\times g(j)$$
于是,就很容易发现:
$$(f*g*h)(n)=\sum_{ijk=n}f(i)\times g(j)\times h(k)$$
几点性质
交换律:略
结合律:略
分配律:$f*(g+h)=f*g+f*h$
单位元:$f*e=f$
如果$f,g$都为积性函数,那么$f*g$也为积性函数。
对于任何一个函数$f$,则一定存在一个函数$g$满足$f*g=e$,则$g$叫做$f$的Dirichlet逆。
计算Dirichlet卷积。
设$h=f*g$
计算$h(n)$:
显然直接根据定义,枚举因数即可。时间复杂度$O(\sqrt n)$。
h(n)=0; for (int i=1;i*i<=n;i++){ if (n%i) continue; h(n)+=f(i)*g(n/i); if (i*i!=n) h(n)+=f(n/i)*g(i); }
计算$h$,其中$h$的定义域为正整数$1$~$n$。
显然$O(\sqrt n)$太慢了。于是:
经典简单套路。先枚举一个数i,然后再枚举倍数。时间复杂度$O(n\ log\ n)$。
memset(h,0,sizeof h); for (int i=1;i<=n;i++) for (int j=1;i*j<=n;j++) h(i*j)+=f(i)*g(j);
几个Dirichlet卷积
除数函数卷上1。($1=id_0$)
$$d(n)=\sum_{d|n}1\Rightarrow d=1*1$$
$$\sigma(n)=\sum_{d|n}d\Rightarrow \sigma=id*1$$
莫比乌斯函数与1的卷积。
(我一开始制杖了,好久没看懂。)
其中$k$为$n$的不同种类的质因数个数。
$$\sum_{d|n}\mu(d)=\sum_{i=0}^{k}(-1)^i\times \binom{k}{i}=(1-1)^{k}=0^{k}$$
其中,对于$0^0$没有定义。但是考虑到满足$k=0$的只有$n=1$,而$\mu(1)=1$,所以:
$$\sum_{d|n}\mu(n)=[n=1]=e(n)$$
于是就有:
$$e=\mu*1$$
这个对于之后的莫比乌斯反演十分重要,请务必记住。
另一个常用的卷积:
$$\varphi*1=??$$
考虑到,若$d$为$n$的因数,则$\varphi(d)$即与$n$的最大公约数为$\frac{n}{d}$的数的个数。所以:
$$\sum_{d|n}\varphi(d)=n$$
$$\Longrightarrow \varphi*1=id$$
关于幂函数:
$$id_k\times(a*b)=(id_k\times a)*(id_k\times b)$$
$$(\varphi\times id_k)*id_k=id_{k+1}$$
莫比乌斯反演
莫比乌斯函数的一个重要性质
考虑前文提到的
$$e=\mu*1$$
这个式子也说明了$\mu$和$1$在Dirichlet卷积的意义下互为逆元。
于是我们就可以通过这个来反演了。
因数反演
已知$g=f*1$,让你用$g$函数的式子来表示$f$。
$$g(n)=\sum_{d|n}f(d)$$
考虑到两边同时在Dirichlet卷积的意义下除以$1$。而$\mu$和$1$在Dirichlet卷积意义下互为逆元,所以除$1$可以卷上$\mu$代替。
$$g=f*1\Longrightarrow f=g*\mu$$
不服??看下面的推导。
$$f*1=g\Longrightarrow f*1*\mu=g*\mu\Longrightarrow f*e=g*\mu\Longrightarrow f=g*\mu$$
倍数反演
这个嘛,大概得注重一下函数的具体定义域。
$$g(n)=\sum_{n|d}f(d)\Longrightarrow f(n)=\sum_{n|d}\mu(\frac{d}{n})g(d)$$
套路套路!!
一句话的套路
1. 枚举gcd的取值。
2. 交换倍数和约数。
3. 用莫比乌斯函数求和替换$[a=1]$这种表达式。
4. 改写求和指标。
5. 整除分块。
一些较为具体的套路(反正都是套路,数学推导能力极强的dalao可以不记……)
一、计算函数$f$与$1$的Dirichlet卷积的某一项。即$g=f*1$,求$g(n)(n\leq 10^{18})$。
1. 我们对$n$进行质因数分解,使用Pollard_rho算法,复杂度$O(n^{\frac{1}{4}}\log n)$。
2. 设$n=\prod_{i=1}^{t}p_i^{k_i}$,$g(n)=\sum_{d|n}f(d)$,请您自行推导下面的公式(时间复杂度$O(log\ n)$):
$$g(n)=\prod_{i=1}^{t}\sum_{j=0}^{k_i}f(p_i^j)$$
二、整除分块。求$f(n)=\sum_{i=1}^{n}g(i)\times\left\lfloor\frac{n}{i}\right\rfloor$。
1. 考虑到$\left\lfloor\frac{n}{i}\right\rfloor$只有$O(\sqrt n)$种取值。对于相同的$\left\lfloor\frac{n}{i}\right\rfloor$,$i$的取值范围为:
$$\Large \left[\left\lfloor\frac{n}{\left\lfloor\frac{n}{i}\right\rfloor+1}\right\rfloor+1,\left\lfloor\frac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor\right]$$
2. 通过预处理函数$g$的前缀和,做到$O(1)$算函数$g$的区间和,整个求$f$就可以在$O(\sqrt n)$解决。
3. 同时有$n,m$也类似,读者可以自行推导。
三、
$$\varphi(n)=\sum_{d|n}\mu(d)\times\frac{n}{d}\Longrightarrow\varphi=\mu*id$$
推导??
先回忆一下之前提到的两个Dirichlet卷积。
$$e=\mu*1$$
$$id=\varphi*1$$
于是
$$\varphi*1=id\\ \Longrightarrow \varphi*1*\mu=id*\mu\\ \Longrightarrow\varphi*e=id*\mu\\ \Longrightarrow\varphi=\mu*id$$

啊,我是不是又推了一遍莫比乌斯反演??
对莫比乌斯反演还是不熟悉的同学们注意了,上面的那个是$\varphi$的莫比乌斯反演,注意一下。
四、注意注意!!莫比乌斯反演经典套路!!
现在有个积性函数$f(n)$,设$n<m$,则:
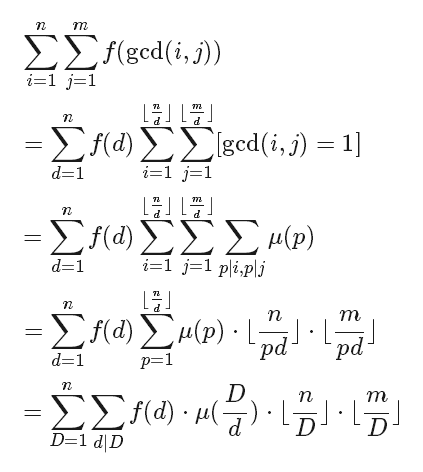
于是原来的式子就变成了求$f*\mu$了,再用上整数分块就可以快速搞定了。
UPD(2019-02-24): 突然想起来补了这段话。
至少在我写这个课件的时候及以前,我的想法是:

直到我看见了这个……

(图片来自 《炫酷的反演魔术》—— VFleaKing)
杜教筛
问题模型
给定一个函数$f(n)$(例如$\varphi,\mu$),然后让你求$S(n)=\sum_{i=1}^{n}f(i)$的值(有模数)$n\leq 10^{10}$。
构造
直接求出$S(n)$会十分困难,所以我们考虑构造一个函数$g$,使得$f*g$的前缀和非常好求。
$$\sum_{i=1}^{n}\sum_{j|i}f(i)g(\frac{i}{j})=\sum_{ij\leq n}f(i)g(j)=\sum_{i=1}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)$$
$$g(1)S(n)=\sum_{ij\leq n}f(i)g(j)-\sum_{i=2}^{n}g(i)S\left(\left\lfloor\frac{n}{i}\right\rfloor\right)$$
一些补充
于是我们就可以直接记忆化dfs搞定了。
但是复杂度可以更好。
我们考虑先预处理$k$个前缀和。时间复杂度$O(k+\frac{n}{\sqrt k})$。
于是取$k=n^{\frac{2}{3}}$,复杂度为$O(n^{\frac{2}{3}})$。
考虑到
$$\left\lfloor\frac{n}{ab}\right\rfloor=\left\lfloor\frac{\left\lfloor\frac{n}{a}\right\rfloor}{b}\right\rfloor$$
所以,由于$\frac{n}{n^{\frac{2}{3}}}=n^{\frac{1}{3}}$,所以会被算到的$S(i)$只有$O(n^{\frac{1}{3}})$个。
这边还有一个重要套路。
存$S(i)$不是要hash吗??直接把$S(i)$放到$f(n/i)$里面就可以了。
你可以考虑一下$f=\varphi$或者$f=\mu$的情况。此时可以取$g=1$。
当然$f$可能会是更加复杂的函数,于是你就要对应的找比较好的$g$了。
一些例题
仅用积性函数性质进行推导:
BZOJ3560 DZY loves math V
莫比乌斯函数与莫比乌斯反演(套路)
BZOJ3561 DZY loves math VI
51Nod1675 序列变换
BZOJ4816 [Sdoi2017]数字表格


