2018牛客网暑假ACM多校训练赛(第四场)D Another Distinct Values 构造
原文链接https://www.cnblogs.com/zhouzhendong/p/NowCoder-2018-Summer-Round4-D.html
题目传送门 - https://www.nowcoder.com/acm/contest/142/D
题意
多组数据 $T\leq 200$
每组数据给定一个 $n$ ,让你构造一个只包含 $-1,1,0$ 的矩阵,使得 每行的和,每列的和 ,共 $2n$ 个数,都互不相同。
如果没有方案,输出 impossible ;否则输出 possible ,并输出方案。
$n\leq 200$
题解
首先放一下官方题解证明 $n$ 为奇数时无解。
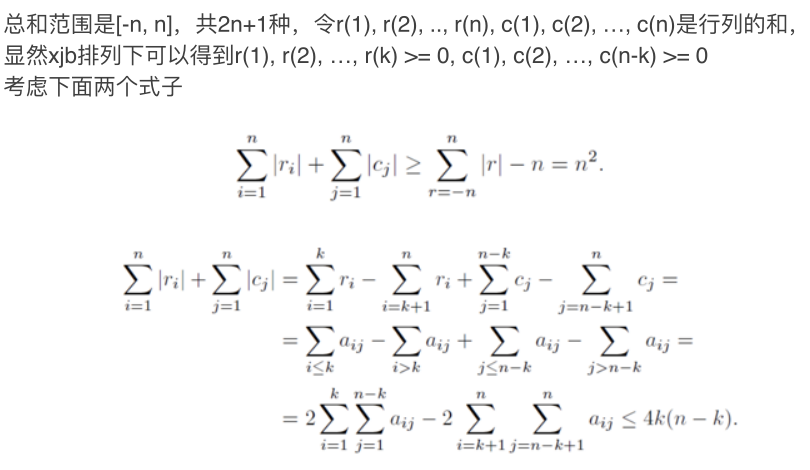
然后讲一讲我自己的构造方案。
令 $A,B,C,D$ 为长宽为 $\cfrac n2$ 的矩阵。令
$$A=\left [\begin{matrix}1&0&0&\cdots&0&0&0\\1&1&0&\cdots&0&0&0\\1&1&1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\1&1&1&\cdots&1&0&0\\1&1&1&\cdots&1&1&0\\1&1&1&\cdots&1&1&1\\\end{matrix}\right ]$$
$$B=\left [\begin{matrix}1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\\end{matrix}\right ]$$
$$C=-\left [\begin{matrix}1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\1&1&1&\cdots&1&1&1\\\end{matrix}\right ]$$
$$D=-\left [\begin{matrix}0&1&1&\cdots&1&1&1\\0&0&1&\cdots&1&1&1\\0&0&0&\cdots&1&1&1\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&\cdots&0&1&1\\0&0&0&\cdots&0&0&1\\0&0&0&\cdots&0&0&0\\\end{matrix}\right ]$$
令
$$M=\left (\begin{matrix}A&C\\B&D\\\end{matrix}\right )$$
矩阵 $M$ 即为答案。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=205;
int T,n;
int a[N][N];
int main(){
scanf("%d",&T);
while (T--){
scanf("%d",&n);
if (n&1){
puts("impossible");
continue;
}
puts("possible");
memset(a,0,sizeof a);
for (int i=1;i<=n/2;i++)
for (int j=1;j<=n/2;j++)
a[i+n/2][j]=1,a[i][j+n/2]=-1;
for (int i=1;i<=n/2;i++)
for (int j=1;j<=i;j++)
a[i][j]=1;
for (int i=1;i<n/2;i++)
for (int j=1;j<=i;j++)
a[n-i][n-j+1]=-1;
for (int i=1;i<=n;i++,puts(""))
for (int j=1;j<=n;j++)
printf("%d ",a[i][j]);
}
return 0;
}


