LCT入门教程
原文链接 https://www.cnblogs.com/zhouzhendong/p/LCT.html
由于我感觉之前的ppt版过于愚蠢而且之前使用的编辑器不是 Markdown,所以我把它变成了网页版。
LCT 入门总结
问题模型
给定一棵森林,每一个点有一个权值。请你支持以下操作:
- 单点修改权值。
- 询问一条链点权和。
- 删除一条边。
- 修改一条边。
设点数和操作数都为 \(n\),则要求做到 \(O(n\log n)\) 的时间复杂度。
什么是 LCT
LCT 全称 Link-Cut Tree ,用于处理一类动态树问题。
LCT 将所有的边分成实边和虚边两类,形成若干条实链,并对此建立一个辅助树。
对于每一条实链,以节点深度为关键字将节点用splay存起来。
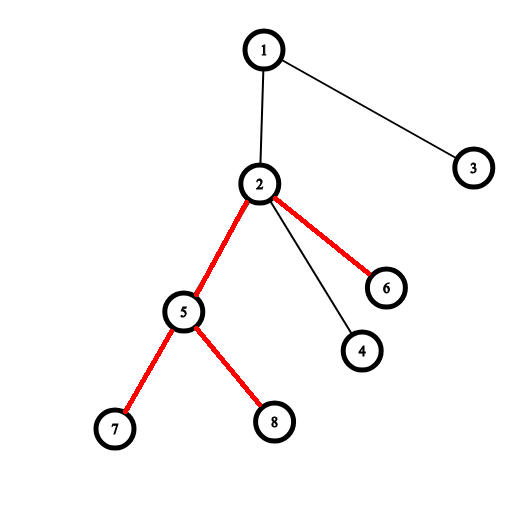
一个辅助树例子


其中红色的是实边,黑色的是虚边。
那么在原树中,2 的父亲是 8 ,7 的父亲是 1 。其中用灰色箭头连接起来的 1-7-5-8-2-6 是一条树链。
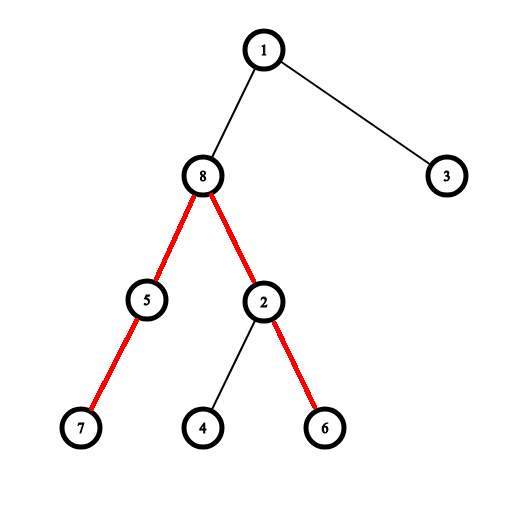
下图就是上图对应的原树。
如何维护 LCT
前置技巧 splay
略
Access
Access(x) 的作用是打通一条从节点x 到达连通块根的路径。
例如在下图中 Access(8)
令初始时 tmp = 0(注意此时 \(x = 8\))
第一步,把节点x splay 到它所在的实链对应的平衡树顶端。
然后把 tmp 接到 x 以下。等价于将实链中,深度大于 x 的部分切断。然后令 tmp = x, x = fa[x]; 此时 \(x = 1\),于是接下来对于节点1 做 splay,也切断深度大于 1 的一部分,再将 tmp 接上去。不断向根循环进行操作,最终得到下图(结合代码理解更佳):

性质
如上图所示, Access(8) 之后, 节点8 一定是这条实链的最深节点。如果将他 splay 到根,那么它一定没有右儿子。
代码
void access(int x){
int t=0;
while (x){
splay(x),son[x][1]=t;
t=x,x=fa[x];
}
}
换根(rever)
rever(x) 的作用是将 x 变成连通块的根。
代码
void rever(int x){
access(x),splay(x),rev[x]^=1;
}
简单解释
access(x):打通到根路径。splay(x):将 x 提到根(注意这时候 x 是没有右子树的)。由于这里是换根,如果这样就结束了,那么 x 的深度没有变。既然换根,那么也要换深度,所以打上翻转标记来实现深度翻转。
link
link(x,y) 即在 x 与 y 之间连边。
代码
void link(int x,int y){
rever(x),fa[x]=y;
}
简单解释
将 x 变成根之后, x 就没有 father 了,这样就取消了 x 的 father 的干扰;然后再建立 x->y 的虚边。
cut
代码
void cut(int x,int y){
rever(x),access(y),splay(y),fa[x]=son[y][0]=0;
}
简单解释
rever(x): 将 x 变成该连通块的根。
access(y): 打通从 y 到该连通块根 x 的一条路径。
splay(y): 将 y 已到辅助树根位置。
这时,由于 x 和 y 在同一连通块切有直接连边,又因为 x 的深度比 y 小,所以在辅助树中 x 必然是 y 的左子节点,直接断开就好了。
时间复杂度证明
https://www.cnblogs.com/zhouzhendong/p/JunTanFenXi.html
一个维护树链权值和的例子
int n,m;
int fa[N],son[N][2],rev[N],val[N],sum[N];
bool isroot(int x){
return son[fa[x]][0]!=x&&son[fa[x]][1]!=x;
}
void pushup(int x){
sum[x]=sum[son[x][0]]+sum[son[x][1]]+val[x];
}
void pushdown(int x){
if (rev[x])
rev[son[x][0]]^=1,rev[son[x][1]]^=1,swap(son[x][0],son[x][1]),rev[x]=0;
}
void pushadd(int x){
if (!isroot(x))
pushadd(fa[x]);
pushdown(x);
}
int wson(int x){
return son[fa[x]][1]==x;
}
void rotate(int x){
if (isroot(x))
return;
int y=fa[x],z=fa[y],L=wson(x),R=L^1;
if (!isroot(y))
son[z][wson(y)]=x;
fa[x]=z,fa[y]=x,fa[son[x][R]]=y;
son[y][L]=son[x][R],son[x][R]=y;
pushup(y),pushup(x);
}
void splay(int x){
pushadd(x);
for (int y=fa[x];!isroot(x);rotate(x),y=fa[x])
if (!isroot(y))
rotate(wson(x)==wson(y)?y:x);
}
void access(int x){
int t=0;
while (x){
splay(x);
son[x][1]=t;
pushup(x);
t=x;
x=fa[x];
}
}
void rever(int x){
access(x);
splay(x);
rev[x]^=1;
}
void link(int x,int y){
rever(x);
fa[x]=y;
}
void cut(int x,int y){
rever(x);
access(y);
splay(y);
fa[x]=son[y][0]=0;
}
例题
[HNOI2010] 弹飞绵羊
沿着一条直线有n个装置,每个装置设定初始弹力系数ki,当绵羊达到第i个装置时,它会往后弹ki步,达到第i+ki个装置,若不存在第i+ki个装置,则绵羊被弹飞。当它从第i个装置起步时,被弹几次后会被弹飞?此外,还会中途修改某个弹力装置的弹力系数,任何时候弹力系数均为正整数。
\(n\leq 10^5\)
提示
我们把弹簧装置看做 x 的效果看做一条从节点 i 到节点 i+ki 的边,那么必然会得到一棵树。
我们设一个总的根节点 root 表示弹飞之后到达的节点,那么显然节点 i 的答案就是 i 到 root 的距离。
代码
http://www.cnblogs.com/zhouzhendong/p/8028221.html
[SDOI2008] Cave
有 n 个点,一开始没有连边。有 m 次操作:
操作有 3 种类型:一种是连接某两个点,一种是断开某一条边。还有一种是询问两个点是否连通。
操作过程中保证整个图是森林。
\(n\leq 10^4,m\leq 2\times 10^5\)
提示
主要问题是判断两个点是否在同一个连通块里。注意到如果他们在同一个连通块,那么他们的根是相同的。
判断 x y 是否在同一个连通块的做法很多,随便说几种:
- rever(x); access(y); splay(y); 找到 y 对应的splay里优先级最高的点看看是不是 x 就好了。(就是不断往左节点跳)
- access(x); splay(x); 找到 x 对应的splay里优先级最高的点 k1; access(y); splay(y) 找到 y 对应的splay里优先级最高的点 k2 ,判断 k1 是否等于 k2 即可。
“找优先级最高的点”本质是找原树的根。
代码
http://www.cnblogs.com/zhouzhendong/p/8029252.html
BZOJ2843 极地旅行社
有n座岛,每座岛上的企鹅数量虽然会有所改变,但是始终在[0, 1000]之间。你的程序需要处理以下三种命令:
- "bridge A B"——在A与B之间建立一座大桥(A与B是不同的岛屿)。由于经费限制,这项命令被接受,当且仅当A与B不联通。若这项命令被接受,你的程序需要输出"yes",之后会建造这座大桥。否则,你的程序需要输"no"。
- "penguins A X"——根据可靠消息,岛屿A此时的帝企鹅数量变为X。这项命令只是用来提供信息的,你的程序不需要回应。
- "excursion A B"——一个旅行团希望从A出发到B。若A与B连通,你的程序需要输出这个旅行团一路上所能看到的帝企鹅数量(包括起点A与终点B),若不联通,你的程序需要输出"impossible"。
提示
直接多维护一个树链和就好了。
只需要在改变辅助树实链形态的时候pushup就好了。
代码
http://www.cnblogs.com/zhouzhendong/p/8033088.html
BZOJ2631
一棵n个节点的树,节点有权值,m次操作。
要支持: 删边、连边、区间求和、区间加、区间乘。
保证操作过程中不出现环。
\(n,m\leq 100000\)
提示
把你学过的线段树的pushup放到lct上就好了。
代码
http://www.cnblogs.com/zhouzhendong/p/8038368.html
BZOJ2594 [Wc2006] 水管局长数据加强版
n个点的图,m条带权边,有q次操作
操作有两个类型:
- 在节点x到y的之间所有路径中找一条路径,使得这条路径上的最大边权尽量小,输出这个最小值。
- 删除某一条边
操作过程中保证图连通。
\(n,q\leq 10^5,m\leq 10^6\)
提示
这题需要用到“时光倒流”。
首先,我们先假装边都删好了,然后倒过来一边加边,一边回答。
其次,我们要找的这条边,肯定在当前最小生成树中 x 到 y 路径上的。
于是我们需要维护边权 max 。但是到现在位置,我们所知 LCT 只能维护点权 max。
只需要把边看做一个点,这个点向这条边连接的两个点各连一条边即可。
代码
http://www.cnblogs.com/zhouzhendong/p/8041313.html
BZOJ3514 Codechef MARCH14 GERALD07加强版
N个点M条边的无向图,询问保留图中编号在[l,r]的边的时候图中的联通块个数。
\(N,M,Q\leq 200000\)
提示
- 首先,将边按照编号顺序依次加入图中。每当出现环时,将环中最早加入的边弹出。记第 i 条边被弹出的时间为 \(T_i\) ,表示在第 \(T_i\) 条边加入的时候,第 i 条边被弹出了。
- 询问一段区间的边出现的情况下的 连通块个数,可以转化成 点数 - 任意一个生成森林的边数。那么如何求边数?对于一对 \([L,R]\) ,满足 \(L\leq i\leq R, R < T_i\) 的点数。所以只要主席树维护一下就好了。
代码
由于写代码在很久以前,所以代码和这里的做法简述可能有些偏差,但无伤大雅。
http://www.cnblogs.com/zhouzhendong/p/8042515.html
UOJ#207. 共价大爷游长沙
给定一个 n 个节点的树,有 m 次操作,操作有以下 4 种类型:
- 给定四个正整数 x,y,u,v,表示先删除连接点x和点y的无向边,保证存在这样的无向边,然后加入一条连接点u和点v的无向边,保证操作后的图仍然是一棵树。
- 给定两个正整数 x,y,表示在 S 中加入点对 (x,y)。
- 给定一个正整数 x,表示删除第 x 个加入 S 中的点对,即在第 x 个操作2中加入 S 中的点对,保证这个点对存在且仍然在 S 中。
- 给定两个正整数 x,y,询问连接点 x 和点 y 的边是否属于 S 集合中的所有路径的交集,保证存在这样的无向边且此时 S 不为空。
\(n\leq 10^5,m\leq 3\times 10^5\)
提示
首先,我们发现询问一条边(x,y)是否是所有路径的交集,可以转化成:
将 x 变成根,询问在S集合中的每一条路径是否都有且仅有一个端点出现在 y 子树中。
于是,问题转化成了维护子树信息。对于每一条路径的两端点,我们 random 一个值,并 xor 给这两个端点,于是原问题就变成了 LCT 维护子树节点权值 xor 。
LCT 维护子树信息和维护树链信息有些差别。我们在 LCT 的时候,再对于每一个节点维护其虚儿子的信息。由于 LCT 涉及修改虚儿子的操作十分少,所以只需要在修改边的虚实关系的时候顺便维护一下就好了。
代码
https://www.cnblogs.com/zhouzhendong/p/UOJ207.html
更多习题
BZOJ3091 城市旅行
BZOJ2759 一个动态树好题
BZOJ4025 二分图(这题也有其他做法)
鸣谢
感谢 cly 大爷强行要学动态dp,蒟蒻zzd也去学了学,顺便学了全局平衡二叉树才发现我之前的LCT博客写错了。
感谢 emoarix 在很久以前提供的例题一道 BZOJ4025。
感谢 Yang Zhe《SPOJ375 QTREE 解法的一些研究》使我从中获益。


