Codeforces 980F Cactus to Tree 仙人掌 Tarjan 树形dp 单调队列

原文链接https://www.cnblogs.com/zhouzhendong/p/CF980F.html

题目传送门 - CF980F

题意

　　给定一个 $n$ 个节点 $m$ 条长为 $1$ 的边的每个点最多只属于一个环的仙人掌。

　　现在请你通过删边把仙人掌转化成树。

　　对于每一个点，输出在所有不同的删边方案中，  距离该点最远的点与他之间的距离值 的最小值。

　　$n\leq 5\times 10^5$

题解

　　首先，我们跑一跑 Tarjan ，找出每一个双联通分量。

　　然后我们把每一个双联通分量里面的点按照顺序存在 vector 里面。

　　我们称每一个环中连向环的父亲环的节点为该环的 环根 。

　　然后我们考虑从下网上跑一跑 树形DP ，处理出以每一个点为根的子仙人掌中所有不同的删边方式中最远点距离的最小值。

　　这次 DP 结束后，我们记第 $i$ 个节点的结果为 $Deep_i$ 。其中，对于任意环根 $i$，特殊地， $Deep_i$ 的涉及范围为以当前环为根的子仙人掌。

　　为了后面的方便，对于任意环根我们还需要记录两个值 ： $spDeep_i,\ \ usDeep_i$ 。

　　具体含义见下图：

　　

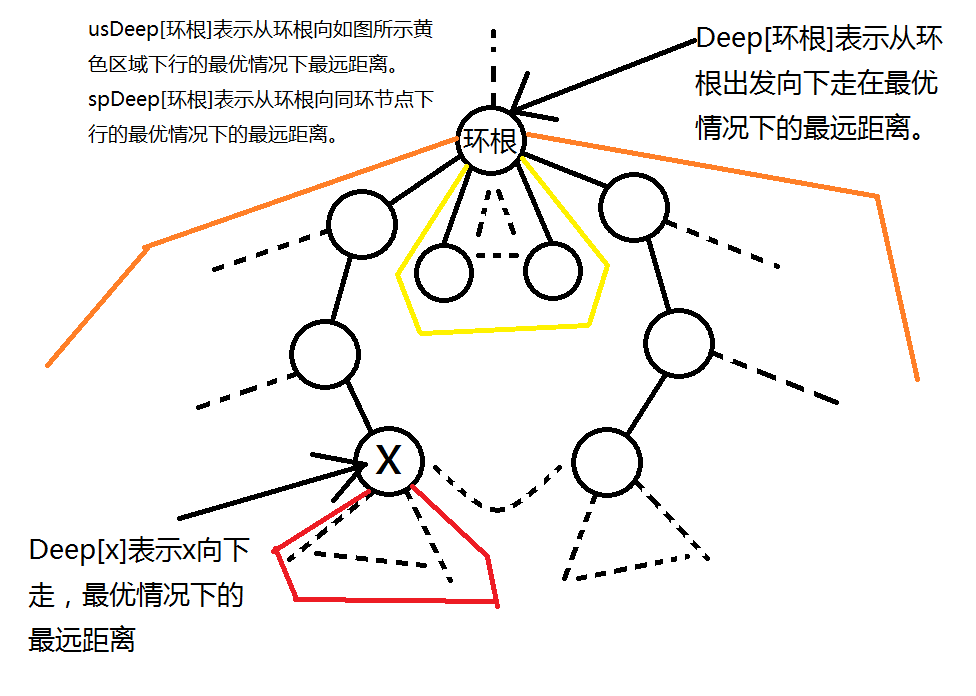
　　对于环根 $x$ ，显然有 $Deep_x=\max(spDeep_x,usDeep_x)$，要求 $spDeep_x$ 可以通过预处理前后缀 $\max$，然后枚举该环的断边来得到。

　　

　　下一步，我们需要处理一个 $Far_i$。

　　对于环根： $Far_i$ 表示下一步从该环根上行，最优情况下的最远距离。

　　对于普通的点： $Far_i$ 表示下一步从该点向同环的点走，最优情况下的最远距离。

 

　　只要处理出这个东西，则第 $i$ 个节点的答案就是 $\max(Far_i,Deep_i)$ 了。

　　我们考虑一下那些会对 $Far_i$ 有贡献的节点。

　　第一种，当前点不是环根，则向同环的节点走会有贡献。

　　第二种，当前点是环根，向同环的点和向父亲走都会有贡献。注意，这个向父亲走的贡献有两种，一种是由父亲的其他子节点来的，一种是由父亲的同环节点来的(父亲的 $Far$ )。

　　如果是环根，那么我们特殊处理即可。

　　现在考虑处理非环根的 $Far$ 。

　　通过证(感性)明(理解)，我们可以发现，对于当前环，当起始点在被顺时针遍历的时候，最优方案下删掉的边也是 大致 顺时针移动的。

　　我们可以维护当前点两个方向的节点最大贡献值尽量平衡来获取最优解。

　　于是我们可以用两个单调队列来实现。这一部分是关键。需要把环铺成三倍长度，并加上特定的权值。

　　这里具体不展开描述了，可以参见代码。

　　我由于弹出单调队列 QR 的时候少弹了一个位置， wa on test 18，找了5个多小时QAQ 。

代码

#include <bits/stdc++.h>
#pragma comment(linker, "/STACK:102400000,102400000") 
using namespace std;
const int N=500005,M=N*4;
struct Gragh{
	//2M*2*4B+0.5M*4B=18MB
	int cnt,y[M],nxt[M],fst[N];
	void clear(){
		cnt=1;
		memset(fst,0,sizeof fst);
	}
	void add(int a,int b){
		y[++cnt]=b,nxt[cnt]=fst[a],fst[a]=cnt;
	}
}g,g2;
int n,m;
int dfn[N],low[N],inst[N],st[N],vis[N],id[N],Time,top,tot;
int used[M];
int Fa[N];
vector <int> cir[N],son[N];
void Tarjan_Prepare(){
	Time=top=tot=0;
	memset(id,0,sizeof id);
	memset(st,0,sizeof st);
	memset(dfn,0,sizeof dfn);
	memset(low,0,sizeof low);
	memset(vis,0,sizeof vis);
	memset(inst,0,sizeof inst);
	memset(used,0,sizeof used);
}
void Tarjan(int x){
	dfn[x]=low[x]=++Time;
	vis[x]=inst[x]=1;
	st[++top]=x;
	for (int i=g.fst[x];i;i=g.nxt[i]){
		if (used[i/2])
			continue;
		used[i/2]=1;
		if (!vis[g.y[i]]){
			Tarjan(g.y[i]);
			low[x]=min(low[x],low[g.y[i]]);
		}
		else if (inst[g.y[i]])
			low[x]=min(low[x],low[g.y[i]]);
	}
	if (dfn[x]==low[x]){
		tot++;
		id[st[top]]=tot;
		inst[st[top]]=0;
		while (st[top--]!=x){
			id[st[top]]=tot;
			inst[st[top]]=0;
		}
	}
}
void Get_cir(int x){
	if (vis[x])
		return;
	vis[x]=1;
	cir[id[x]].push_back(x);
	for (int i=g.fst[x];i;i=g.nxt[i]){
		int y=g.y[i];
		if (id[y]==id[x])
			Get_cir(y);
	}
}
void build(int x,int pre){
	int ID=id[x];
	Fa[ID]=pre;
	cir[ID].clear();
	Get_cir(x);
	for (int i=0;i<cir[ID].size();i++){
		int u=cir[ID][i];
		son[u].clear();
		for (int j=g.fst[u];j;j=g.nxt[j]){
			int v=g.y[j];
			if (id[v]==ID||id[v]==pre)
				continue;
			son[u].push_back(v);
			build(v,ID);
		}
	}
}
int Deep[N];
// The Minimum value of the distance between 
// x and the deepest posterity of x 
// 环根：   以该环为根的子树中，距离 x 最远的点与其距离的 最小值 
// 非环根： 该节点所有子节点（显然都是环根）的 Deep 最大值 + 1 
int spDeep[N],usDeep[N];
// spDeep[x] x 为环根，环边节点给他的贡献 
// usDeep[x] x 为环根，桥边子树给他的贡献 
int Lmax[N],Rmax[N];
void Get_Deep(int x){
	int ID=id[x];
	for (int i=0;i<cir[ID].size();i++){
		int u=cir[ID][i],v;
		Deep[u]=0;
		for (int j=0;j<son[u].size();j++){
			v=son[u][j];
			Get_Deep(v);
			Deep[u]=max(Deep[u],Deep[v]+1);
		}
	}
	int n=cir[ID].size()-1;
	Lmax[0]=Rmax[n+1]=0;
	for (int i=1;i<=n;i++)
		Lmax[i]=max(Lmax[i-1],Deep[cir[ID][i]]+i);
	for (int i=n;i>=1;i--)
		Rmax[i]=max(Rmax[i+1],Deep[cir[ID][i]]+(n-i+1));
	int v=1e9;
	for (int i=1;i<=n+1;i++)
		v=min(v,max(Lmax[i-1],Rmax[i]));
	Deep[x]=max(usDeep[x]=Deep[x],spDeep[x]=v);
}
int Far[N];
// The Minimum value of the distance between 
// x and the farthest vetrex which isn't a posterity of x 
// 环根：    由其父亲继承 
// 非环根：  环内单调队列跑出来 
int val[N*3];
int Lv[N*3],Rv[N*3];
struct Monotone_Queue{
	int head,tail,q[N*3],d[N*3];
	void clear(){
		head=1,tail=0;
	}
	int front(){
		return head<=tail?q[head]:-1e9;
	}
	void push(int v,int _d){
		while (head<=tail&&q[tail]<=v)
			tail--;
		q[++tail]=v,d[tail]=_d;
	}
	void pop(int _d){
		while (head<=tail&&d[head]<_d)
			head++;
	}
	int Next_front(int _d){
		if (head>tail)
			return -1e9;
		if (d[head]!=_d)
			return q[head];
		return head==tail?-1e9:q[head+1];
	}
}QL,QR;
vector <int> LRmax[N];
void Solve(int x,int far){
	int ID=id[x];
	Far[x]=far;
	int n=cir[ID].size();
	for (int i=1;i<n;i++)
		val[i]=Deep[cir[ID][i]];
	val[0]=max(usDeep[x],Far[x]);
	for (int i=n;i<n*3;i++)
		val[i]=val[i%n];
	for (int i=0;i<n*3;i++){
		Lv[i]=val[i]+n*3-i;
		Rv[i]=val[i]+i+1;
	}
	QL.clear(),QR.clear();
	int Lp=2,Rp=n+1;
	for (int i=Lp;i<=n;i++)
		QL.push(Lv[i],i);
	for (int i=n+1;i<n*2;i++){
		int result=1e9;
		int v1=n*3-i,v2=i+1;
		while (Rp<i){
			Lp++,QL.pop(Lp);
			Rp++;
			if (Rp!=i)
				QR.push(Rv[Rp],Rp);
		}
		while (QL.Next_front(Lp)-v1>max(QR.front(),Rv[Rp+1])-v2){
			result=min(result,QL.front()-v1);
			Lp++,QL.pop(Lp);
			Rp++,QR.push(Rv[Rp],Rp);
		}
		result=min(result,QL.front()-v1);
		result=min(result,max(QR.front(),Rv[Rp+1])-v2);
		QL.push(Lv[i],i);
		QR.pop(i+2);
		Far[cir[ID][i%n]]=result;
	}
	for (int i=0;i<n;i++){
		int u=cir[ID][i];
		int m=son[u].size();
		Lmax[0]=Rmax[m+1]=0;
		for (int j=1;j<=m;j++)
			Lmax[j]=max(Lmax[j-1],Deep[son[u][j-1]]+1);
		for (int j=m;j>=1;j--)
			Rmax[j]=max(Rmax[j+1],Deep[son[u][j-1]]+1);
		LRmax[u].clear();
		for (int j=0;j<m;j++)
			LRmax[u].push_back(max(Lmax[j],Rmax[j+2]));
		for (int j=0;j<m;j++)
			Solve(son[u][j],max(spDeep[u],max(Far[u],LRmax[u][j]))+1);
	}
}
int main(){
	scanf("%d%d",&n,&m);
	g.clear();
	for (int i=1,a,b;i<=m;i++){
		scanf("%d%d",&a,&b);
		g.add(a,b);
		g.add(b,a);
	}
	Tarjan_Prepare();
	for (int i=1;i<=n;i++)
		if (!vis[i])
			Tarjan(i);
	memset(vis,0,sizeof vis);
	build(1,0);
	Get_Deep(1);
	Solve(1,0);
	for (int i=1;i<=n;i++)
		printf("%d ",max(Far[i],Deep[i]));
	return 0;
}

　　

再放一份打满调试语句的代码：

#include <bits/stdc++.h>
#pragma comment(linker, "/STACK:102400000,102400000") 
using namespace std;
const int N=500005,M=N*4;
struct Gragh{
	//2M*2*4B+0.5M*4B=18MB
	int cnt,y[M],nxt[M],fst[N];
	void clear(){
		cnt=1;
		memset(fst,0,sizeof fst);
	}
	void add(int a,int b){
		y[++cnt]=b,nxt[cnt]=fst[a],fst[a]=cnt;
	}
}g,g2;
int n,m;
int dfn[N],low[N],inst[N],st[N],vis[N],id[N],Time,top,tot;
int used[M];
int Fa[N];
vector <int> cir[N],son[N];
void Tarjan_Prepare(){
	Time=top=tot=0;
	memset(id,0,sizeof id);
	memset(st,0,sizeof st);
	memset(dfn,0,sizeof dfn);
	memset(low,0,sizeof low);
	memset(vis,0,sizeof vis);
	memset(inst,0,sizeof inst);
	memset(used,0,sizeof used);
}
void Tarjan(int x){
	dfn[x]=low[x]=++Time;
	vis[x]=inst[x]=1;
	st[++top]=x;
	for (int i=g.fst[x];i;i=g.nxt[i]){
		if (used[i/2])
			continue;
		used[i/2]=1;
		if (!vis[g.y[i]]){
			Tarjan(g.y[i]);
			low[x]=min(low[x],low[g.y[i]]);
		}
		else if (inst[g.y[i]])
			low[x]=min(low[x],low[g.y[i]]);
	}
	if (dfn[x]==low[x]){
		tot++;
		id[st[top]]=tot;
		inst[st[top]]=0;
		while (st[top--]!=x){
			id[st[top]]=tot;
			inst[st[top]]=0;
		}
	}
}
void Get_cir(int x){
	if (vis[x])
		return;
	vis[x]=1;
	cir[id[x]].push_back(x);
	for (int i=g.fst[x];i;i=g.nxt[i]){
		int y=g.y[i];
		if (id[y]==id[x])
			Get_cir(y);
	}
}
void build(int x,int pre){
	int ID=id[x];
	Fa[ID]=pre;
	cir[ID].clear();
	Get_cir(x);
	for (int i=0;i<cir[ID].size();i++){
		int u=cir[ID][i];
		son[u].clear();
		for (int j=g.fst[u];j;j=g.nxt[j]){
			int v=g.y[j];
			if (id[v]==ID||id[v]==pre)
				continue;
			son[u].push_back(v);
			build(v,ID);
		}
	}
}
int Deep[N];
// The Minimum value of the distance between 
// x and the deepest posterity of x 
// 环根：   以该环为根的子树中，距离 x 最远的点与其距离的 最小值 
// 非环根： 该节点所有子节点（显然都是环根）的 Deep 最大值 + 1 
int spDeep[N],usDeep[N];
// spDeep[x] x 为环根，环边节点给他的贡献 
// usDeep[x] x 为环根，桥边子树给他的贡献 
int Lmax[N],Rmax[N];
void Get_Deep(int x){
	int ID=id[x];
	for (int i=0;i<cir[ID].size();i++){
		int u=cir[ID][i],v;
		Deep[u]=0;
		for (int j=0;j<son[u].size();j++){
			v=son[u][j];
			Get_Deep(v);
			Deep[u]=max(Deep[u],Deep[v]+1);
		}
	}
	int n=cir[ID].size()-1;
	Lmax[0]=Rmax[n+1]=0;
	for (int i=1;i<=n;i++)
		Lmax[i]=max(Lmax[i-1],Deep[cir[ID][i]]+i);
	for (int i=n;i>=1;i--)
		Rmax[i]=max(Rmax[i+1],Deep[cir[ID][i]]+(n-i+1));
	int v=1e9;
	for (int i=1;i<=n+1;i++)
		v=min(v,max(Lmax[i-1],Rmax[i]));
	Deep[x]=max(usDeep[x]=Deep[x],spDeep[x]=v);
}
int Far[N];
// The Minimum value of the distance between 
// x and the farthest vetrex which isn't a posterity of x 
// 环根：    由其父亲继承 
// 非环根：  环内单调队列跑出来 
int val[N*3];
int Lv[N*3],Rv[N*3];
struct Monotone_Queue{
	int head,tail,q[N*3],d[N*3];
	void clear(){
		head=1,tail=0;
	}
	int front(){
		return head<=tail?q[head]:-1e9;
	}
	void push(int v,int _d){
		while (head<=tail&&q[tail]<=v)
			tail--;
		q[++tail]=v,d[tail]=_d;
	}
	void pop(int _d){
		while (head<=tail&&d[head]<_d)
			head++;
	}
	int Next_front(int _d){
		if (head>tail)
			return -1e9;
		if (d[head]!=_d)
			return q[head];
		return head==tail?-1e9:q[head+1];
	}
	void print(){
		printf("size=%d, sit=:",tail-head+1);
		for (int i=head;i<=tail;i++)
			printf("(%d,%d)  ",q[i],d[i]);
		puts("");
	}
}QL,QR;
vector <int> LRmax[N];
void Solve(int x,int far){
	int ID=id[x];
	Far[x]=far;
	int n=cir[ID].size();
	for (int i=1;i<n;i++)
		val[i]=Deep[cir[ID][i]];
	val[0]=max(usDeep[x],Far[x]);
	for (int i=n;i<n*3;i++)
		val[i]=val[i%n];
	for (int i=0;i<n*3;i++){
		Lv[i]=val[i]+n*3-i;
		Rv[i]=val[i]+i+1;
	}
//	for (int i=0;i<n*3;i++)
//		printf("==>%d %d(%d) %d(%d)\n",val[i],Lv[i],n*3-i,Rv[i],i+1);
	QL.clear(),QR.clear();
	int Lp=2,Rp=n+1;
	for (int i=Lp;i<=n;i++)
		QL.push(Lv[i],i);
	for (int i=n+1;i<n*2;i++){
		int result=1e9;
		int v1=n*3-i,v2=i+1;
//		printf("i=%d,v1=%d,v2=%d\n",i,v1,v2);
		while (Rp<i){
			Lp++,QL.pop(Lp);
			Rp++;
			if (Rp!=i)
				QR.push(Rv[Rp],Rp);
		}
//		printf("x=%d,i=%d,Lp=%d,Rp=%d,Q=..(L,R)\n",x,i,Lp,Rp);QL.print(),QR.print();
		while (QL.Next_front(Lp)-v1>max(QR.front(),Rv[Rp+1])-v2){
			result=min(result,QL.front()-v1);
			Lp++,QL.pop(Lp);
			Rp++,QR.push(Rv[Rp],Rp);
		}
//		printf("x=%d,i=%d,Lp=%d,Rp=%d,Q=..(L,R)\n",x,i,Lp,Rp);QL.print(),QR.print();
		result=min(result,QL.front()-v1);
		result=min(result,max(QR.front(),Rv[Rp+1])-v2);
		QL.push(Lv[i],i);
		QR.pop(i+2);
		Far[cir[ID][i%n]]=result;
	}
	for (int i=0;i<n;i++){
		int u=cir[ID][i];
		int m=son[u].size();
		Lmax[0]=Rmax[m+1]=0;
		for (int j=1;j<=m;j++)
			Lmax[j]=max(Lmax[j-1],Deep[son[u][j-1]]+1);
		for (int j=m;j>=1;j--)
			Rmax[j]=max(Rmax[j+1],Deep[son[u][j-1]]+1);
/*		printf("u=%d,son=:",u);
		for (int j=0;j<m;j++)
			printf("%d ",son[u][j]);
		for (int i=1;i<=m;i++)
			printf ("(%d,%d) ",Lmax[i],Rmax[i]);puts("");*/
		LRmax[u].clear();
		for (int j=0;j<m;j++)
			LRmax[u].push_back(max(Lmax[j],Rmax[j+2]));
		for (int j=0;j<m;j++)
			Solve(son[u][j],max(spDeep[u],max(Far[u],LRmax[u][j]))+1);
	}
}
int main(){
	scanf("%d%d",&n,&m);
	g.clear();
	for (int i=1,a,b;i<=m;i++){
		scanf("%d%d",&a,&b);
		g.add(a,b);
		g.add(b,a);
	}
	Tarjan_Prepare();
	for (int i=1;i<=n;i++)
		if (!vis[i])
			Tarjan(i);
	memset(vis,0,sizeof vis);
//	for (int i=1;i<=n;i++)
//		printf("%d: %d\n",i,id[i]);
	build(1,0);
	Get_Deep(1);
	Solve(1,0);
/*	for (int i=1;i<=tot;i++,puts(""))
		for (int j=0;j<cir[i].size();j++)
			printf("%d ",cir[i][j]);*/
/*	for (int i=1;i<=n;i++){
		printf("%d:",i);
		for (int j=0;j<son[i].size();j++)
			printf(" %d",son[i][j]);
		puts("");
	}*/
/*	for (int i=1;i<=n;i++)
		printf("%d: %d %d %d %d\n",i,Deep[i],spDeep[i],usDeep[i],Far[i]);*/
	for (int i=1;i<=n;i++)
		printf("%d ",max(Far[i],Deep[i]));
	return 0;
}