Codeforces 947F. Public Service 构造
原文链接https://www.cnblogs.com/zhouzhendong/p/CF947F.html
近5K码量构造题,CF血腥残暴!
题解
这里先定义 $FT(k)$ 表示一个菊花树多 k 个点且这 k 个点都不在菊花的中心上。记 $C(x)$ 表示与 $x$ 直接相连的节点( x 为叶子的时候答案唯一)。
例如下面的一棵树就是一个 $FT(4)$ ,其中红色区域的是菊花,多出来的 4 个点在绿色区域。
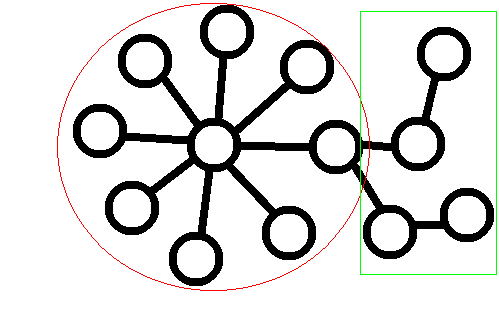
首先,这两棵树如果有任意一棵是 $FT(0)$ 则一定无解。因为如果有 $FT(0)$ 那么菊花中心的点的度数已经满了,在另一颗树中无论匹配什么点都不能有出边,GG。
否则,如果有任意一棵是 $FT(1)$ ,那么我们可以给出构造:
在另一棵树中找一个叶子 $b$,让菊花中心匹配它;假设 $FT(1)$ 中多出来的那个是节点 $a$,让它匹配 $C(b)$;让 $C(a)$ 找一个不与 $b$ 连通的节点对应(由于两棵树都不是 $FT(0)$ ,所以一定可以找到这样的节点);剩下的节点随便匹配。
否则,两棵树都至少是 $FT(2)$ 。考虑在第一棵树中分别找出两个叶子(设为u1,u2),保证这两个叶子的父亲不同且删除这两个叶子之后剩下的树不是 $FT(0)$ (由于这棵树至少是 $FT(2)$,所以必然存在一种方案),在第二棵树中也找出两个这样的点(设为v1,v2);在两棵树中分别删除选出的点,然后递归处理剩下的树的匹配;接下来考虑匹配(u1,v1) (u2,v2) 是否可行,假如不可行(就是 C(u1) 与 C(v1) 匹配了,或者 C(v2) 与 C(u2) 匹配了),那么交换 v1,v2,也就是匹配 (u1,v2) (u2,v1),简单画个图就可以证明这两种匹配中至少有一种是可行的。
对于点数小于等于 5 的,直接暴力枚举匹配就好了。
这样我们就找到了一种构造方法。
请您写一写这题代码。
祝您身体健康。
代码
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
using namespace std;
typedef long long LL;
LL read(){
LL x=0,f=0;
char ch=getchar();
while (!isdigit(ch))
f|=ch=='-',ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return f?-x:x;
}
const int N=10005;
int n;
map <int,int> mpa[N],mpb[N];
vector <int> a[N],b[N];
int p[N];
void Getp(vector <int> &A,vector <int> &B){
static int ga[10][10],gb[10][10],ya[N],yb[N];
clr(ga),clr(gb);
memset(ya,-1,sizeof ya);
memset(yb,-1,sizeof yb);
int m=A.size(),cnt=1;
for (int i=1;i<=m;i++)
cnt*=i;
for (int i=0;i<m;i++)
ya[A[i]]=i;
for (int i=0;i<m;i++)
yb[B[i]]=i;
for (int i=0;i<m;i++){
int x=A[i];
for (auto y : a[x])
if (ya[y]!=-1)
ga[i][ya[y]]=1;
}
for (int i=0;i<m;i++){
int x=B[i];
for (auto y : b[x])
if (yb[y]!=-1)
gb[i][yb[y]]=1;
}
vector <int> id(0);
for (int i=0;i<m;i++)
id.push_back(i);
while (cnt--){
int flag=1;
for (int i=0;i<m&&flag;i++)
for (int j=0;j<m&&flag;j++)
if (ga[i][j]&&gb[id[i]][id[j]])
flag=0;
if (flag){
for (int i=0;i<m;i++)
p[A[i]]=B[id[i]];
return;
}
next_permutation(id.begin(),id.end());
}
assert(0);
}
void vec_remove(vector <int> &v,int u){
int flag=0;
for (int i=0;i<(int)v.size();i++)
if (v[i]==u){
swap(v[i],v.back());
v.pop_back();
flag=1;
}
assert(flag);
}
vector <int> A,B;
int ctag[N];
int solve(){
A.clear(),B.clear();
int ra=0,rb=0;
for (int i=1;i<=n;i++){
if (!a[i].empty())
A.push_back(i);
if (!b[i].empty())
B.push_back(i);
if (a[i].size()>a[ra].size())
ra=i;
if (b[i].size()>b[rb].size())
rb=i;
}
int m=A.size();
if ((int)a[ra].size()+1==m||(int)b[rb].size()+1==m)
return 0;
if (m<=5)
return Getp(A,B),1;
if ((int)a[ra].size()+1==m-1){
int ai=0;
for (int i=0;i<m&&!ai;i++)
if (a[A[i]].size()==1&&a[A[i]][0]!=ra)
ai=A[i];
int bi=0;
for (int i=0;i<m&&!bi;i++)
if (b[B[i]].size()==1)
bi=B[i];
p[ra]=bi;
assert(!b[bi].empty());
int bf=p[ai]=b[bi][0];
int af=a[ai][0],afp=0;
vec_remove(A,ra);
vec_remove(A,ai);
vec_remove(B,bi);
vec_remove(B,bf);
clr(ctag);
for (auto by : b[bf])
ctag[by]=1;
for (int i=0;i<m-2&&!afp;i++)
if (!ctag[B[i]])
afp=B[i];
p[af]=afp;
vec_remove(A,af);
vec_remove(B,afp);
for (int i=0;i<m-3;i++)
p[A[i]]=B[i];
return 1;
}
if ((int)b[rb].size()+1==m-1){
int ai=0;
for (int i=0;i<m&&!ai;i++)
if (a[A[i]].size()==1)
ai=A[i];
int bi=0;
for (int i=0;i<m&&!bi;i++)
if (b[B[i]].size()==1&&b[B[i]][0]!=rb)
bi=B[i];
p[ai]=rb;
assert(!a[ai].empty());
p[a[ai][0]]=bi;
int af=a[ai][0];
int bf=b[bi][0],bfp=0;
vec_remove(B,rb);
vec_remove(B,bi);
vec_remove(A,ai);
vec_remove(A,af);
clr(ctag);
for (auto ay : a[af])
ctag[ay]=1;
for (int i=0;i<m-2&&!bfp;i++)
if (!ctag[A[i]])
bfp=A[i];
p[bfp]=bf;
vec_remove(B,bf);
vec_remove(A,bfp);
for (int i=0;i<m-3;i++)
p[A[i]]=B[i];
return 1;
}
int xa=0,ya=0,xb=0,yb=0;
int xza=0,yza=0,xzb=0,yzb=0;
for (int i=0;i<m&&!xa;i++)
if (a[A[i]].size()==1&&a[A[i]][0]!=ra)
xa=A[i];
if ((int)a[ra].size()+2==m-1){
for (int i=0;i<m&&!ya;i++)
if (a[A[i]].size()==1&&a[A[i]][0]==ra)
ya=A[i];
}
else {
for (int i=0;i<m;i++)
if (a[A[i]].size()==1&&(a[A[i]][0]!=ra||!ya)&&a[A[i]][0]!=a[xa][0])
ya=A[i];
}
for (int i=0;i<m&&!xb;i++)
if (b[B[i]].size()==1&&b[B[i]][0]!=rb)
xb=B[i];
if ((int)b[rb].size()+2==m-1){
for (int i=0;i<m&&!yb;i++)
if (b[B[i]].size()==1&&b[B[i]][0]==rb)
yb=B[i];
}
else {
for (int i=0;i<m;i++)
if (b[B[i]].size()==1&&(b[B[i]][0]!=rb||!yb)&&b[B[i]][0]!=b[xb][0])
yb=B[i];
}
xza=a[xa][0];
yza=a[ya][0];
xzb=b[xb][0];
yzb=b[yb][0];
#define rm vec_remove
#define rme(a,x,y) rm(a[x],y),rm(a[y],x)
rme(a,xa,xza);
rme(a,ya,yza);
rme(b,xb,xzb);
rme(b,yb,yzb);
#undef rme
#undef rm
int res=solve();
if (!res)
return 0;
if ((p[xza]==xzb&&mpa[xa][xza]&&mpb[xb][xzb])||(p[yza]==yzb&&mpa[ya][yza]&&mpb[yb][yzb]))
swap(xb,yb),swap(xzb,yzb);
assert(!(p[xza]==xzb&&mpa[xa][xza]&&mpb[xb][xzb])&&!(p[yza]==yzb&&mpa[ya][yza]&&mpb[yb][yzb]));
p[xa]=xb,p[ya]=yb;
return 1;
}
int main(){
n=read();
for (int i=1;i<n;i++){
int x=read(),y=read();
a[x].push_back(y);
a[y].push_back(x);
mpa[x][y]=mpa[y][x]=1;
}
for (int i=1;i<n;i++){
int x=read()-n,y=read()-n;
b[x].push_back(y);
b[y].push_back(x);
mpb[x][y]=mpb[y][x]=1;
}
int res=solve();
if (!res)
puts("No");
else {
puts("Yes");
for (int i=1;i<=n;i++)
printf("%d ",p[i]+n);
}
return 0;
}


