Codeforces 461D. Appleman and Complicated Task 构造,计数
原文链接https://www.cnblogs.com/zhouzhendong/p/CF461D.html
题解
首先我们可以发现如果确定了第一行,那么方案就唯一了。
然后,我们来看看一个点的值确定了会导致什么:

假设我们确定了红色点的值,那么所有包含橙色的格子xor起来就等于红色格子的值,绿色蓝色也是。
第一排就比较特殊了。
如果我们在对第一排奇偶分类之后,如果我们可以得到第一行的前缀xor之间的关系,那么我们就有希望解决这个问题。
再看一种情况:
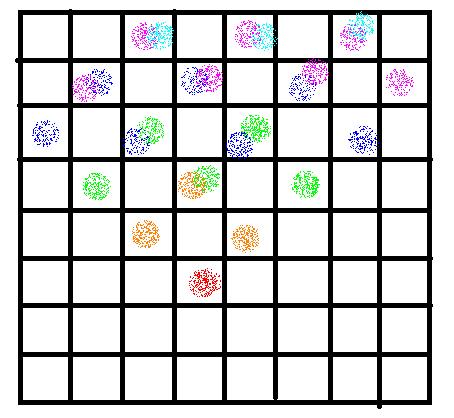
类似地意思,我们会发现这个东西遇到墙会反射。
于是我们就基本可以通过权值并查集来搞定。
我们还剩下一个问题:
这样的方式还不能确定最下面一行是否满足条件。
我们来看一个东西:
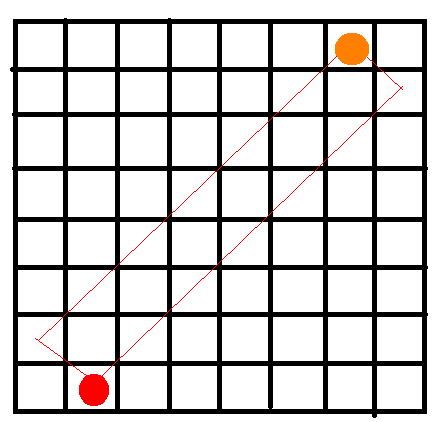
通过这个我们可以意识到,第一行和最后一行是一一对应的。于是整个局面旋转180度还是一样的。于是只要第一行合法,那么最后一行也合法。
所以我们只要通过给出的点用权值并查集维护一下第一行,然后算一下答案就好了。
代码
#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define For(i,a,b) for (int i=a;i<=b;i++)
#define Fod(i,b,a) for (int i=b;i>=a;i--)
using namespace std;
typedef long long LL;
LL read(){
LL x=0,f=0;
char ch=getchar();
while (!isdigit(ch))
f|=ch=='-',ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return f?-x:x;
}
const int N=100005,mod=1e9+7;
int n,k;
int fa[N],d[N];
int getf(int x){
if (fa[x]==x)
return x;
int f=getf(fa[x]);
d[x]^=d[fa[x]];
return fa[x]=f;
}
int Pow(int x,int y){
int ans=1;
for (;y;y>>=1,x=(LL)x*x%mod)
if (y&1)
ans=(LL)ans*x%mod;
return ans;
}
int main(){
n=read(),k=read();
For(i,0,n)
fa[i]=i;
while (k--){
int x=read(),y=read(),z;
char s[10];
scanf("%s",s);
z=s[0]=='x'?0:1;
int L=y-(x-1);
if (L<1)
L=1+(1-L);
int R=y+(x-1);
if (R>n)
R=n-(R-n);
L=max(0,L-2);
if (getf(L)!=getf(R))
d[fa[L]]=z^d[L]^d[R],fa[fa[L]]=fa[R];
else if (d[L]^d[R]^z)
return puts("0"),0;
}
int ans=-1;
For(i,0,n)
if (fa[i]==i)
ans++;
if (ans==-1)
assert(0);
cout<<Pow(2,ans)<<endl;
return 0;
}


