Codeforces Gym100543B 计算几何 凸包 线段树 二分/三分 卡常
原文链接https://www.cnblogs.com/zhouzhendong/p/CF-Gym100543B.html
题目传送门 - CF-Gym100543B
题意
给定一个折线图,对于每一条折线,问沿着这条折线往右看第一个看到的线段的编号(如果视线恰好看到上端点,则当没看见)
放张图片助于理解:
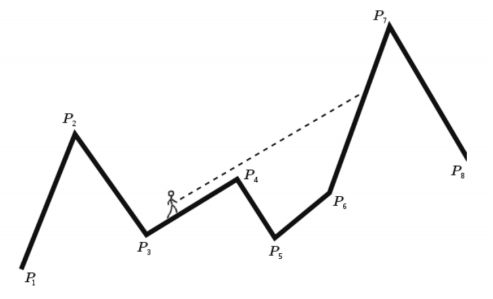
折线图用 $n$ 个点来描述。
$n\leq 100000,\ \ \ \ 坐标范围:(x,y)|0\leq x,y\leq 10^9$
题解
这题好妙啊。
首先一个结论:如果射线与一段区间的点形成的上凸壳相交,那么他一定与这段区间内的折线段相交。
我们只需要建个线段树,所有节点上建一个当前节点所表示的区间内的点构成的上凸壳,然后每次 $O(\log^2 n)$ 询问即可。
如何 $O(\log^2 n)$ 询问?
首先,线段树一只 $\log$ 。
我们需要支持的是一只 $\log$ 判断射线是否与上凸壳相交。
显然原线段与上凸壳的点的叉积是一个单峰函数。(根据叉积的定义,平行四边形的低不变,高为单峰函数,故面积也为单峰函数)
于是显然可以三分搞定。
但是被卡常数了。
于是 foreverpiano 告诉了我一种巧妙的二分做法。
(这里求叉积的点依次是线段左侧点,线段右侧点,当前点)
对于每一次的 $mid$ ,我们看一看 原线段与凸壳上面的第 $mid$ 和 $mid+1$ 个点的叉积大小,分别记为 $v1$ 和 $v2$。
如果 $v1>v2$ 则令 $R=mid-1$ 否则令 $L=mid+1$ 。
注意一旦有 $v1>0$ 或者 $v2>0$ 就可以判断一定相交了。如果这个时候不return,则可能会有漏算。
然后区间极小的时候暴力判。
然后常数小了好多。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=100005;
int T,n;
struct Point{
int x,y;
Point(){}
Point(int _x,int _y){
x=_x,y=_y;
}
}p[N],P[N];
vector <int> s[N<<3];
LL cross(Point a,Point b,Point c){
return 1LL*(b.x-a.x)*(c.y-a.y)-1LL*(c.x-a.x)*(b.y-a.y);
}
int read(){
char ch=getchar();
int x=0;
while (!isdigit(ch))
ch=getchar();
while (isdigit(ch))
x=(x<<1)+(x<<3)+ch-48,ch=getchar();
return x;
}
int st[N],top;
void Get_convex(vector <int> &s,int L,int R){
st[top=1]=R,st[++top]=R-1;
for (int i=R-2;i>=L;i--){
while (top>1&&cross(p[st[top-1]],p[st[top]],p[i])<=0)
top--;
st[++top]=i;
}
s.clear();
for (int i=top;i>0;i--)
s.push_back(st[i]);
}
void build(int rt,int L,int R){
if (L==R){
s[rt].clear();
s[rt].push_back(L);
return;
}
Get_convex(s[rt],L,R);
int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
build(ls,L,mid);
build(rs,mid+1,R);
}
int Query(Point a,Point b,vector <int> &s){
int L=0,R=s.size()-1,mid;
while (L+3<=R){
mid=(L+R)>>1;
LL x=cross(a,b,p[s[mid]]),y=cross(a,b,p[s[mid+1]]);
if (x>0||y>0)
return 1;
if (x>y)
R=mid-1;
else
L=mid+1;
}
int now=-1;
for (int i=L;i<=R;i++)
if (cross(a,b,p[s[i]])>0)
return 1;
return 0;
}
int Query(int rt,int L,int R,int xL,int xR){
if (xL>xR||L>xR||R<xL||!Query(p[xL-2],p[xL-1],s[rt]))
return 0;
if (L==R)
return L-1;
int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
int now=Query(ls,L,mid,xL,xR);
return now?now:Query(rs,mid+1,R,xL,xR);
}
int main(){
T=read();
while (T--){
n=read();
for (int i=1;i<=n;i++)
p[i].x=read(),p[i].y=read();
build(1,1,n);
for (int i=1;i<n;i++){
cout << Query(1,1,n,i+2,n);
if (i<n-1)
putchar(' ');
}
puts("");
}
return 0;
}


