BZOJ3153 sone1

原文链接www.cnblogs.com/zhouzhendong/p/BZOJ3153.html

题解

直接用splay维护虚子树。

细节真多。

暂时还不会证明。

可能是一个log或者两个log。

先咕一咕，等证明它挂了或者证明它是对的或者我弃疗不证明了再更新。

---

UPD(2019-04-10)：弃疗了证不出来不证了。只能证出复杂度上限是 $O(n\log ^2n)$ 的。14年论文里的 AAA-Tree 我也不会证，论文里也没有证明，我自闭了。

我来讲讲我的做法：

1. 结构

在 LCT 的基础上，对虚子树维护一个虚 splay 。

也就是说，一个节点可能有 5 种儿子：

real[x][0], real[x][1] 分别表示左实儿子 和 右实儿子。

virtson[x] 表示节点 x 的虚子树们的 splay ，不妨称它为 x 的虚儿子。

virt[x][0], virt[x][1] 表示节点 x 在虚 splay 中的左右儿子，不妨分别称他们为 x 的左虚儿子 和 右虚儿子。

注意 x 与它的左虚儿子和右虚儿子的关系，只代表他们有同一个父亲，且他们与这个父亲都只有虚边。

对于一个节点，它在 辅助树 中只有一个父亲。它的父亲可能有 4 种情况： 

　　1. 它是父亲的实儿子   2. 它是父亲的左虚儿子或者右虚儿子  3. 它是父亲的虚儿子  0. 它没有父亲

定义 father_kind(x) 函数表示节点 x 的父亲是哪一种。

那么，若 father_kind(x) = 1，则 x 没有左虚儿子和右虚儿子。

接下来，给出一张生动的图来更好的介绍一下这种结构。

注： 红色为实边，蓝色为虚左右儿子，绿色为虚儿子。加了红色喷雾标记的节点表示对应实链在原树上的最浅节点。

 

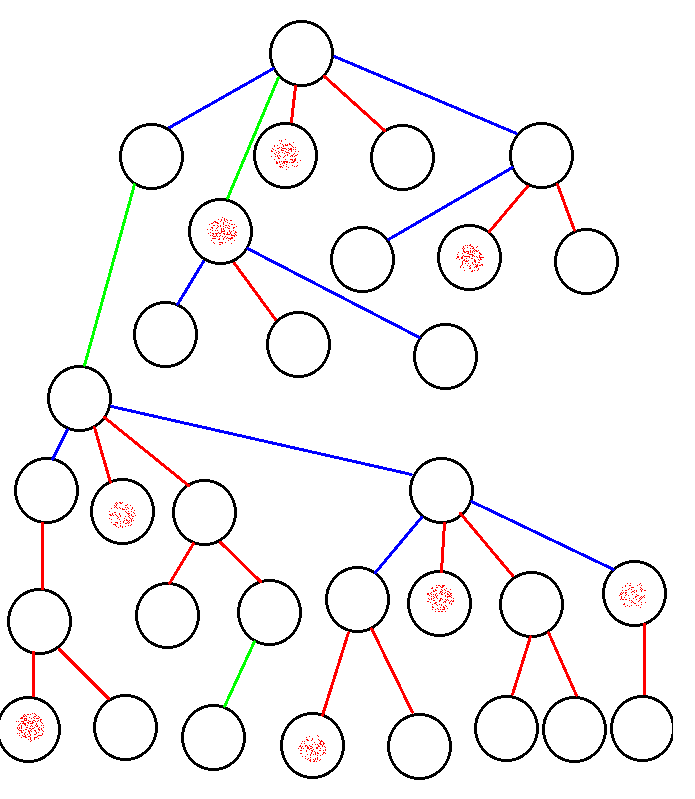
如果把实链的splay展开成链，那么会得到下图：

 

 

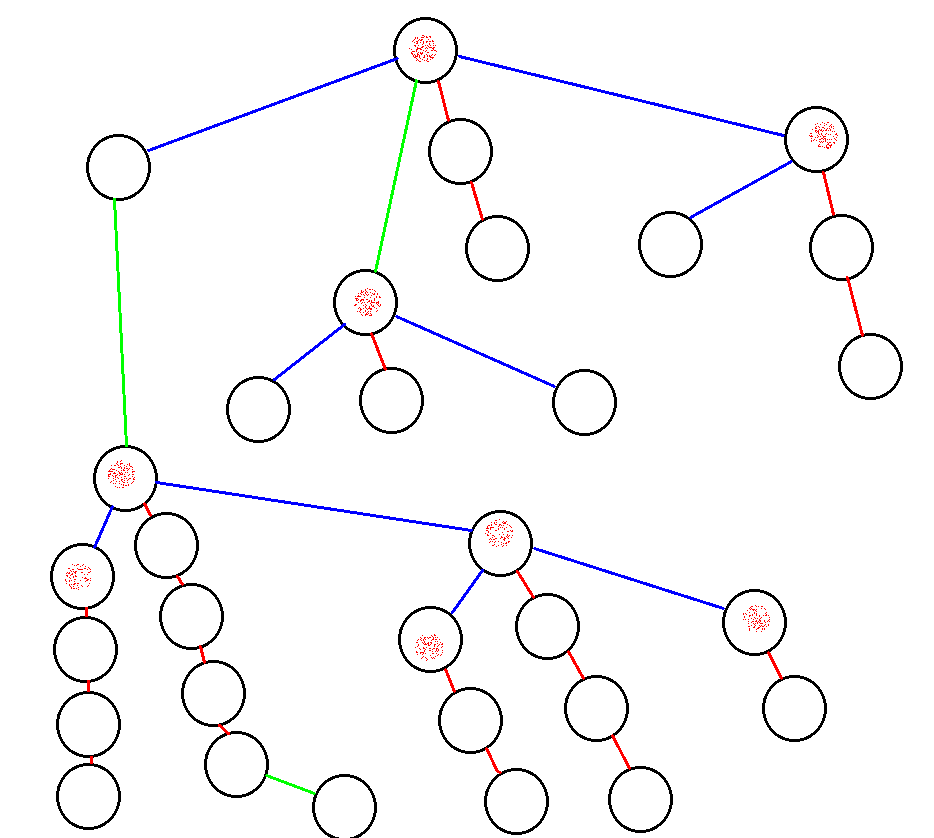
2. 旋转

相信从上面两幅图的比较中也可以发现一个事情：

在对实链进行旋转的时候，可能会改变节点的左右虚儿子：具体地，对于一个实splay，只有它的根这个位置有左右虚儿子。

而虚splay的根向上连的一定是一条绿色边。

所以我们得写两种旋转：rotate_real 和 rotate_virt 。

其中 rotate_real 的时候还要注意左右虚儿子的切换。

3. splay

splay 操作也是分成两个——splay_real 和 splay_virt ，但是没有什么区别。

4. access

和正常的 access 类似的思路，但是会比较麻烦。

4.1 kick

这个操作名没有什么含义，只是我自己随口说的，目的是为了照应代码中的函数名。

考虑到 LCT 需要进行虚实边切换，其中有一个操作是删除一个节点的右实儿子，换上某一个虚儿子。

kick函数的作用就是将一个节点的右实儿子踢出，扔进虚儿子里面。

4.2 接入新的实儿子

分两步：

把要接入的新节点从它所在的虚splay中删除；

接入到右实儿子的位置。

4.3 其他

注意到每组操作要splay两次，一次是splay_real，下一次是splay_virt 。

5. 构建初始的辅助树

比较简单不加介绍。

6. 信息的维护

定义一个信息包含两部分，分别是 实链信息 和 子树信息。

其中实链信息表示以它为根的实splay子树的信息。

子树信息表示 以它为根的实splay子树的所有节点的虚儿子 所在的子树的信息和它的虚儿子和它的左右虚儿子的信息。

如图所示：在这个结构中，橙色表示实链信息，紫色表示子树信息。

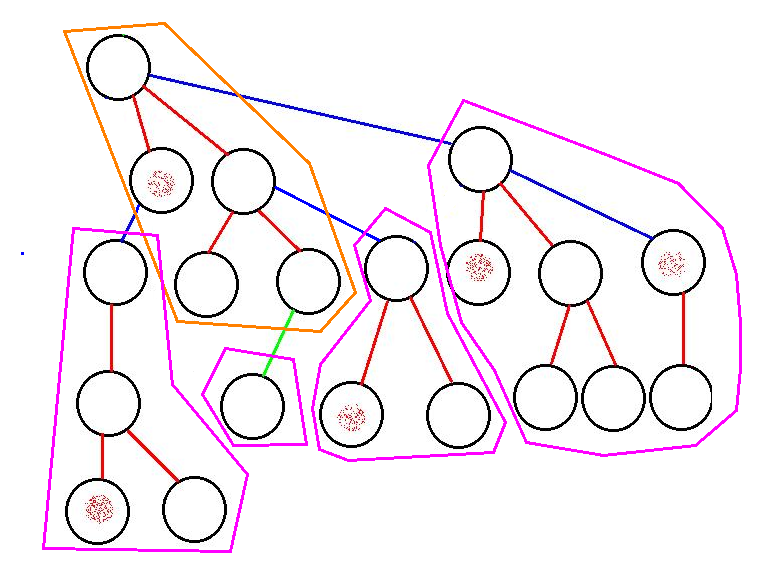
于是如何pushup就显而易见了。

如果让子树信息包含了实链信息，那么可能会在实现的时候出现意想不到的错误。我一开始就是这样做的，后来才发现出错了。具体为什么错？你试试就知道了。

 

我们需要维护 4 种信息：

Min：最小值信息

Max：最大值信息

sum：信息的和

size：信息的个数

 

7. 标记

如果说维护结构是这中做法的一个难点，那么标记的实现也是一个难点。而且它还有毒瘤细节。

标记我们也分成两类：实链标记和子树标记

实链标记、子树标记的作用范围的定义范围和实链信息、子树信息的定义范围分别对应。

但是实链标记和子树标记的作用是完全不同的。

实链标记用于修改实链，作用和普通 LCT 一样。

子树标记用于产生实链标记，每下传到一个新的实splay，就产生一个实链标记，而它本身不参与对值的修改。

具体地：子树标记往实儿子下传时，直接下传；往虚儿子和左右虚儿子下传时，下传子树标记的同时，对应产生一个实链标记。

 

我们需要维护两种标记：

add：标记-加

cov：标记-覆盖

其中，有一个比较容易忽略的细节：

在进行子树cov的时候，如果 cov 到的节点集合为空，那么不修改子树Min、Max信息。

 

还有一个标记是翻转标记，这个和 LCT 中的一样。

 

8. 换根

注意到，当我们有一个固定的根时，很多操作会很麻烦。

这里，一个技巧是：记录一个 true_root，在涉及子树操作时比较当前 root 是否等于 true_root，如果不等就换根。

9. 总结

通过做 sone1，我们可以再一次理解 LCT，并体会到这种要子树修改和换父亲的题在真实比赛中基本不可能写出来的趣味性。

代码

#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define For(i,a,b) for (int i=a;i<=b;i++)
#define Fod(i,b,a) for (int i=b;i>=a;i--)
#define pb(x) push_back(x)
#define mp(x,y) make_pair(x,y)
#define fi first
#define se second
#define real Real
#define _SEED_ ('C'+'L'+'Y'+'A'+'K'+'I'+'O'+'I')
#define outval(x) printf(#x" = %d\n",x)
#define outvec(x) printf("vec "#x" = ");for (auto _v : x)printf("%d ",_v);puts("")
#define outtag(x) puts("----------"#x"----------")
#define outarr(a,L,R) printf(#a"[%d...%d] = ",L,R);\
						For(_v2,L,R)printf("%d ",a[_v2]);puts("");
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef vector <int> vi;
LL read(){
	LL x=0,f=0;
	char ch=getchar();
	while (!isdigit(ch))
		f|=ch=='-',ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return f?-x:x;
}
const int N=100005,INF=0x7FFFFFFF;
int n,m,true_root,root;
struct Graph{
	static const int M=N*2;
	int cnt,y[M],nxt[M],fst[N];
	void clear(){
		cnt=1,clr(fst);
	}
	void add(int a,int b){
		y[++cnt]=b,nxt[cnt]=fst[a],fst[a]=cnt;
	}
}g;
int fa[N];
int val[N];
struct Tag{
	int c,t;
}Max[N],Min[N],sum[N],size[N],add[N],cov[N];
int rev[N];
int real[N][2],virt[N][2],virtson[N];
#define ls real[x][0]
#define rs real[x][1]
#define vls virt[x][0]
#define vrs virt[x][1]
#define vs virtson[x]
#define Mxt(x) max(Max[x].t,Max[x].c)
#define Mit(x) min(Min[x].t,Min[x].c)
#define sut(x) (sum[x].t+sum[x].c)
#define szt(x) (size[x].t+size[x].c)
void pushup_chain(int x){
	if (!x)
		return;
	Max[x].c=max(val[x],max(Max[ls].c,Max[rs].c));
	Min[x].c=min(val[x],min(Min[ls].c,Min[rs].c));
	sum[x].c=val[x]+sum[ls].c+sum[rs].c;
	size[x].c=size[ls].c+size[rs].c+1;
}
void pushup_tree(int x){
	if (!x)
		return;
	Max[x].t=max(max(Max[ls].t,Max[rs].t),max(Mxt(vs),max(Mxt(vls),Mxt(vrs))));
	Min[x].t=min(min(Min[ls].t,Min[rs].t),min(Mit(vs),min(Mit(vls),Mit(vrs))));
	sum[x].t=sum[ls].t+sum[rs].t+sut(vs)+sut(vls)+sut(vrs);
	size[x].t=size[ls].t+size[rs].t+szt(vs)+szt(vls)+szt(vrs);
}
void pushup(int x){
	if (x){
		pushup_chain(x);
		pushup_tree(x);
	}
}
int father_kind(int y){
	static int x;
	x=fa[y];
	if (ls==y||rs==y)
		return 1;// real
	else if (vls==y||vrs==y)
		return 2;// virt 
	else if (vs==y)
		return 3;// virt tree
	else
		return 0;// none(root)
}
int wson_real(int x){
	return real[fa[x]][1]==x;
}
int wson_virt(int x){
	return virt[fa[x]][1]==x;
}
void rotate_real(int x){
	int y=fa[x],z=fa[y],k=father_kind(y);
	if (k==1)
		real[z][wson_real(y)]=x;
	else if (k==2||k==3){
		if (k==2)
			virt[z][wson_virt(y)]=x;
		else
			virtson[z]=x;
		swap(virt[x][0],virt[y][0]);
		swap(virt[x][1],virt[y][1]);
	}
	// basical rotate
	int L=wson_real(x),R=L^1;
	fa[x]=z,fa[y]=x,fa[real[x][R]]=y;
	real[y][L]=real[x][R],real[x][R]=y;
	pushup(y),pushup(x);
}
void rotate_virt(int x){
	int y=fa[x],z=fa[y],k=father_kind(y);
	if (k==2)
		virt[z][wson_virt(y)]=x;
	else if (k==3)
		virtson[z]=x;
	// basical rotate 
	int L=wson_virt(x),R=L^1;
	fa[x]=z,fa[y]=x,fa[virt[x][R]]=y;
	virt[y][L]=virt[x][R],virt[x][R]=y;
	pushup(y),pushup(x);
}
void Cover_chain(int x,int v){
	if (!x)
		return;
	cov[x].c=v,add[x].c=0;
	val[x]=Min[x].c=Max[x].c=v;
	sum[x].c=v*size[x].c;
}
void Add_chain(int x,int v){
	if (!x)
		return;
	if (cov[x].c)
		cov[x].c+=v;
	else
		add[x].c+=v;
	val[x]+=v;
	Min[x].c+=v;
	Max[x].c+=v;
	sum[x].c+=v*size[x].c;
}
void Cover_tree(int x,int v){
	if (!x)
		return;
	cov[x].t=v,add[x].t=0;
	if (size[x].t)
		Min[x].t=Max[x].t=v;
	sum[x].t=v*size[x].t;
}
void Add_tree(int x,int v){
	if (!x)
		return;
	if (cov[x].t)
		cov[x].t+=v;
	else
		add[x].t+=v;
	Min[x].t=min((LL)INF,(LL)Min[x].t+v);
	Max[x].t+=v;
	sum[x].t+=size[x].t*v;
}
void Cover_All(int x,int v){
	Cover_chain(x,v);
	Cover_tree(x,v);
}
void Add_All(int x,int v){
	Add_chain(x,v);
	Add_tree(x,v);
}
void Reverse(int x){
	if (!x)
		return;
	swap(ls,rs),rev[x]^=1;
}
void pushdown(int x){
	if (!x)
		return;
	if (rev[x]){
		Reverse(ls);
		Reverse(rs);
		rev[x]=0;
	}
	if (cov[x].c){
		Cover_chain(ls,cov[x].c);
		Cover_chain(rs,cov[x].c);
	}
	else if (add[x].c){
		Add_chain(ls,add[x].c);
		Add_chain(rs,add[x].c);
	}
	if (cov[x].t){
		Cover_All(vs,cov[x].t);
		Cover_All(vls,cov[x].t);
		Cover_All(vrs,cov[x].t);
		Cover_tree(ls,cov[x].t);
		Cover_tree(rs,cov[x].t);
	}
	else if (add[x].t){
		Add_All(vs,add[x].t);
		Add_All(vls,add[x].t);
		Add_All(vrs,add[x].t);
		Add_tree(ls,add[x].t);
		Add_tree(rs,add[x].t);
	}
	cov[x].c=cov[x].t=add[x].c=add[x].t=0;
}
void pushadd(int x,int k){
	if (father_kind(x)==k)
		pushadd(fa[x],k);
	pushdown(x);
}
void splay_real(int x){
	pushadd(x,1);
	for (int y=fa[x];father_kind(x)==1;rotate_real(x),y=fa[x])
		if (father_kind(y)==1)
			rotate_real(wson_real(x)==wson_real(y)?y:x);
}
void splay_virt(int x){
	pushadd(x,2);
	for (int y=fa[x];father_kind(x)==2;rotate_virt(x),y=fa[x])
		if (father_kind(y)==2)
			rotate_virt(wson_virt(x)==wson_virt(y)?y:x);
}
void access_push_add(int x){
	if (fa[x])
		access_push_add(fa[x]);
	pushdown(x);
}
int Merge(int x,int y){
	if (!x||!y)
		return x+y;
	pushdown(x);
	pushdown(y);
	if (size[x].t<size[y].t)
		swap(x,y);
	if (y)
		fa[y]=x;
	if (size[virt[x][0]].t<size[virt[x][1]].t)
		virt[x][0]=Merge(virt[x][0],y);
	else
		virt[x][1]=Merge(virt[x][1],y);
	pushup(x);
	return x;
}
void kick(int x){
	if (rs){
		int y=rs,z=virtson[x];
		pushdown(y);
		virt[y][0]=z;
		fa[z]=y,fa[y]=x;
		virtson[x]=y;
		rs=0;
		pushup(y),pushup(x);
	}
}
void access(int x){
	int t=0;
	access_push_add(x);
	while (x){
		splay_real(x);
		splay_virt(x);
		kick(x);
		int y=fa[x];
		if (t){
			rs=t,fa[t]=x;
			pushup(x);
		}
		int z=Merge(vls,vrs);
		if (y)
			virtson[y]=z;
		fa[z]=y,fa[x]=0;
		vls=vrs=0;
		pushup(y);
		t=x,x=y;
	}
}
void rever(int x){
	access(x);
	splay_real(x);
	Reverse(x);
	root=x;
}
void check_root(){
	if (root!=true_root)
		rever(true_root);
}
void cut(int x){
	check_root();
	access(x);
	splay_real(x);
	fa[ls]=0,ls=0;
	pushup(x);
}
void link(int x,int y){
	rever(x),access(y),splay_real(y);
	real[y][1]=x;
	fa[x]=y;
	pushup(y);
	root=y;
	while (real[root][0])
		root=real[root][0];
}
void dfs(int x,int pre){
	int pre_son=0;
	for (int i=g.fst[x];i;i=g.nxt[i]){
		int y=g.y[i];
		if (y!=pre){
			dfs(y,x);
			if (!pre_son)
				pre_son=y;
			else {
				fa[pre_son]=y;
				virt[y][0]=pre_son;
				pre_son=y;
			}
			pushup(y);
		}
	}
	if (pre_son)
		fa[pre_son]=x,vs=pre_son;
	pushup(x);
}
void set_tree(int x){
	check_root();
	access(x);
	splay_real(x);
}
void set_chain(int x,int y){// finally y in top
	rever(x);
	access(y);
	splay_real(y);
}
int main(){
	n=read(),m=read();
	g.clear();
	For(i,1,n-1){
		int x=read(),y=read();
		g.add(x,y),g.add(y,x);
	}
	For(i,1,n)
		val[i]=read();
	root=true_root=read();
	Min[0].c=Min[0].t=INF,Max[0].c=Max[0].t=-INF-1;
	dfs(root,0);
	while (m--){
		int type=read();
		if (type==0){
			int x=read(),y=read();
			set_tree(x);
			Cover_All(rs,y);
			Cover_All(vs,y);
			val[x]=y;
			pushup(x);
		}
		else if (type==1){
			int x=read();
			true_root=x;
		}
		else if (type==2){
			int x=read(),y=read(),z=read();
			set_chain(x,y);
			Cover_chain(y,z);
		}
		else if (type==3){
			int x=read();
			set_tree(x);
			printf("%d\n",min(val[x],min(Mit(vs),Mit(rs))));
		}
		else if (type==4){
			int x=read();
			set_tree(x);
			printf("%d\n",max(val[x],max(Mxt(vs),Mxt(rs))));
		}
		else if (type==5){
			int x=read(),y=read();
			set_tree(x);
			Add_All(rs,y);
			Add_All(vs,y);
			val[x]+=y;
			pushup(x);
		}
		else if (type==6){
			int x=read(),y=read(),z=read();
			set_chain(x,y);
			Add_chain(y,z);
		}
		else if (type==7){
			int x=read(),y=read();
			set_chain(x,y);
			printf("%d\n",Min[y].c);
		}
		else if (type==8){
			int x=read(),y=read();
			set_chain(x,y);
			printf("%d\n",Max[y].c);
		}
		else if (type==9){
			int x=read(),y=read();
			if (x!=y){
				check_root();
				access(y),splay_real(y);
				int z=x;
				while (father_kind(z)==1)
					z=fa[z];
				if (z!=y){
					cut(x);
					link(x,y);
				}
			}
		}
		else if (type==10){
			int x=read(),y=read();
			set_chain(x,y);
			printf("%d\n",sum[y].c);
		}
		else if (type==11){
			int x=read();
			set_tree(x);
			printf("%d\n",val[x]+sut(vs)+sut(rs));
		}
	}
	return 0;
}