差分约束系统学习笔记

差分约束系统：

1.算法用途：

解决形如这样一组不等式：

\[\left\{\begin{matrix}x_{1}-x_{2}\leq 0 \\ x_{1}-x_{5}\leq 1 \\ x_{2}-x_{5}\leq 1 \\ x_{3}-x_{1}\leq 5 \\ x_{4}-x_{1}\leq 4 \\ x_{4}-x_{3}\leq -1 \\ x_{5}-x_{3}\leq -3 \\ x_{5}-x_{4}\leq -3 \end{matrix}\right.\]

这种不等式的特点是：

1.都是两个数的差小于等于某个常数（当然大于等于也可以，因为两边同时乘以-1也可以化为小于等于的形式）。

2.要么无解，要么就有无限组解。

 

2.算法与单源最短路径的联系：

1.三角形不等式：

在单源最短路径问题中，任意一条边都满足一个三角形不等式：

\[dis[u]\leq dis[v]+len[u][v]\]

 

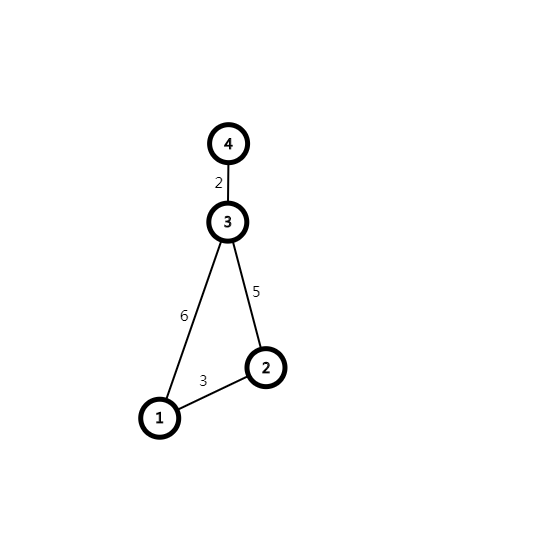
例：

在上面这幅图中，满足

\[dis[3]\leq dis[2]+len[2][3]\]

 

 

2.差分约束系统也正好满足于这个条件，所以可以用单源最短路径来解决差分约束系统。

 

3.算法实现步骤：

每个不等式的未知数都可以给它一个节点

对于每一个不等式：

\[x_{i}-x_{j}\leq y\]

可以化为：

\[x_{i}\leq x_{j}+y\]

所以我们给

\[i,j\]

这两个点建一条边权为y的边

例：

\[\left\{\begin{matrix}x_{1}-x_{2}\leq 0 \\ x_{1}-x_{5}\leq 1 \\ x_{2}-x_{5}\leq 1 \\ x_{3}-x_{1}\leq 5 \\ x_{4}-x_{1}\leq 4 \\ x_{4}-x_{3}\leq -1 \\ x_{5}-x_{3}\leq -3 \\ x_{5}-x_{4}\leq -3 \end{matrix}\right.\]

可以构图：

 

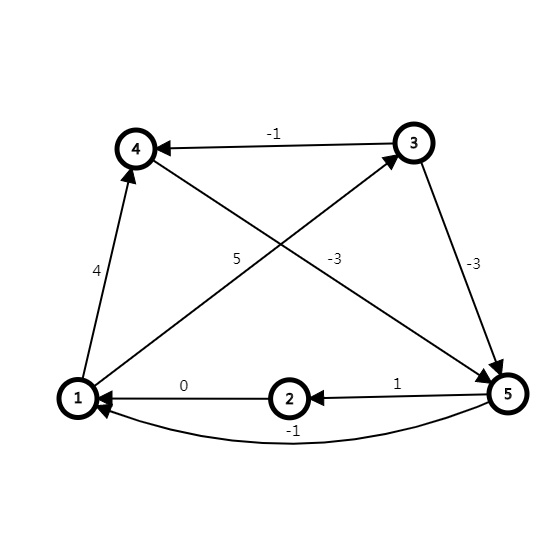
然后我们可以从每个点出发跑一遍最短路

虽然每次会得到不同的解，但是这些解每个都是可行的。

但是我们要得到统一的解，所以我们可以增加一个源点0

可是这与差分约束系统又有什么关系呢？？？

我们不妨增加一个不等式：

\[\left\{\begin{matrix}x_{1}-x_{0}\leq 0 \\ x_{2}-x_{0}\leq 0 \\ x_{3}-x_{0}\leq 0 \\ x_{4}-x_{0}\leq 0 \\ x_{5}-x_{0}\leq 0 \end{matrix}\right.\]

这时图可以变成：

 

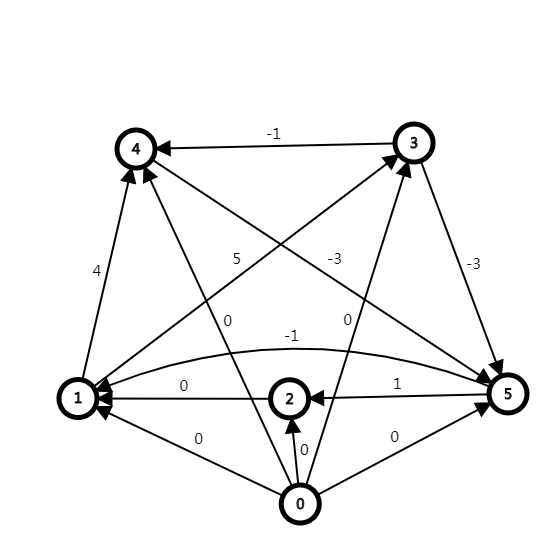
这时我们便可以从源点0开始，跑一遍单源最短路径

当然如果要求不等式的最大解，可以把最短路改为最长路。

当我们把初值

\[dis[0]=X\]

所有未知数的解都不会大于X（但我们一般都会把这个dis[0]设为0）