斜率优化：
1.算法用途：用于优化一些DP形如的式子：
![f[j]-f[k]<kx+b](http://latex.codecogs.com/gif.latex?f%5Bj%5D-f%5Bk%5D%3Ckx+b)
2.算法步骤：（例题：
）链接
1.推出DP方程式：![f[i]=min(f[j]+(sum[i]-sum[j-1])^{2}+M)(j<i)](http://latex.codecogs.com/gif.latex?f%5Bi%5D%3Dmin%28f%5Bj%5D+%28sum%5Bi%5D-sum%5Bj-1%5D%29%5E%7B2%7D+M%29%28j%3Ci%29)
2.设在求
时从
转移比从
转移更优
3.写出一个不等式![f[j]+(sum[i]-sum[j-1])^{2}+M<f[k]+(sum[i]-sum[k-1])^{2}+M](http://latex.codecogs.com/gif.latex?f%5Bj%5D+%28sum%5Bi%5D-sum%5Bj-1%5D%29%5E%7B2%7D+M%3Cf%5Bk%5D+%28sum%5Bi%5D-sum%5Bk-1%5D%29%5E%7B2%7D+M)
4.拆开移项合并同类项：![f[j]-f[k]<2sum[i](sum[j-1]-sum[k-1])+sum[k-1]^{2}-sum[j-1]^{2}](http://latex.codecogs.com/gif.latex?f%5Bj%5D-f%5Bk%5D%3C2sum%5Bi%5D%28sum%5Bj-1%5D-sum%5Bk-1%5D%29+sum%5Bk-1%5D%5E%7B2%7D-sum%5Bj-1%5D%5E%7B2%7D)
（形如
）
5.继续变形变成：![(f[j]-f[k]+sum[j-1]^2-sum[k-1]^2)/(2*(sum[j-1]-sum[k-1]))<sum[i]](http://latex.codecogs.com/gif.latex?%28f%5Bj%5D-f%5Bk%5D+sum%5Bj-1%5D%5E2-sum%5Bk-1%5D%5E2%29/%282*%28sum%5Bj-1%5D-sum%5Bk-1%5D%29%29%3Csum%5Bi%5D)
6.设![xi=f[i]+sum[i-1]^2](http://latex.codecogs.com/gif.latex?xi%3Df%5Bi%5D+sum%5Bi-1%5D%5E2)
，![yi=sum[i-1]*2](http://latex.codecogs.com/gif.latex?yi%3Dsum%5Bi-1%5D*2)
7.则原式可以写成：![(xj-xk)/(yj-yk)=sum[i]](http://latex.codecogs.com/gif.latex?%28xj-xk%29/%28yj-yk%29%3Dsum%5Bi%5D)
8.因为![sum[i]](http://latex.codecogs.com/gif.latex?sum%5Bi%5D)
呈单调性，所以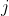
的转移一定比
优（见下图）
9.这其实是下凹凸包（链接1：大佬博客）（链接2：百度百科）
10.所以可以用一个单调队列，过程如下：
11.一直往下，直到解比队尾更优
12.所以开始的时候直接从队头开始进行DP
小结：
1.要先想出DP方程式
2.写出不等式
3.根据题意化简变为斜率优化的样子
.jpg)
