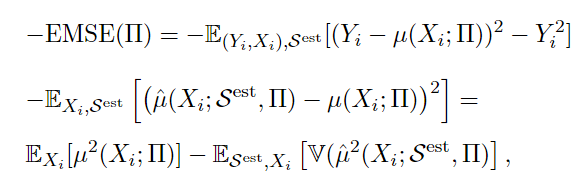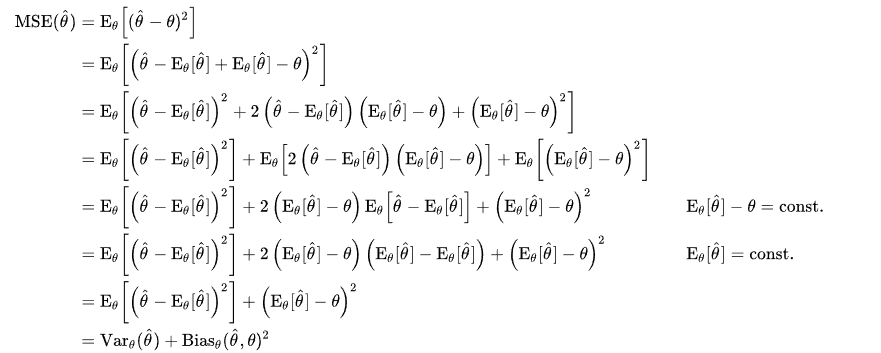Tree-Based Algorithms
Tree-based这类方法,和之前meta-learning 类的方法最明显的区别是: 这类方法把causal effect 的计算显示的加入了到了树模型节点分裂的标准中 从 response时代过渡到了effect时代。
大量的这类算法基本围绕着树节点分裂方式做文章,普遍采用的是兼容性比较高的[[万字长文讲述树模型的历史|cart树]]
Causal Tree & Honest Tree
causal tree[4] 这篇文章算是较早通过改变树模型node分裂方式来预估[[因果推断及其重要相关概念#heterogeneous causal effects|异质因果效应]](heterogeneous causal effects)的算法。
所以重点还是如何去构建 split criterion,前置可能要说一下相关的符号含义:
在特征空间 \(\mathbb X\) 下存在节点分裂方式的集合:
\[\prod(\ell_1,...,\ell_{\#(T)})
\]
其中以 \(\ell(x;\prod)\) 表示叶子节点\(\ell\) 属于划分方式 \(\prod\), 此时该划分方式下的,node的条件期望定义为:
\[\mu(x;\prod)=E[Y_i|X_i \in \ell(x;\prod)]
\]
那么,自然如果给定样本\(S\) , 其对应节点无偏统计量为:
\[\hat \mu(x;S,\prod)=\frac{1}{\#(i\in S: X_i \in \ell(x;\prod))}\sum_{i\in S:X_i\in\ell_i(x;\prod)} Y_i
\]
Causal Tree 学习的目标 or loss func
学习目标使用修改后的MSE, 在标准mse的基础上多减去了一项和模型参数估计无关的\(E[Y^2]\),此外
训练即build tree阶段,train set被切为两部分,一部分训练样本train set:\(S^{tr}\) , 一部分是估计样本 est set \(S^{est}\),还有测试样本test set \(S^{te}\)
这里有点绕:和经典的树模型不一样的是:叶子节点上存储的值不是根据train set来的, 而是划分好之后通过est set进行估计。(显然, 这种方式有点费样本...)。所以,这也是文中为啥把这种方法叫做“Honest”的原因。
假设已经根据训练样本得到划分方式,那么评估这种划分方式好坏被定义为:
\[MSE(S^{te}, S^{est},\prod)=\frac{1}{\#(S^{te})} \sum_{i\in S^{te}} \{(Y_i-\hat\mu(X_i;S^{est},\prod))^2-Y_i^2\}
\]
整体求期望变成:
\[EMSE(\prod)=E_{S^{te},S^{est}}[MSE(S^{te}, S^{est},\prod)]
\]
算法的整体目标为:
\[Q^{H}(\pi)=-E_{S^{est}, S^{est}, S^{tr}}[MSE(S^{te}, S^{est},\pi(S^{tr}))]
\]
其中,\(\pi(S)\) 定义为:
\[\pi(\mathcal{S})= \begin{cases}\{\{L, R\}\} & \text { if } \bar{Y}_L-\bar{Y}_R \leq c \\ \{\{L\},\{R\}\} & \text { if } \bar{Y}_L-\bar{Y}_R>c .\end{cases}
\]
其实就是比较节点在划分后,左右子节点的输出差异是否满足阈值c,\(\bar Y_L=\mu(L)\)
节点划分方式
作者直接给出了节点划分时的loss计算标准:
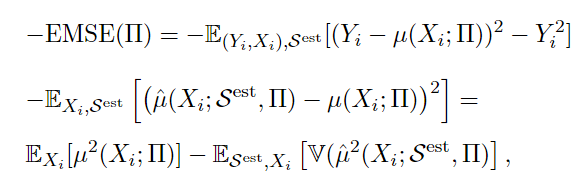
我们来推导一下:
\[\begin{aligned}
EMSE(\small\prod)&=E_{S^{te},S^{est}}[\frac{1}{\#(S^{te})} \sum_{i\in S^{te}} \{(Y_i-\hat\mu(X_i;S^{est},\small\prod))^2-Y_i^2\}] \\
&=E_{S^{te},S^{est}}[(Y_i-\hat\mu(X_i;S^{est},\small\prod))^2-Y_i^2] \\
&=E_{S^{te},S^{est}}[(Y_i-\mu(X_i;\small\prod)+\mu(X_i;\small\prod)-\hat\mu(X_i;S^{est},\small\prod))^2 - Y_i^2] \\
&=E_{S^{te},S^{est}}[\{Y_i-\mu(X_i;\small\prod)\}^2-Y_i^2] \\
&+2E_{S^{te},S^{est}}[\{Y_i-\mu(X_i;\small\prod)\}\{(\mu(X_i;\small\prod)-\hat\mu(X_i;S^{est},\small\prod)\}] \\
&+E_{S^{te},S^{est}}[\{\mu(X_i;\small\prod)-\hat\mu(X_i;S^{est},\small\prod)\}^2]
\end{aligned}
\]
因为中间展开项期望为0, 所以公式变成:
\[\begin{aligned}
EMSE(\small\prod)&=E_{S^{te},S^{est}}[\{Y_i-\mu(X_i;\small\prod)\}^2-Y_i^2]+E_{S^{te},S^{est}}[\{\mu(X_i;\small\prod)-\hat\mu(X_i;S^{est},\small\prod)\}^2] \\
&=E_{S^{te},S^{est}}[(\mu(X_i;\small\prod))^2-2Y_i\mu(X_i;\small\prod)]+E_{S^{te},S^{est}}[\{\mu(X_i;\small\prod)-\hat\mu(X_i;S^{est},\small\prod)\}^2]
\end{aligned}
\]
同样的,展开项的项期望为0,由于无偏估计=> \(\mu(X_i;\small \prod)=E_{S^{est}}[\hat \mu(X_i;S^{est};\small\prod)]\) ,最终公式变成:
\[-EMSE(\small\prod)=E_{X_i}[\mu^2(X_i;\small \prod)]-E_{S^{est},X_i}[\mathbb V(\hat\mu(X_i;S^{est}, \small\prod))]
\]
其中,\(E_{S^{est},X_i}[\mathbb V(\hat\mu(X_i;S^{est}, \small\prod))]=E_{S^{te},S^{est}}[\{\hat\mu(X_i;S^{est},\small\prod)-\mu(X_i;\small\prod\}^2]\)
公式中第一项可以理解为偏差的平方,第二项理解为方差。为什么MSE可以被理解成偏差和方差的组合,以及展开项为0
我们来证明一下:(开个玩笑:),其实我是抄的Wikipedia,可以看证明1和证明2:
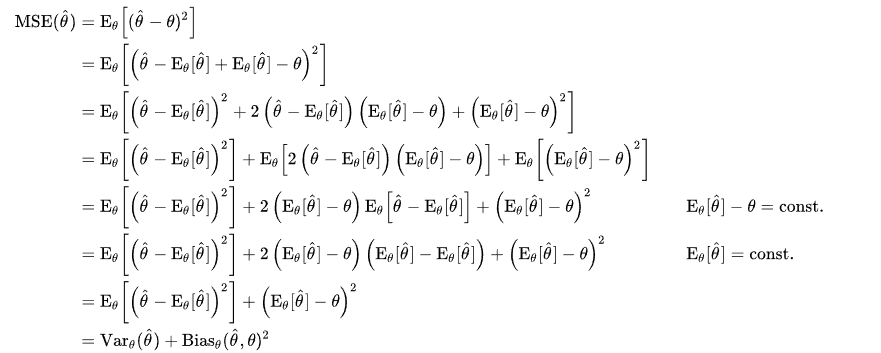
偏差项
接着分析偏差项:
\[\begin{aligned}
E_{X_i}\left[\mu^2\left(X_i ; \Pi\right)\right] & =E_{X_i}\left\{\left[E_S\left(\hat{\mu}\left(X_i ; S, \Pi\right)\right)\right]^2\right\} \\
& =E_{X_i}\left\{E_S\left[\hat{\mu}^2\left(X_i ; S, \Pi\right)\right]-\mathbb V_S\left[\hat{\mu}\left(X_i ; S, \Pi\right)\right]\right\} \\
& =E_{X_i}\left\{E_S\left[\hat{\mu}^2\left(X_i ; S, \Pi\right)\right]\right\}-E_{X_i}\left\{\mathbb V_S\left[\hat{\mu}\left(X_i ; S, \Pi\right)\right]\right\}
\end{aligned}
\]
第一项总体估计值的期望使用训练集的样本,即:
\[\hat \mu^2(X_i;S^{tr},\small \prod)=E_S[\hat\mu^2(X_i;S;\small\prod)]
\]
第二项方差项,叶子节点方差求均值
\[\mathbb V_S[\hat\mu^2(X_i;S;\small\prod)]=\frac{S_{S^{tr}}^2}{N^{tr}}
\]
对于最外层的期望:
\[\begin{aligned}
\hat{E}_{X_i}\left[\mu^2\left(X_i ; \Pi\right)\right] & =\sum_{l \in \Pi} \frac{N_l^{t r}}{N^{t r}} \hat{\mu}^2\left(X_i ; S^{t r}, \Pi\right)-\sum_{l \in \Pi} \frac{N_l^{t r}}{N^{t r}} \frac{S_{t r}^2[\ell(x, \Pi)]}{N_\ell^{t r}} \\
& =\frac{1}{N^{t r}} \sum_{i \in S^{t r}} \hat{\mu}^2\left(X_i ; S^{t r}, \Pi\right)-\frac{1}{N^{t r}} \sum_{\ell \in \Pi} S_{t r}^2[\ell(x, \Pi)]
\end{aligned}
\]
方差项
\[\mathbb V(\hat\mu(X_i;S^{est}, \small\prod)=\frac{S_{S^{tr}}^{2}(\ell(x;\small \prod)}{N^{est}(\ell(x;\small \prod))}
\]
\[E_{S^{est},X_i}[\mathbb{V}\left(\hat{\mu}^2\left(X_i ; \mathcal{S}^{\text {est }}, \Pi\right) \mid i \in \mathcal{S}^{\text {te }}\right] \equiv \frac{1}{N^{\text {est }}} \cdot \sum_{\ell \in \Pi} S_{\mathcal{S}^{\text {tr }}}^2(\ell)
\]
整合
最终估计量为:
\[-\hat{EMSE(S^{tr},\small \prod)}=\frac{1}{N^{\operatorname{tr}}} \sum_{i \in \mathcal{S}^{\mathrm{tr}}} \hat{\mu}^2\left(X_i ; \mathcal{S}^{\operatorname{tr}}, \Pi\right)-\left(\frac{1}{N^{\operatorname{tr}}}+\frac{1}{N^{\mathrm{est}}}\right) \cdot \sum_{\ell \in \Pi} S_{\mathcal{S}^{\operatorname{tr}}}^2(\ell)
\]
\[=\frac{1}{N^{\operatorname{tr}}} \sum_{i \in \mathcal{S}^{\operatorname{tr}}} \hat{\mu}^2\left(X_i ; \mathcal{S}^{\operatorname{tr}}, \Pi\right)-\frac{2}{N^{\operatorname{tr}}} \cdot \sum_{\ell \in \Pi} S_{\mathcal{S}^{\operatorname{tr}}}^2(\ell)
\]
其中, 偏差和方差不过的est估计量应该用est set,但是此处假设了train set和est set 同分布。
treatment effect 介入划分:处理异质效应
前面定义了MSE的范式,当需要考虑到异质效应时,定义异质效应:
\[\tau = \mu(1, x;\small\prod)-\mu(0;x;\small \prod)
\]
很显然,我们永远观测不到异质性处理效应,因为我们无法观测到反事实,我们只能够估计处理效应,给出异质性处理效应的估计量:
\[\hat \tau(w,x;S,\small \prod)=\hat \tau(1,s;S,\small \prod)-\hat \tau(0,s;S,\small \prod)
\]
因果效应下的EMSE为:
\[MSE_{\tau}=\frac{1}{\#(S^{te})}\sum_{i\in S^{te}} \{(\tau_i-\hat \tau(Xi;S^{est},\small \prod))^2-\tau_i^2\}
\]
\[-\operatorname{EMSE}_\tau(\Pi)=\mathbb{E}_{X_i}\left[\tau^2\left(X_i ; \Pi\right)\right]-\mathbb{E}_{\mathcal{S}^{\text {est }}, X_i}\left[\mathbb{V}\left(\hat{\tau}^2\left(X_i ; \mathcal{S}^{\text {est }}, \Pi\right)\right]\right.
\]
使用\(\tau\)替代了\(\mu\) , 偏差项, 带入整合公式:
\[-\hat {EMSE_{\tau}(S^{tr, \small\prod})}=\frac{1}{N^{tr}}\sum_{i\in S^{tr}} \hat \tau^2(Xi;S^{tr},\small \prod)-\frac{2}{N^{tr}}\sum_{\ell \in \small \prod}(\frac{S_{S_{treat}^{tr}}^2(\ell)}{p}+\frac{S_{S_{control}^{tr}}^2(\ell)}{1-p})
\]
其中,\(p\)表示相应treatment组的样本占比,该子式也是最终的计算节点分类标准的公式
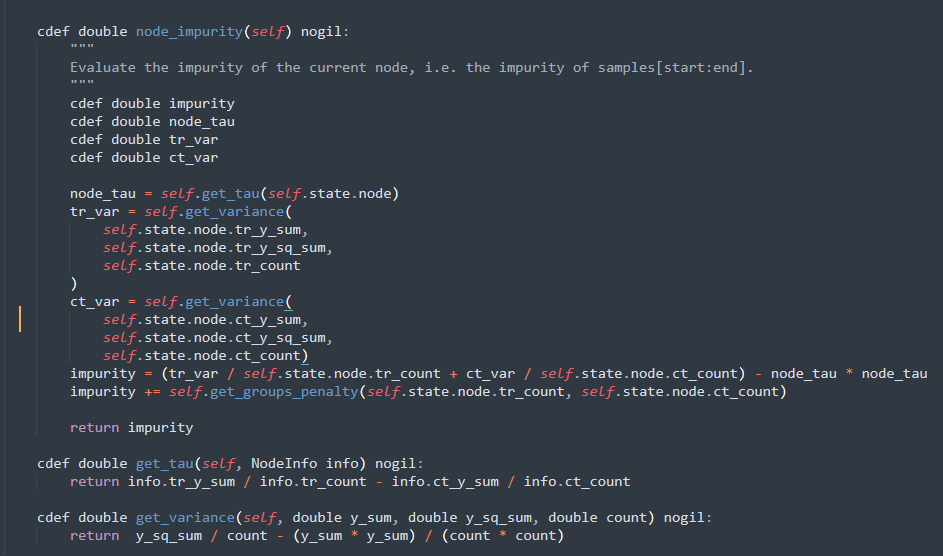
有了节点划分方式之后,build tree的过程和CART树是一样的
推理过程
推理过程和决策树基本一样,树建好之后,只用根据每个node存储的特征和threshold进行path 遍历,走到叶子节点返回值即可。
一般来说,causal tree的叶子节点存储的
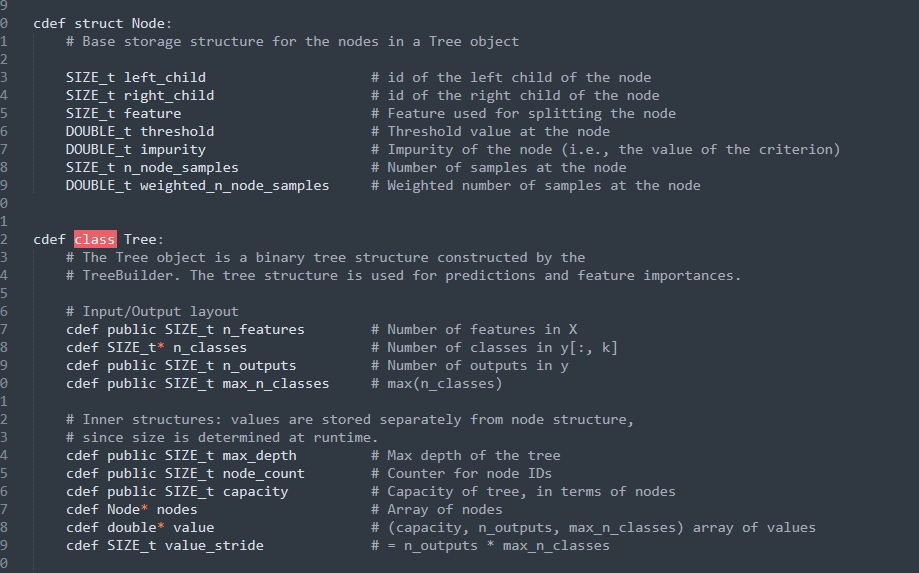
结构体之外还单独存储了一个 叫 value 的数组,主要是存储每个节点的预测值。对于两个Treatment来说,存储的大小就是1x2的list,第一个element存储了control的 正样本比例,第二个element存储了treatment的正样本比例。
一般来说,这个比例会做配平或者说惩罚:
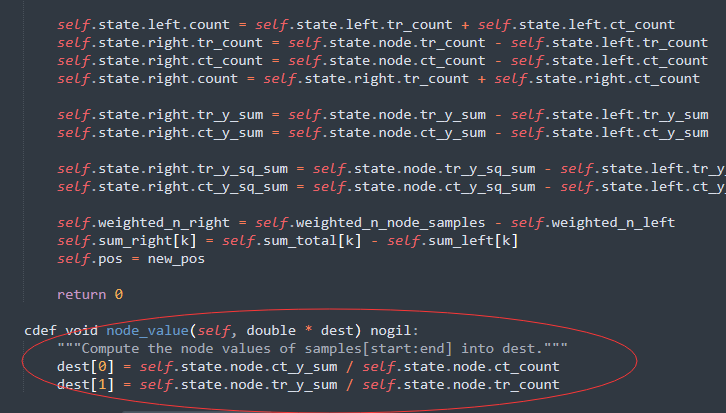
所以,最终推理得到的是一个输入一个样本X,得到T-C的treatment effect,我们不用像meta-learning类的模型一样,自己手动减得到ITE。
Causal Tree总结
- 作者改进了MSE,主动减去了一项模型参数无关的\(E[Y_i^2]\)。改进方法的MSE包含了组内方差,这个方差越大,MSE就会越低,所以它能够在一定程度上限制模型的复杂性
- 把改进的 mse loss apply 到CATE中来指导节点分割 和 建立决策树
- 构建树的过程中,train set切割为了 \(S^{tr}\) 和 \(S^{est}\) 两部分,node的预测值由\(S^{est}\) 进行无偏估计,虽然最后实际上\(S^{est}\) 用train set替代了。
- 理论上causal tree 仅支持 两个Treatment
如果使用causalml的package,如果存在多个T,非C组都会被置为一个T
REF
- https://hwcoder.top/Uplift-1
- 工具: scikit-uplift
- Meta-learners for Estimating Heterogeneous Treatment Effects using Machine Learning
- Athey, Susan, and Guido Imbens. "Recursive partitioning for heterogeneous causal effects." Proceedings of the National Academy of Sciences 113.27 (2016): 7353-7360.
- https://zhuanlan.zhihu.com/p/115223013