全局模型可解释之部分依赖图:Partial Dependence Plot
本部分是来自大纲 模型可解释的一个子分支。
部分依赖图可以表示1个或者2个特征对模型的预测结果所能产生的边际效应。同时也能展示1个特征和label直接是否具有:线性相关性、单调性等。
当我们把pdp应用在线性回归上的时候,通过pdp,我们能够计算每个特征与label之间的线性相关性,其公式表述为
当然pdp也可以适用与分类,只要把输出改成概率就行了,本质上,和回归任务没有太大的区别,对于多分类,可以用 one VS Rest的策略。
其中,\(x_s\)是我们本次关心的1到2个特征,而\(X_C\)则是其他剩余输入模型的特征,\(\hat f\)是本次的模型。通过不断改变\(x_s\)的取值,来看模型预测结果的变化,这时候通过pdp能得到一个特征是怎样影响模型预测的。总结一下:特征重要性展示的是哪些变量对预测的影响最大,而部分依赖图展示的是特征如何影响模型预测的
可以用部分依赖图回答一些与下面这些类似的问题:
- 假如保持其它所有的特征不变,经纬度对房价有什么影响?换句话说,相同大小的房子,在不同的地方价格会有什么差别?
- 在两组不同的人群上,模型预测出的健康水平差异是由他们的负债水平引起的,还是另有原因?
上面,度量特征变化所带来的影响的微分函数也可以表示为模型输出的均值:
具体操作就是:先固定住其他特征,把你感兴趣的这个特征全部批量的改成某个值,不断从某个低值改到某个高值,看所有样本预测结果会做什么变化。
所以说,部分依赖图其实是一种“全局解释模型的方法”
pdp有一个前提假设是,你分析的特征和其余的固定特征没有任何的相关性。如果不能满足这个假设的话,解释的结果可能会存在无法理解的地方。
对于离散值的pdp
对于连续值,我们每次只做微小的改动,对于离散值,这个改动幅度换成“离散特征的取值”就ok。
因为pdp可以同时看一个或者2个特征,所以分两种情况。
1d特征依赖图
我们以泰坦尼克数据集为例子,单独查看'Fair'这个特征,表示乘客登船所需花费的费用。大概可以看到,随着你登船的价格变高,你生还的概率也随之变大。
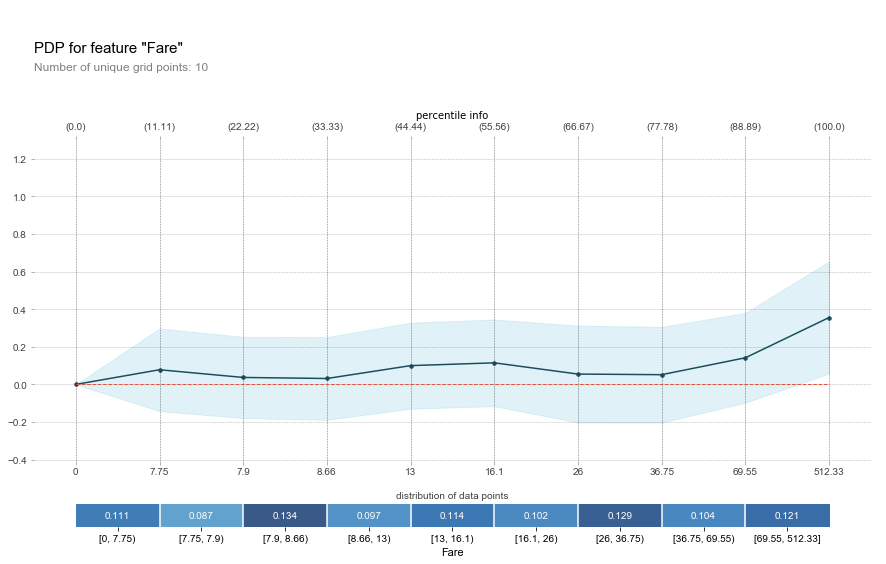
阴影部分表示95%置信度,x轴方块是一些特征的分段,以及每个分段上人数的占比,头部方块是分位数。
2d特征依赖图
除了看一个特征之外,我们也可以同时看年龄和上船费用两个特征在pdp下是如何交互的。
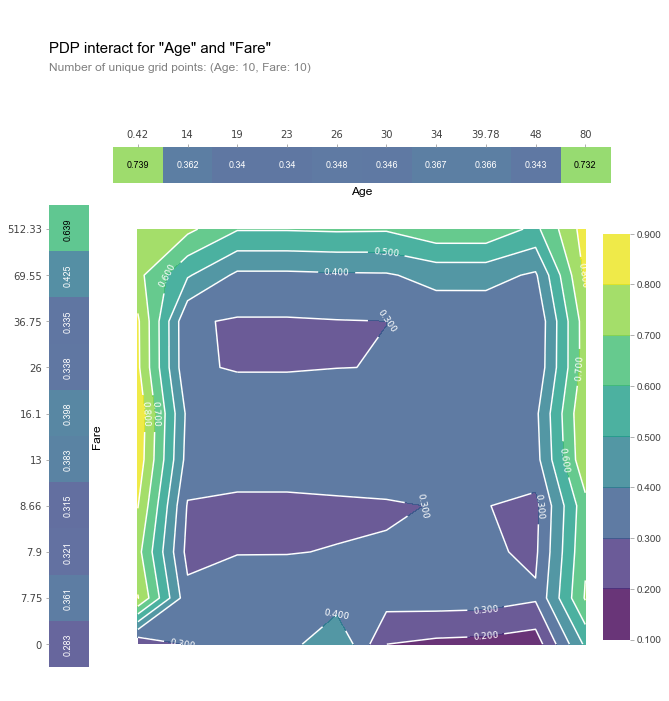
在这上面你可以看到,年龄越大,且上船费用越高的人,他活下来的概率最大。
pdp的有点
- 直观,容易理解
- 可以从因果推理的角度去解释pdp,我们每改变一次特征取值,相当于对pdp进行了一次“treatment”的操作。
pdp的缺点
- 分析特征受限:每次只能分析1个或者2个,不能再多了
- 强假设,如果特征之间具有相关性,则结果往往会出乎你的意料: 比如你有2个特征,身高和体重,以及label:步行的速度。我们想看体重是如何影响步行速度的。那么在pdp的时候,我们相当于在原有的模型学习到的样本空间下,新增了一些样本点,分析结果就有可能得出 在身高2米的时候,体重为30,步行速度xxx,事实上,2米的身高不太可能出现30kg的体重,这很难解释清楚。
- 容易忽略异质条件的影响:举个case,假设你选的这个特征,有一半样本与预测正相关——特征值越大预测越大,—而同时呢,另一半负相关——特征值越小预测越大。这个时候,因为pdp是输出的模型预测值的均值,所以有可能导致这两部分样本相互抵消了,也就是,当你的特征变低的时候,一半样本输出低概率,一半输出高概率,两边加起来求个avg之后,抵消了.....凸(艹皿艹 )
最终你会得出:“这特征没对模型啥用”的结论。这个问题会放在局部模型可解释中的ICE部分再描述怎么解


