SVM三则

硬间隔SVM

SVM被提出来, 解决模式识别中, 数据的分类问题,属于有监督算法中的一种,

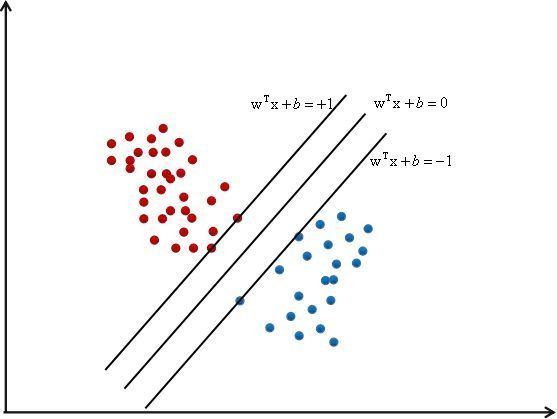
如上图所示, 于其他的线性回归方式不同, SVM企图去寻找一个最完美的超平面, 因为能正确分类样本的线, 它有很多条, 有时候, 像LR一样的模型, 当数据有噪声的时候,很容易越过分类边界, 造成误分类. 而SVM就是确保在分类正确的前提下, 使得数据点与分类之间的间隔最大化,所以, 目的也很明确了, 第一是要寻找这个最大间隔, 也就是这两条边界线到底是多少,其次是保证样本分类正确.
SVM被表示为参数和数据的线性组合,即

\[f(x)=sign(w^Tx+b) \]

其中\(w^Tx+b=0\),就是中间的那条线

最大化间隔

前面我们提到, 要最大化样本点与分界线之间的间隔, 其实就是寻找点到直线的最大距离, 而这些点在哪?有很多的点,就是很多的样本, 起作用的点就是关乎分界线位置的点, 我们定义间隔为1, 那么对于这两条线,我们定义为

\[\begin{cases} w^Tx+b=1, y=1\\ w^Tx+b=-1, y=-1 \end{cases}\]

这里有1个问题
为什么间隔为1?
这个问题,其实1是为了好算吧,当然可以设置成2, 3,...只要成比例的增加\(w,b\)就可以了

这两条线还有另外的功能: 就是让该有的点,尽量的处于自己的那一侧, 转化成数学表达就是

\[\begin{cases} \tag{1} w^Tx+b \geq 1, y=1\\ w^Tx+b \leq 1, y=-1 \end{cases}\]

现在,我们要找到这这个点, 相应的, 就应该有距离的存在, 那么点到直线的距离公式为:

\[r = \frac{|w^x+b|}{||w||} \]

这里\(||w||\)默认为1范数, 其实2范数也是可以的, 我们知道, 关乎分界线命运的点, 在这条分界线上, 因为他们离这两条线的距离最短(如果有的话),这些在这两条线上的点,我们叫做支持向量,因为第一, 这些点其实在高维的时候就是特征向量嘛
显然, 如果在线上,那么\(|w^Tx+b|=1\),于是

\[r=\frac{1}{||w||} \]

那么我们的距离优化就有了:最大化间隔\(\max r\), 但是一般我们将最大化问题转换为最小化问题,以及这样可以转化为二次规划问题,那么最大化\(r\),相当于最小化\(||w||\), 然后把它变成一个二次规划问题:最小化\(||w||^2\)

\[\min r = \min\frac{1}{2} ||w||^2 \]

形成约束问题

第一是优化\(r\),其次是优化分类的正确性
对于(1)式, 根据同号原则,其可以被表达为

\[\begin{cases} \tag{2} y(w^Tx+b) \geq 1, y=1\\ y(w^Tx+b) \leq 1, y=-1 \end{cases}\]

我们希望尽可能正确的分类,所以约束优化问题的集合就是

\[\begin{cases} \tag{3} \min \frac{1}{2}||w||^2 \\ \min y(w^Tx+b)\geq 1 \\ \min1-y(w^Tx+b) \geq 0 \end{cases} \]

拉格朗日乘子变换

一般,我们将带约束的优化问题都转化为拉格朗日乘子法经行计算, 这样可以将整个带约束的优化集合转化为一个函数式子
拉格朗日乘子法请看
https://blog.csdn.net/u014792304/article/details/78396955?utm_source=distribute.pc_relevant.none-task

转换后的式子为:

\[L(w,b,x)=\frac{1}{2} ||w||^2+\sum_{i=1}^{N}\lambda_i (1-y(w^Tx+b)) \]

其中, \(\lambda \geq0\)为拉格朗日乘子

KKT条件

我们知道, 拉格朗日乘子法可以表示为:

\[L(x,\lambda)=f(x)+\lambda g(x) \]

但是我们本质上优化的还是不等式约束, 不等式约束需要满足KKT条件

\[\begin{cases} g(x) \leq 0 \\ \lambda \geq 0 \\ \lambda g(x)= 0 \end{cases}\]

于是, 我们的式子, 满足KKT条件,需要为:

\[\begin{cases} (1-y(w^Tx+b)) \leq 0 \\ \lambda \geq 0 \\ \lambda_i(1-y(w^Tx+b)) = 0 \end{cases} \]

为什么引入KKT条件?

• KKT条件是对最优解的约束，而原始问题中的约束条件是对可行解的约束。

对偶问题

对偶是吧原来的式子 min max L 转化为 max min L, 一来是它们近似, 二是这样可以先求解w,b, 然后只用管\(\lambda\),而\(\lambda\)只在支持向量上有作用 问题求解简单化 我将其转化为原问题的对偶问题, 转化为对偶问题之后, 全局上就变成了一个最小化的问题, 我们的原问题是

\[\min \limits_{w,b} \max \limits_{\lambda} L(w,b,x) \]

那么它的对偶问题就是

\[\max \limits_{\lambda} \min \limits_{w,b} L(w,b,x) \]

我们将问题的函数表达视作凸二次规划问题,这样可以分别对参数求偏导求解

\[\min \max L \geq \max \min L \]

这样的关系,我们称其为弱对偶关系,强对偶就是 相等
我们对无约束问题求偏导, 此时\(\lambda\) 看做常量

\[\frac{\partial L}{\partial b} =0=-\sum_{i=1}^{N} \lambda_i y_i \\ \]

将其带入\(L\)

\[L(w,b,\lambda) = \frac{1}{2}||w||^2+\sum_{i=1}^{N} \lambda_i-\sum_{i=1}^{N} \lambda_i y_i(w^Tx_i+b) \\ =\frac{1}{2}||w||^2+\sum_{i=1}^{N} \lambda_i-\sum \lambda_i y_iw^Tx_i-\sum \lambda_i y_ib\\ =\frac{1}{2}||w||^2+\sum_{i=1}^{N} \lambda_i-\sum \lambda_i y_iw^Tx_i \]

接下来对\(\lambda\):

\[\frac{\partial L}{\partial w}=||w||-\sum \lambda y x \\ w=\sum \lambda y x \]

再次带入\(L\)并化简:

\[\max \limits_{\lambda} \sum \lambda-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N} \lambda_i \lambda_j y_i y_j x_i^T x_ j \]

那么\(b\)呢? 我们通过KKT条件来解\(b\)
我们把

\[\lambda_i (1-y_i(w^T x_i+b)) =0 \]

称作作松弛互补条件
并设置2条虚线, 有点落在线上时, 就是松弛条件的解
我们假设存在\((x_k,y_k)\)

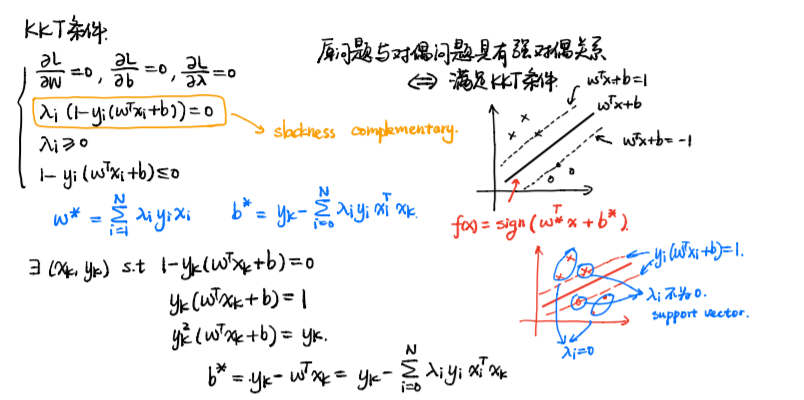
那么. 最后, hard-margin的解为:

\[f(x)=sign(w^Tx+b) \]

\(w\)可以看作是数据\(x\)的线性组合, 但对于\(\lambda\) ,当且仅当数据落在两条虚线上时, \(\lambda\)才有值,对于其他的sample, \(\lambda\)不起作用,这部分叫支持向量

引入 SMO

软间隔SVM, 松弛变量\(\xi\), 和惩罚系数\(C\)

思想: 允许存在一点点错误

• hard-margin:假设数据是非常理想的, 数据是可分的
• soft-margin:数据是含有噪声的, 或者难以分类的
  公式:在原先的基础上, 加上一个损失

\[\min\frac{1}{2}||w||^2+loss \\ \min\frac{1}{2}||w||^2+C\sum_{i=1}^{N} \xi_i \]

这里的损失可以理解为:距离,(hinge loss,合页损失)

\[\begin{cases} if\quad y_i(w^Tx+b) \geq 1, lss = 0 \\ if\quad y_i(w^Tx+b) \leq 1, loss = 1-y_i(w^Tx+b) \end{cases}\]

\(\xi\)和\(C\)的问题

首先, 软间隔SVM通过增加一个合页损失, 来增加SVM的容忍度, 我们将错分时候的损失表示为

\[1-y(w^Tx+b) \]

并将其记为\(\xi\), 仔细看来, 这个\(\xi\)的作用是:
表示样本偏离离群点或者偏离分界线的一个程度,当然,肯定是往错误的方向偏
而对于\(C\)来说, 其可以理解为一个惩罚项, 表示着模型对错分样本的容忍度, 惩罚因子C决定了你有多重视离群点带来的损失，显然当所有离群点的松弛变量的和一定时，你定的C越大，对目标函数的损失也越大，此时就暗示着你非常不愿意放弃这些离群点， 最极端的情况是你把C定为无限大，这样只要稍有一个点离群，目标函数的值马上变成无限大，马上让问题变成无解，这就退化成了硬间隔问题

核SVM

其实核函数是将低纬空间的点, 转化到高维空间中去, 让线性不可分变得可分, 核函数内, 大部分是向量内积的一个操作

优化公式:

\[\max \limits_{\lambda} \sum \lambda-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N} \lambda_i \lambda_j y_i y_j kernel(x_i, x_ j) \]

其实, 就是对\(x_i, x_j\)进行一种变换: 常见的核如:

• 线性变换: \(x^Tx\), 可以分离出一个平面

各种核函数
https://blog.csdn.net/yefcion/article/details/81099390?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.compare&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2.compare