逻辑回归LR

逻辑回归是什么

逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法，运用梯度下降来求解模型的参数，并通过sigmoid激活, 输出一个0~1的概率值, 来达到将数据二分类的目的。

公式&理解

下面我们开始LR的公式推理
LR的表达式如下

\[f(x)=\sigma(w^Tx+b) \]

其中, \(\sigma=sigmoid=\frac{1}{1+e^{wx+b}}\)
LR假设数据服从二项分布，也是事件非0即1，那么我们的样本在特征\(x\)下被取到0和1的概率就可以被表示为

\[ P(y|x)=\left\{ \begin{aligned} & p, y=1 \\ & 1-p , y=0 \\ \end{aligned} \right. \]

稍微化简一下这个表达式就是

\[P(y|x)=p^{y}(1-p)^{1-y} \]

那么这是当我们只有一个样本的时候情况情况，多条样本的时候，根据极大似然法则我，求多次实验下样本在参数w下使得样本被取得1得概率最大：

\[P=P(y_1|x_1)P(y_2|x_2)...P(y_n|x_n)=\prod_{i=1}^{N}p(y_i|x_i) \]

理想情况下，我们希望找到使P(y|x)最大化的参数w。但是实际上，为了简单起见，通常不直接使用这个函数，而是使用其负数对数。一方面，计算机更适合做加法，还有另一个更重要的原因是：因为对数是一个严格单调的函数，最小化负对数似然将得到直接最大化似然函数时的参数\(w\)

\[\begin{align*} \ln(P) &=\sum_{i=1}^{N}ln(p(y_i|x_i))\\ &=\sum_{i=1}^{N}\ln(p^{y}(1-p)^{1-y})\\ &=\sum_{i=1}^{N}\big[y\ln p+(1-y)\ln (1-p)\big] \end{align*} \]

其中，\(P=sigmoid(x)=\frac{1}{1+e^{-wx}}\)，我们把公式定义为：

\[L(w)=\sum_{i=1}^{N}\big[y\ln p+(1-y)\ln (1-p)\big] \]

\(L(w)\)就是逻辑回归得损失函数，也叫对数似然损失，这是一个样本得时候，可以发现这个损失就是二分类交叉熵损失得形式。而交叉熵又属于KL散度的一部分，KL散度是一个 熵+交叉熵的形式，不过因为熵的部分只和真实的样本分布有关，所以一般求梯度的时候就是0，所谓忽略掉熵，留下的就是交叉熵。主要的功能就是取衡量2个分布就是：真实的分布和预测分布之间的一个距离。KL散度也有一个缺点就是它是不对称的，既然是距离，那就是说AB个分布之间的关系是A到B的距离应该等于B到A的距离，但KL散度不具备这种性质，所以在它的基础之上又出现了JS散度，著名的GAN的度量的其实就是JS散度。上面是一堆废话了，接下来看看如何求解参数\(w\)。参数的求解方式是强大的梯度下降策略，说白了就是求偏导，因为函数(这里就是损失)下降最快的方向就是梯度的方向。

\[\begin{align*} \frac{\partial L(w)}{\partial w} &= \sum_{i=1}^{N}\big[y{\ln p}^{'}+(1-y){\ln (1-p)}^{'}\big] \\ &=\sum_{i=1}^{N}\big[y\frac{1}{p}{p}^{'}+(1-y)\frac{1}{1-p}{(1-p)}^{'}\big] \\ &=\sum_{i=1}^{N}\big[y\frac{1}{p}p(1-p)x-(1-y)\frac{1}{1-p}p(1-p)x\big] \\ &=\sum_{i=1}^{N}\big[y(1-p)x-(1-y)px\big] \\ &=\sum_{i=1}^{N}\big[(y-p)x\big] \end{align*} \]

值得注意的是 \(\frac{\partial p}{\partial w}=p(1-p)x\), \({(1-p)}^{'}=-p(1-p)x\)
所以，最终我们的表达式就是：

\[\nabla L(w)=\sum_{i=1}^{N}(y_i-p_i)x_i=\sum_{i=1}^{N}(y_i-\frac{1}{1+e^{-w^Tx_i}})x_i \]

\[w_{t+1} = w_t+\eta \nabla L(w) \]

到此为止，使用梯度下降更新参数的过程就结束了。

加深理解

为什么LR不使用平方损失，而使用对数似然损失？

这个涉及到梯度下降过程中的loss求导的时候，我们看如果使用交叉熵的话，求导之后的loss是这样的：

\[\nabla L(w)= \sum(y-p)x=\sum(y-\sigma(z))x \]

其中 \(p=\sigma(z)\)表示，\(z\)是关于x的函数，就是sigmoid。
如果loss换成mse的话，那么loss就是

\[L(w)=\frac{1}{N}\sum_{i=1}^{N}(y_i-p)^2 \]

求导之后就是:

\[\nabla L(w)=\frac{1}{2N}\sum(y-p)p^{'} \]

知道\(p\)就是sigmoid，那么对sigmoid求导之后，因为sigmoid导数最大值是0.25，会使得求得的梯度很小，损失函数收敛的很慢。可以看sigmoid和它的导数的图像

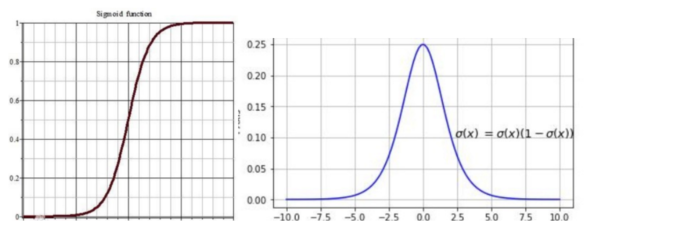
为什么是sigmoid做激活？

严格来说，之所以用sigmoid是推导出来的。

提LR就不可不谈的问题之：正则化、并行化、重复特征的处理

• L1正则，生成稀向量
• L2正则，减小权重
  https://www.cnblogs.com/zhouyc/p/12505093.html

LR适合那些类型的数据，为什么？

LR理论上来说，比较适合高维离散的数据。

• 一方面，LR做为一种线性模型，其本身求解速度快的特点相对于一些更复杂的树模型来说比较有优势
• 另一方面，高维离散的条件下，一般来说大维度下样本很大可能是线性可分的，所以也不需要太复杂的模型，也就是说，带上正则后的线性模型与树模型相比，比较不容易产生过拟合

LR做多分类：类间互斥&类间不互斥

类间互斥：加softmax，分类逻辑回归不是用的二分类交叉熵嘛， 可以考虑换成多分类的交叉熵损失，前提是套上一层softmax，这样lr就变成了softmax回归
类间不互斥：为每个类别训练一个lr，然后预测的时候，这些样本都过每一个lr模型，看谁的概率大