因果推断review

什么是因果推断？

因果推断(Causal Inference)：就是预估对某个对象/群体/人 等 做不做某种干预后产生的结果。

常说‘关系不代表因果’. 比如，一项研究表面，吃早餐的女孩比不吃早餐的女孩更瘦，因此得出结论：‘吃早餐能减肥‘。 但事实上，吃早餐和瘦这2件事也许只是存在相关性，瘦并不是吃早餐的 果，也就是它们并不存在因果关系；事实上，也许吃早餐的女孩瘦是因为她有很多好的生活习惯比如：起得早，睡得早，健身等，最终使他变瘦。我们把’吃早餐和瘦‘ 之间的其他能够影响结论的变量称之为 混淆变量(coudounding variables), 如健身。

做因果推断最行之有效的方法是做随机对照实验(randomized controlled trials, rct).也就是 A/B test. 然而很多时候，做rct需要费时费力，而且有时候，随机对照实验是受限制的，不一定在任何情况下都可以做随机对照实验。如有时候，会收到道德问题的约束：观测数据通常是由研究者简单的观察每个样本收集得到的，收集期间，不对其做任何的干预，从观测到的数据中能获取样本的行为。对已经观测得到的数据，还有一个核心的问题是我们拿不到 ‘反事实’(counterfactual outcomes), 比如说 “对某个病人，他已经注射了100ml的药物，没有产生副作用(事实 factual outcomes)， 但我们想知道如果他注射200ml会怎么样(反事实)“，这样做其一是不道德的，其二是他已经被注射了100ml，再注射就不是随机对照了，已经破坏了控制变量的条件。rct的另一个缺点是关注的是样本的平均层面，但忽略了每个独立的样本本身的特点。

为了解决因果推断领域的这些个问题，一共产生了2套框架，分别是

• potential outcome framework()潜在结果架构) , 通常也叫做 Neyman-Rubin Potential Outcomes 或者 the Rubin Causal Model, RCM)
• structural causal model(SCM)

在上面提到的例子中，为了去评估吃早餐对女孩所带来的因果效应，我们必须拿到同一个人在同种情况下的不同结果，也就是这个人，吃早餐/不吃早餐所带来的体重变化。显然，在同一时间段内，同时看到这两种结果(potential outcomes)时不可能的，不管怎么做，始终都会存在其中一个结果的缺失。而RCM就是去做这件事情的。RCM的目标时预估潜在结果，从而计算干预效果(treatment effect).

另一种模型就是SCM，因果推理中的另一个有影响力的框架是结构因果模型（SCM），其中包括因果图和结构方程式。结构因果模型描述了系统的因果机制，其中一组变量和它们之间的因果关系由一组联立结构方程式建模。

因果推断和机器学习有着千丝万缕的关系，从某种程度上说，机器学习促进了因果推断在潜在结果预估方面的成效，同时，因果推断有帮助如推荐系统等算法更好的决策。目前，潜在结果模型有三个假设，其他的所有因果推理的方法，基本上都是在这三个假设下进行的。
目前有如下的一些方法

• re-weighting
• stratification
• matching-based
• tree-based
• representation-based
• muti-task
• meta-learning

因果推断基础

总的来算，因果推断所做的任务就是当treatment改变的时候，去预估这个改变所带来的结果，比如说：对于同一批人，我一开始并未给他推荐某个产品，他没有购买，但如果给他推荐的话，他会不会购买？这里的推荐/不推荐就是treatment，会不会购买就是potential outcome。再例如，假设可以对患者使用两种治疗方法：药物A和药物B。将药物A应用于感患者时，恢复率为70％，而将药物B应用于相同患者时，恢复率为90％，恢复率就是潜在结果，恢复率的变化是treatment effect。但是上述的实验，基本上只能通过近似的随机对照实验来获取结果，但rct非常的消耗资源，因此从已观测到的数据进行treatment effect预估变得很有价值。
通常来说，观测数据包含接受到不同treatment的对象，以及treatment下不同的结果，这些结果可能还有更多的信息，这样的观察数据使研究人员能够研究根本的问题，而无需进行随机实验即可了解某种治疗的因果效应

名词定义

causal inference：因果推理/因果推断
causal effect 因果效应
treatment: 干预/治疗; 其实就是做不做A动作的意思。比如智能营销下，发券还是不发券，还是发什么券。

• \(W\)表示reatment，\(W\in \{0,1,2...n\}\)， 通常在大部分情况下，treatment是二值化的，即要么treat要么不treat，非0即1

potential outcome: 潜在结果，\(Y=(W=w)\)

• factual outcom:
  • \(Y^F=(W=w)\) ，事实结果，已经做了某个treatment并观测到的结果
• counterfactual outcome
  • \(Y^{CF}=(W=w^{'})\), 反事实结果，如果这个对象做了这个treatment，他的结果会是怎么样的？当treatment是二值化的时候，\(Y^{CF}=Y(W=1-w)\)

treatment effect：治疗效果
治疗效果可以从三个层面去衡量：全集，子集和个体。同时针对不同的层面，会有不同的计算effect的方式，有ATE,CATE,ITE等
unit：单个的实验对象，可以是一个人，一个物体，一个对象
pre-treatment varialble/post-treatment varialble:干预前变量

• coufounding variable：混淆变量，对治疗和结果都有影响的变量

randomized controlled trials: RCT随机对照实验

三个重要的假设

假设1：Stable Unit Treatment Value Assumption(SUTVA)
这个假设强调两点：

• 每个单元的独立性，即单元之间没有交互作用。在上面的示例中，一个患者的结果不会影响其他患者的结果
• 每种治疗的单一性，在上面的示例中，在SUTVA假设下，具有不同剂量的药物A是不同的治疗方法。

假设2：Ignorability
在给定的条件下(可以理解为对象的特征) treatment与潜在结果相独立

\[W \perp \!\!\! \perp (Y(w=0), Y(W=1)|X) \]

该假设同样包含2点

• 如果两名患者具有相同的条件变量X，则无论治疗方案如何，其潜在结果均应相同
• 如果两名患者具有相同的条件变量X，则他们的治疗分配机制都应该相同
  假设3：Positivity
  对于任何条件X，干预方案都是不确定的,也就是说，无论做什么treatment，在任何时候，只有一个outcome

\[P(W=w|X=x)>0 \]

这个条件对于 treatment effect预估是非常重要的。

常用计算公式

此处以二值化的treatment作为例子

ATE：average treatment effect

在全集层面(population level), 干预效果被称为 Average Treatmen Effect(ATE)

\[ATE=E[Y(W=1)-Y(W=0)] \]

其中，\(Y=(W=1)\) 表示实验组的结果，\(Y=(W=0)\) 表示对照组的结果。表现上就是群体性treat的effect取平均，含义上等于对一群人做了干预 - 不做 干预产生的效果值。比如 发券-不发券 后的增益。

ATT：Average Treatment effect on the Treated grou

\[ATT=E[Y(W=1)|W=1]-E[Y(W=0|W=1)] \]

CATE: Conditional Average Treatment Effect

条件平均治疗效应，意为在不同条件下取treatment，所产生的效果，它又被称作heterogeneous treatment effect。这个不同的条件可能产生的是不同的sub group，入上表中年龄产生了3个sub group

\[CATE=EY(W=1)|X=x]-E[Y(W=0)|X=x)] \]

ITE：Individual Treatment Effect

在个人层面上的treatment effect评价

\[ITE_i=Y_i(W=1)-Y_i(W=0) \]

做一个汇总

混淆变量、辛普森悖论和常用的处理手段

混淆变量(confounders) 会影响treatment和outcome之间的因果关系，从而影响到treatment effect的预估。coufounder是一种特殊的干预前变量，比如药物治疗中的年龄，老龄人的体制和年轻人是不一样的，因此，同一种药物也许会出现不同的反映。当计算ATE的时候，混淆变量所产生的效果也会被计算在内，这导致了一种虚假效应(虚假效应). 使得我们得到错误的结论

辛普森悖论(Simpson's Paradox)：某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。平时大小考试都很牛b，一到大考就GG。

比如上方表格中，比如这个表，恢复率作为ATE，一定能说明 A效果比B好吗？threatment b在各年龄段上效果其实比threatment a要好，但当汇总来看的时候，得到的确实截然相反的结果。分层下的好坏不能决定最终结果的好坏。

辛普森悖论，很大程度上是由于混淆变量带来的，比如年龄。

选择偏差

那么什么带来的了混淆变量呢？是选择性偏差。简单的来说，选择偏倚就是观测到的数据，其分布和我们感兴趣的目标的分布不一样。

混淆变量导致了选择偏倚的产生，从而加大了反事实的偏差，进而会影响到ATE的预估。
从上一个表中和下图中看出，不同的年龄分布，导致相同的treat产生了不同的outcomes分布

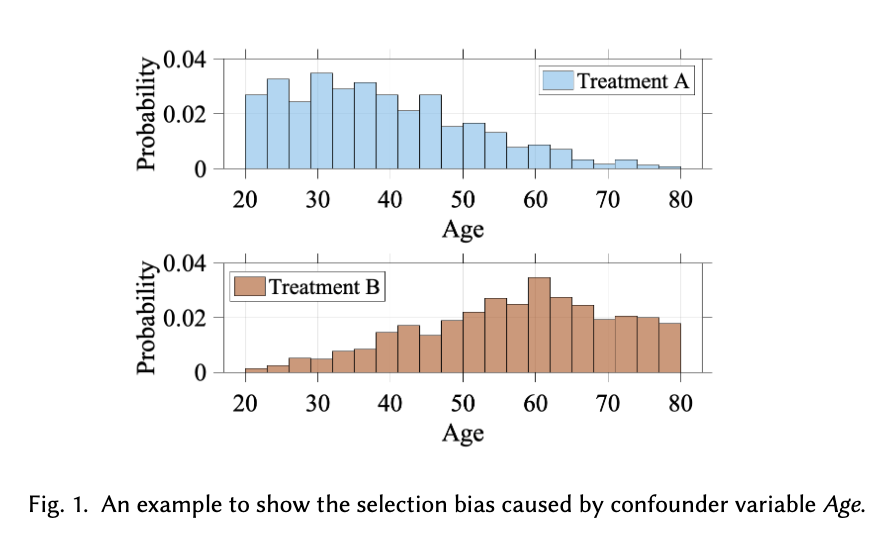
如果我们直接开始在观测数据上建模，即$$\tilde Y=f_w(x)$$, 那么显然模型因为选择性偏倚的存在，会表现的很糟糕。为了解决选择性偏倚的问题，通常有2种做法

• 造一个与目标分布差不多的伪集合，可以用的算法有sample re-weighting，matching，tree-based，muti-task。这个方法能够减轻coufounder带来的影响，也使得模型能够更好的预估到 反事实。
• 另一方法是先在观测数据上训练一个基础模型，然后再纠正选择性偏倚，meta-learning就属于这个方法

三个假设条件下的因果推断模型

大部分的因果推断模型都依赖上面提到的3个假设，根据他们对coufounder的处理方式的不同，这些方法可以被分为这么几个类别：

• Re-weighting methods
• Stratification methods
• Matching methods
• Tree-based methods
• Representation based methods
• Multi-task methods
• Meta-learning methods