机器学习常见评价指标与优缺点
先引入一个经典的表,辅助我们, 这个表叫做混淆矩阵
准确率(Accuracy)
准确率反映了模型模型做出正确预测的比例
计算公式
准确率假设不同的分类是同等地位的，例如对猫狗洗好进行分类，问题中并没有对猫和狗有特定的侧重，因此在这里我们只强调于分类的正确度，即准确率。
优点
- 计算简单, 时间复杂度低
缺点
- 当正负样本比例不均衡的时候, 准确率就抓瞎了, 比如我样本里面有99个负例, 1个正例, 那模型预测的时候, 把100个样本都当中负例, 我的准去率是99%, 这样没什么意思啊
精确率(Precision)
精确率看重的是: 模型做出预测为正类的预测中, 有多少是真正的正类
举个例子: 警察抓小偷, 警察抓小偷，描述警察抓的人中有多少个是小偷
召回率(Recall)
召回率又可以被翻译为查全率，同样基于对于正(Positive)案例的指标。但与精确率不同之处在于，召回率更加侧重真实为正(Positive)的样本中被成功预测的比例。
举个例子, 也是警察抓小偷, recall反映的是: 描述有多少比例的小偷给警察抓了
它们的缺点
精确率或者召回率作为度量标准其实存在一个很大的问题，一批样本, 比如单独用precisoion的话, 我全部预测为正就好了嘛, 肯定能够预测对一个. 又比如召回率, 我多增加一些样本, 比如警察多抓些人, 那肯定抓到小偷的概率就增加了
F1-score
F1 综合了precision和recall的特点, 对它们做了一个调和
举例: 警察抓小偷, 抓到又多又准
ROC
以上的算法都是在做出了分类的情况下,这种情况叫做硬分类,但是很多算法, 都是给出一个概率值, 我们根据一个阈值来对类别做出评价
ROC全称是“受试者工作特征”(Receiver OperatingCharacteristic)曲线。我们根据学习器的预测结果，把阈值从0变到最大，即刚开始是把每个样本作为正例进行预测，随着阈值的增大，学习器预测正样例数越来越少，直到最后没有一个样本是正样例。在这一过程中，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了“ROC曲线”。
ROC纵轴是真正例率(TP rate), 横轴是假正例率(FP rate)
roc曲线通过不断修改预测的阈值,
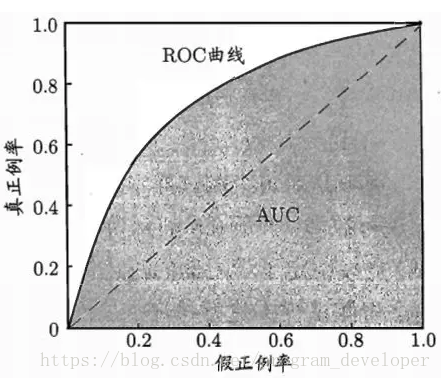
ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类别不平衡（Class Imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化，ROC以及AUC可以很好的消除样本类别不平衡对指标结果产生的影响。另一个原因是，ROC和是一种不依赖于阈值（Threshold）的评价指标，在输出为概率分布的分类模型中，如果仅使用准确率、精确率、召回率作为评价指标进行模型对比时，都必须时基于某一个给定阈值的，对于不同的阈值，各模型的Metrics结果也会有所不同，这样就很难得出一个很置信的结果。
AUC
auc计算方式
https://blog.csdn.net/renzhentinghai/article/details/81095857
AUC就是ROC曲线下的面积
AUC是指随机给定一个正样本和一个负样本，分类器输出该正样本为正的那个概率值比分类器输出该负样本为正的那个概率值要大的可能性。所以AUC反应的是分类器对样本的排序能力。**根据这个解释，如果我们完全随机的对样本分类，那么AUC应该接近0.5。（所以一般训练出的模型，AUC>0.5,如果AUC=0.5，这个分类器等于没有效果，效果与完全随机一样，如果AUC<0.5，则可能是标签标注错误等情况造成）；
另外值得注意的是，AUC的计算方法同时考虑了学习器对于正例和负例的分类能力，在样本不平衡的情况下，依然能够对分类器做出合理的评价。AUC对样本类别是否均衡并不敏感，这也是不均衡样本通常用AUC评价学习器性能的一个原因。
缺点
- roc,auc都只适合于二分类
- AUC只关注正负样本之间的排序，并不关心正样本内部，或者负样本内部的排序。这也体现了AUC的本质：任意个正样本的概率都大于负样本的概率的能力。
- 线上的排序发生在一个用户的session下，而线下计算全集AUC，即把user1点击的正样本排序高于user2未点击的负样本是没有实际意义的，但线下auc计算的时候考虑了它。
优点
- ROC曲线能很容易的查出任意阈值对学习器的泛化性能影响
有助于选择最佳的阈值。ROC曲线越靠近左上角，模型的查全率就越高。最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值，其假正例和假反例总数最少。 - 克服样本不平衡
多分类
- Macro(宏平均): 分别计算每个类的precsion和recall, 再统一平均
- Micro(微平均): 先计算总体的TP FP的数量, 对它们平均之后再计算Precision Recall
