L1 L2正则化

范数

0范数

\(L_0\)范数表示为向量中非0元素的个数

\[L_0-||x||_0 = x_i, (x_i \not= 0) \]

1范数

向量中元素绝对值的和,也就是\(x\)与0之间的曼哈顿距离

\[L_1 = \sum |x_i| \]

2范数

\(x\)与0之间的欧式范数, 也就是向量中的每个数的平方之和

\[L_2 = \sqrt \sum x_i^2 \]

p范数

\[L_p = \sqrt[p] \sum x_i^p \]

正则化的来源

正则化主要是用来控制模型的复杂度, 从而控制过拟合
做法:一般在损失函数中加入惩罚项

\[L(w,x,y)+\alpha \Omega(w) \]

\(w\)显然, 是参数, \(\alpha\)控制正则化的强弱, 是一个常数
从下图讲解:

• 准确率: 右>左
• 模型复杂度: 右>左
  

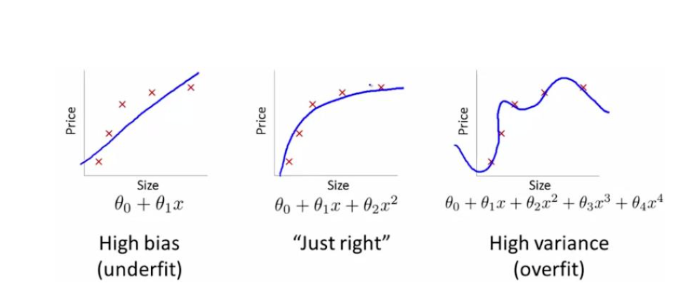
但是在测试的时候, 会出现过拟合的模型, 泛化效果变差的现象

为什么\(L_1\)和\(L_2\)能减小过拟合?

ML的目的是获得做好的参数\(w\), 并让模型的泛化能力更好
当模型复杂的时候, 相应的\(w\)也变多, 于是产生可过拟合现象, 为了降低模型的复杂度, 可以考虑适当的减少参数,代价就是准确率会适当的下降
如何减小参数?: 让\(w\)中的部分元素为0,也就是限制\(w\)中非0元素的个数
那么非0个数如何表示--> \(L_0\)范数, 于是我们有优化问题:

\[\begin{cases} \min L(w,x,y) \\ ||w||_0 \leq C \end{cases} \]

最小化损失, 并且约束是 非0元素的个数, 小于一定的值, 但是这个约束, 不好优化
于是有了\(L_1,L_2\)
初衷是限制w元素0的个数, 但可不可以这样?: 让\(w\)中的某些元素, 尽可能的趋近于0
\(||w|| \leq C\) 或者 \(||w||_2 \leq C\)
那么就可以发现, 刚好, 这是1 2 范数
那么可以得到优化问题

\[\begin{cases} \min L(w,x,y) \\ ||w||_1 \leq C \end{cases} \begin{cases} \min L(w,x,y) \\ ||w||_{2}\leq C \end{cases} \]

然后开始解优化问题, 一般具有约束的优化问题, 可以用拉格朗日函数

\[L(w,\alpha) = L(w,x,y)+\alpha(||w||_1-C) \\ L(w,\alpha) = L(w,x,y)+\alpha(||w||_2-C) \\ \]

上式也可写成

\[L(w,\alpha) = L(w,x,y)+\alpha ||w||_1 -\alpha C \\ L(w,\alpha) = L(w,x,y)+\alpha ||w||_2- \alpha C \]

然后按没有正则化时的计算方式一样, 求偏导,令其为0,求\(w\)就可以了, 这样的化, 和\(\alpha C\)就没有关系了

树形结合

我们继续看对\(w\)的约束项

\(L_1\) 正则

\[||w||_1 \leq C \]

从2维平面的角度来看, \(L_1\)为:

\[|w_1| + |w_2| \leq C \]

从数学的角度, 相当于时是一个菱形

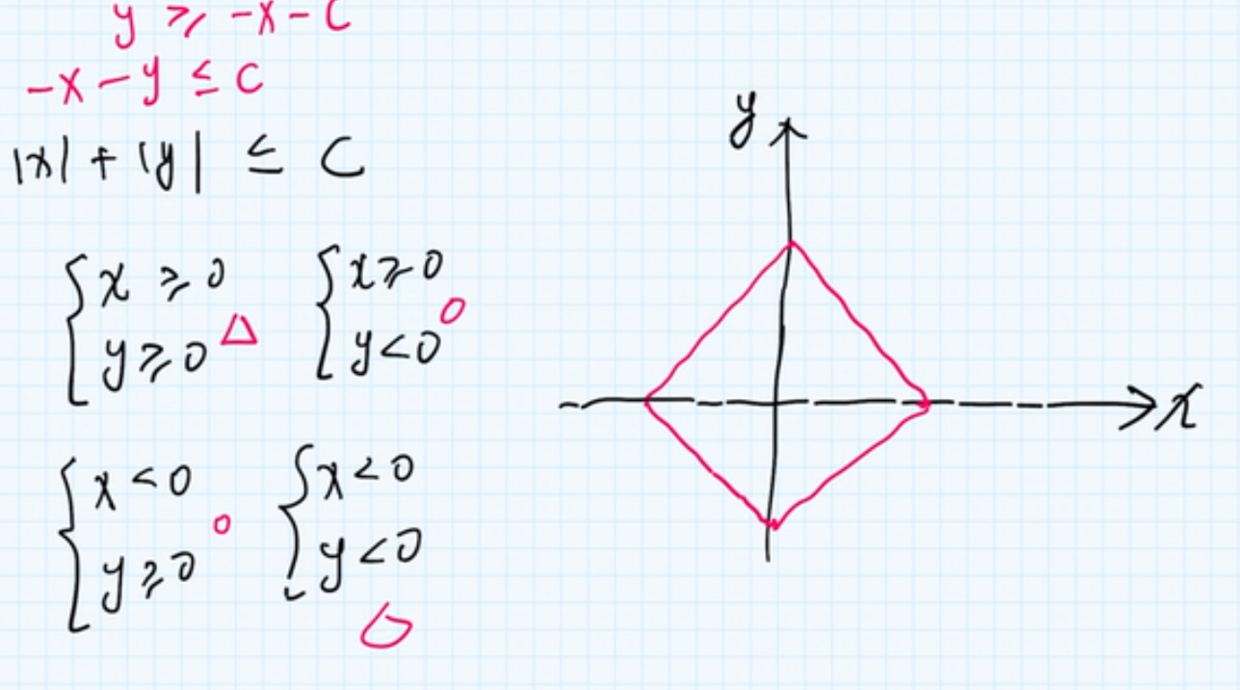
回到问题上, 损失函数是一个等高线图:
那么. 带惩罚项的损失函数的解, 就是 正则项与损失的交点

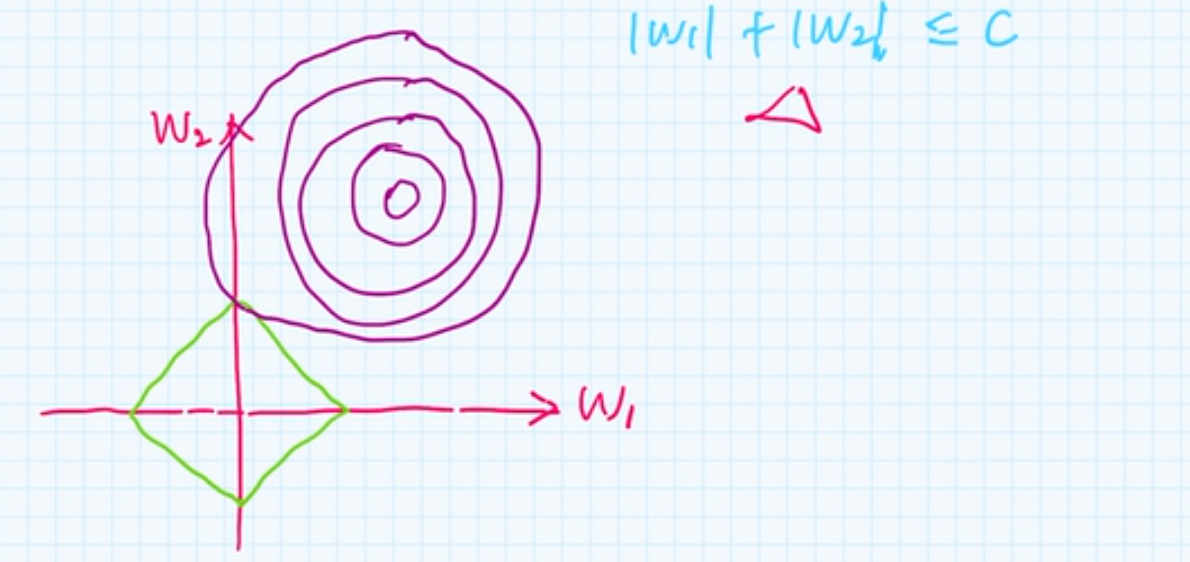
我们可以看到, 交点位置, \(w_1\)为0, 所以也得出一个结论
\(L_1\)正则可以产生稀疏向量,也就是,然某些权重元素为0, 在高维的时候, 交点越多, 也就越稀疏

\(L_2\)正则

\[||w||_2 = \sqrt{w_1^2+w_2^2} \leq C \]

本质上,这是半径为\(C\)的圆的公式

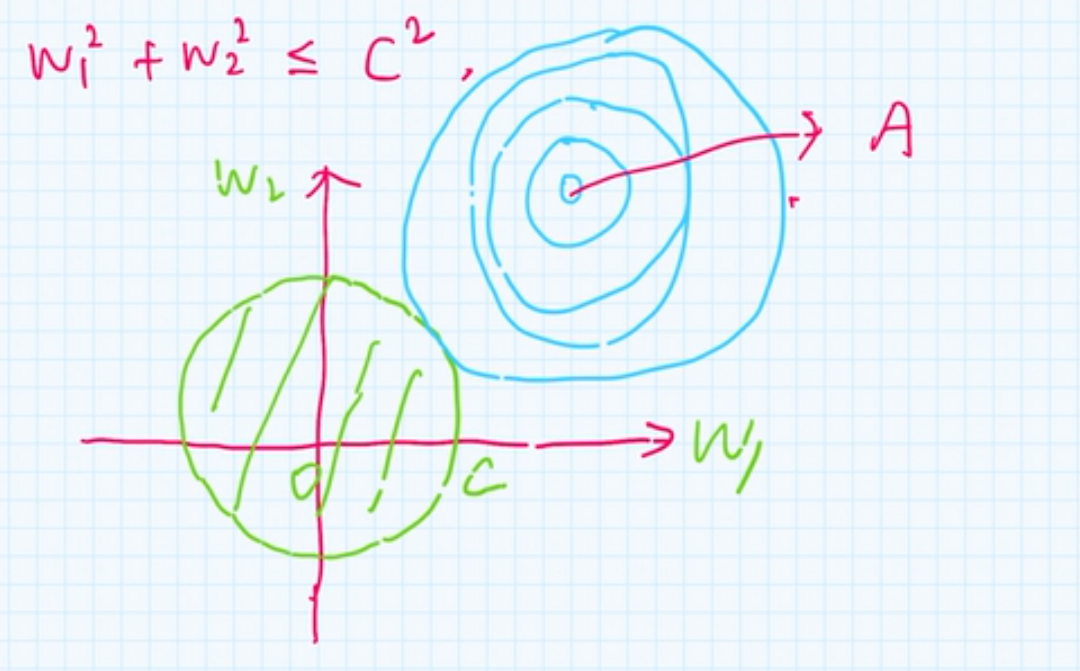
同样最优解在交点处, 且\(w_1,w_2\)不容易为0

L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的规则项||W||2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的哦。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。

L1不可导如何解决?

1. 为什么不可导?

不可导得条件是:

1. 函数在该点不连续
2. 即使连续,函数的左右导数不等
   L1表示: y=|x|, 虽然连续,但是在0的位置, 左导数=-1 右导数等于1,不可导

2. 如何解决?

• 使用坐标下降法
  坐标轴下降法和梯度下降法具有同样的思想，都是沿着某个方向不断迭代，但是梯度下降法是沿着当前点的负梯度方向进行参数更新，而坐标轴下降法是沿着坐标轴的方向。
  先初始化参数, 然后每一轮迭代, 选择一个参数经行优化, 其他参数保持固定
  https://blog.csdn.net/xiaocong1990/article/details/83039802

• Proximal Algorithms 近端梯度下降
  

L1&L2一起作用也是可以的