20172308 《程序设计与数据结构》第八周学习总结

教材学习内容总结

第十二章优先队列与堆

一、堆：具有两个附加属性的一颗二叉树

它是一颗完全树
对每一结点，它小于或等于其左右孩子（或大于等于其左右孩子）
最小堆：对每一结点，它小于或等于其左右孩子
最大堆：对每一结点，它大于或等于其左右孩子
最小堆将其最小元素存储在二叉树的根处，且其根的两个孩子同样也是最小堆
最大堆将其最大元素存储在二叉树的根处，且其根的两个孩子同样也是最大堆

堆是二叉树的扩展，继承了二叉树的所有操作

addElement操作

addElcment方法将给定的元素添加到堆中的恰当位置处，且维持该堆的完全性属性和有序属性
如果给定元素不是 Comparable的，则该方法将抛出一个 ClasscastException异常。
完全属性是指：如果一棵二又树是平衡的，即所有叶子都位于h或h-1层，其中h为log2 n，且n是树中的元素数目，以及所有h层中的叶子都位于该树的左边，那么该树就被认为是完全的
增加元素的两种可能性（如图）：
因为一个堆就是一棵完全树，所以对于插入的新结点而言只存在一个正确的位置：
要么是h层左边的下一个空位置（即最后一层未满，将插入到最左边的位置）
要么是h+1层左边的第1个位置(如果h层已满)

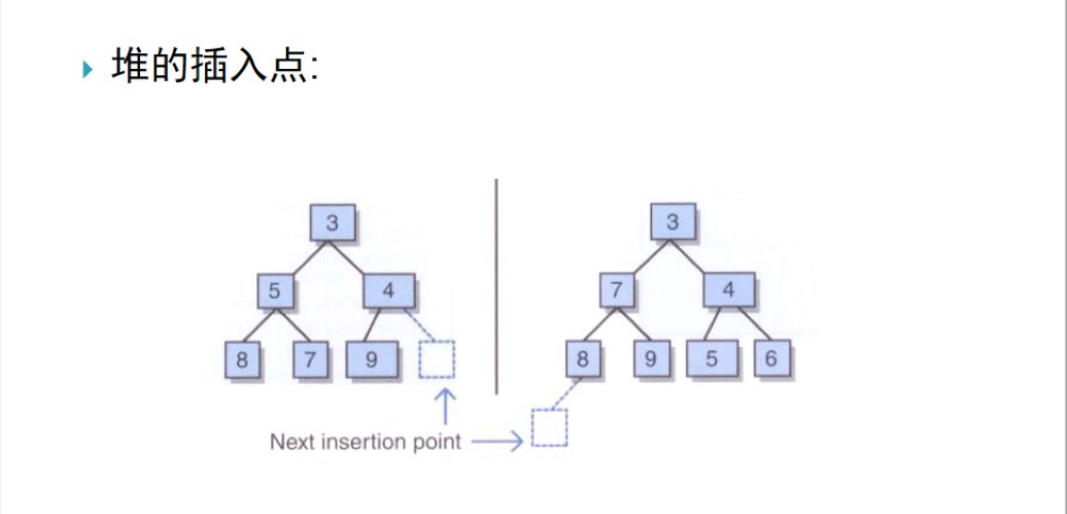
当新结点插入到正确位置之后，就要考虑到排序属性（即将堆调整为大顶堆或小顶堆）
当调整的类型是小顶堆时，做法如下（下图为调整过程）：
只需将该新值和其双亲值进行比较，如果该新结点小于其双亲则将它们互换，我们沿着树向上继续这一过程，直至该新值要么是大于其双亲要么是位于该堆的根处

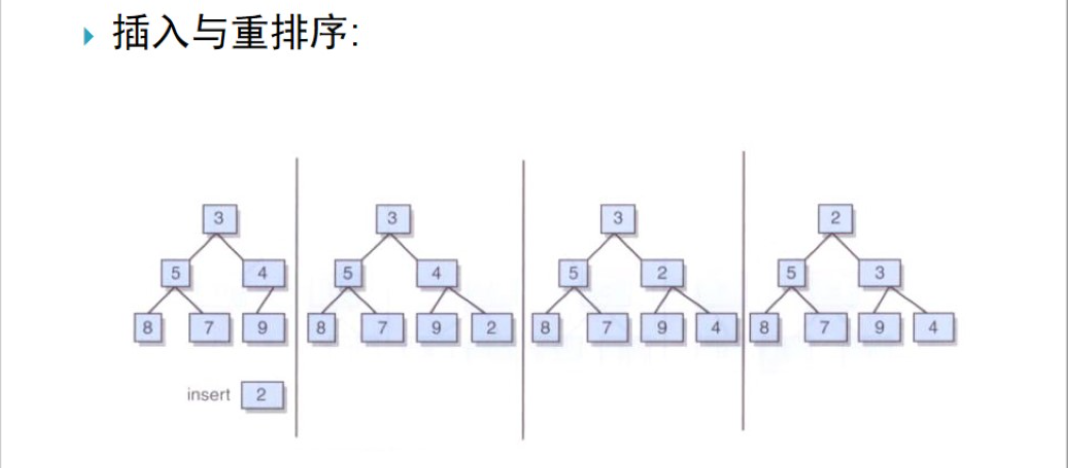
通常，在堆实现中，会对树中的最末一片叶子进行跟踪记录

removeMin操作

removeMin方法将删除最小堆中的最小元素并返回它
最小元素是存储在最小堆的根处的，所以我们需要返回存储在根处的元素并用堆中的另一元素替换它
与addElement操作一样，是要维持该树的完全性，那么只有一个能替换根的合法元素，且它是存储在树中最末一片叶子上的元素
该最末一片叶子将是树中h层上最右边的叶子
替换之后，还要对堆进行调整操作，即变成最小堆（维持有序属性）

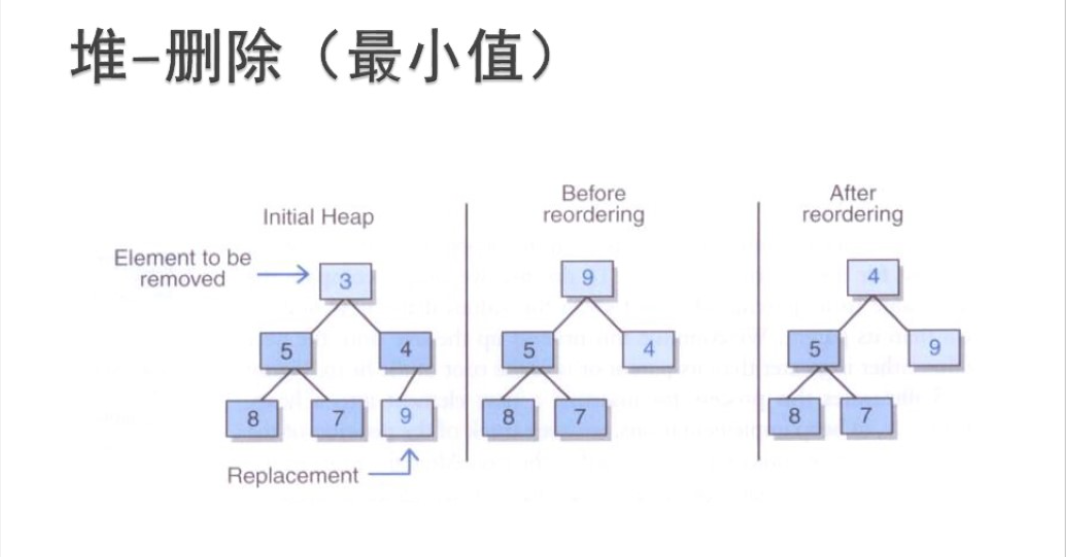
findMin操作：返回一个指向该最小堆中最小元素的引用（该元素总是被存储在树根处，所以直接返回存储在根处的元素即可）

二、使用堆：优先级队列

优先级队列就是遵循两个排序规则的集合：
第一，具有更高优先级的项目在先
第二，具有相同优先级的项目使用先进先出方法来确定其排序
优先级队列具有多种应用(比如,操作系统中的任务调度,网络中的通信调度,甚至是汽车维修处的作业调度)
可以使用某一队列列表(其中每一队列都表示了给定优先级的项目)来实现一个优先级队列
（这一问题的另一解决方案是使用一个最小堆）
按照优先级对堆排序完成了第一次排序(高优先级的项目在先)。但是，我们必须对具有相同优先级项目的先进先出排序进行操纵：
解决方案是创建一个 PriorityQueueNode对象，它存储的是将被放置在队列中的元素，该元素的优先级，以及元素放进队列的顺序
然后,我们只需为 PriorityNode类定义个 compareTo方法，以便先对优先级进行比较，然后在优先级一样的时候再对阶进行比较

三、用链表实现堆

堆的链表实现要求在插入元素后能够向上遍历该树，所以堆中的结点必须存储指向其双亲的指针
BinaryTreeNode类没有双亲指针，所以创建一个HeapNode类链表实现（对BinaryTreeNode进行扩展并添加一个双亲指针）

addElement操作
addElement必须完成三个任务：

* 在恰当位置处添加一个新元素
* 对堆进行重排序以维持其排序属性
* 将lastNode指针重新设定为指向新的最末结点

removeMin操作
removeMin方法必须完成三个任务：

* 用存储在最末结点处的元素替换存储在根处的元素
* 对堆进行重排序（如有必要）
* 返回初始的根元素

链表实现的removeMin方法必须删除根元素，并用来自最末结点的元素替换它

findMin操作
findMin方法仅仅返回一个指向存储在堆根处元素的引用（因此复杂度O(1) ）

四、用数组实现堆

优点：
堆的数组实现提供了一种比链表实现更为简洁的选择。
在链表实现中,我们需要上下将历树以确定树的最末一片叶子或下一个插入结点的双亲（链表实现中的许多复杂问题都与此有关）
这些困难在数组实现中就不存在了，因为通过查看存储在数组中的最末一个元素，我们就能够确定出该树中的最末结点
与链表实现堆的不同之处：
树的根位于位置0，对于每一结点n，n的左孩子将位于数组的2n+1位置处，n的右孩子将位于数组的2(n+1)位置处（反过来同样也是对的）
对于任何除了根之外的结点n，n的双亲位于(n-1)/2位置处，因为我们能够计算双亲和孩子的位置，所以与链表实现不同的是，数组实现不需要创建一个 Heap Node类
addElement操作
数组实现的addElement方法必须完成3项任务：

在恰当位置处添加新结点
对堆进行重排序以维持其排序属性
将count递增1

跟数组实现一样，该方法必须首先检查空间的可用，需要时要进行扩容

数组实现的addElement操作与链表的相同（都为O(logn)），但数组实现的效率更高

removeMin操作
removeMin方法必须完成三项任务：

用存储在最末元素处的元素替换存储在根处的元素
必要时对堆进行重排序
返回初始的根元素

链表实现和数组实现的removeMin操作的复杂度都为O(logn)

findMin操作
与链表实现的一样，findMin方法仅仅是返回一个引用，该引用指向存储在堆的根处或数组的0位置处的元素，其复杂度为O(1)

五、使用堆：堆排序

使用堆来对某个数字列表进行排序：
将列表的每一元素添加到堆中，然后次一个地将它们从根中删除，
在最小堆的情形下，排序结果将是该列表以升序排列；
在最大堆的情形下，排序结果将是该列表以降序排列
堆排序的复杂度分析：
由于添加和删除操作的复杂度都为O(log n)，因此可以得出堆排序的复杂度也是O(log n)，但是，这些操作的复杂度为O(log n)指的是在含有n个元素的列表中添加和删除一个元素。
对任一给定的结点，插入到堆的复杂度都是O(log n)，因此n个结点的复杂度将是 O(n log n)，
删除一个结点的复杂度为O(log n），因此对n个结点的复杂度为 O(n log n)
对于堆的排序算法,我们需要执行addElement和 removeElement两个操作n次，即列表中每个元素一次。因此,最终的复杂度为2 x n x logn,即 O(n log n)

教材学习中的问题和解决过程

问题1：数组实现的addElement操作与链表的相同（都为O(logn)），但数组实现的效率更高

问题1解析：

首先，先从数组和链表本身来看：
一个常见的编程问题：遍历同样大小的数组和链表，哪个比较快？
如果按照教科书上的算法分析方法，你会得出结论，这2者一样快，因为时间复杂度都是 O(n)
但是在实践中，这2者却有极大的差异：
通过下面的分析你会发现，其实数组比链表要快很多
首先介绍一个概念：memory hierarchy （存储层次结构），电脑中存在多种不同的存储器，如下表

各级别的存储器速度差异非常大，CPU寄存器速度是内存速度的100倍！这就是为什么CPU产商发明了CPU缓存。而这个CPU缓存，就是数组和链表的区别的关键所在。

CPU缓存会把一片连续的内存空间读入，因为数组结构是连续的内存地址，所以数组全部或者部分元素被连续存在CPU缓存里面，平均读取每个元素的时间只要3个CPU时钟周期。
而链表的节点是分散在堆空间里面的，这时候CPU缓存帮不上忙，只能是去读取内存，平均读取时间需要100个CPU时钟周期。
这样算下来，数组访问的速度比链表快33倍！这里只是介绍概念，具体的数字因CPU而异）

【参考资料】
从cpu和内存来理解为什么数组比链表查询快

问题2：用堆来实现优先级队列的代码分析，书上只简单介绍了，没有具体说说代码的实现，简单分析一下

问题2解析：

优先级队列是在队列的基础上增加限制的，所以在理解了优先级队列的代码后，PP12.1就很好做了
课本通过两个类完成了堆实现的优先级队列

第一个PrioritizedObject类：
PrioritizedObject对象表示优先队列中的一个节点，包含一个可比较的对象、到达顺序和优先级值
代码如下：

   public T getElement() 
    {
        return element;//返回节点值
    }
    
    public int getPriority() 
    {
        return priority;//返回节点优先级
    }

    public int getArrivalOrder() 
    {
        return arrivalOrder;//返回到节点的距离顺序
    }

PrioritizedObject最重要的方法是优先级的比较：
代码如下：

public int compareTo(PrioritizedObject obj) //如果此对象的优先级高于给定对象，则返回1，否则返回-1
    {
      int result;
				
      if (priority > obj.getPriority())
          result = 1;
      else if (priority < obj.getPriority())
          result = -1;
      else if (arrivalOrder > obj.getArrivalOrder())
          result = 1;
      else
          result = -1;
      
      return result;
    }

先比较元素的优先级，高的先输出；
如果优先级一样，再根据先进先出的方式把距离节点近的先输出

第二个就是PriorityQueue类：
首先是添加操作：

public void addElement(T object, int priority)
    {
        PrioritizedObject<T> obj = new PrioritizedObject<T>(object, priority);
	    super.addElement(obj);
    }

声明PrioritizedObject变量之后，即确定了添加元素及其优先级
这里就直接调用了堆的addElement方法，完成添加功能

然后是删除操作：直接调用堆的删除最小值的方法，因为最小的元素是在堆顶处的，即队列的头部

public T removeNext() //从优先级队列中删除下一个最高优先级元素并返回对它的引用
    {
        PrioritizedObject<T> obj = (PrioritizedObject<T>)super.removeMin();
        return obj.getElement();
    }

代码运行中的问题及解决过程

问题1：课后编程PP12.1，用堆来实现队列，刚看完课本，都是用链表啊，数组啊来实现堆的，这题要用堆来实现队列，是要用链表或数组实现的堆来实现队列？能用队列来实现堆吗？课本上也有堆的一个应用：实现优先级队列，额，优先级队列和队列有什么不一样吗？

问题1解决过程：

首先解决一下最后一个问题：优先级队列和队列
课本的定义：优先级队列遵循两个排序规则的集合：具有更高优先级的项目在先，具有相同优先级的项目使用先进先出方法来确定其排序
百度的资料：
普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除
在优先队列中，元素被赋予优先级：当访问元素时，具有最高优先级的元素最先删除，优先队列具有最高级先出

感觉很奇怪，但是仔细想了一下：
队列只要满足队尾加元素，队头删除元素就行了，对队列中的元素顺序没有要求，只要在下次删除元素前，按照优先级把元素排好就行了把
（就像医院排队挂号一样：要考虑到军人这一优先级的存在，要先于其他人输出）

这一题就不用考虑到优先这一条件了

然后第二个问题，能用队列来实现堆吗？
这个问题。。。先留在这里。。。哈哈哈哈哈。。。我再想想
现在用堆来实现队列
正如上面教材问题里总结的：
在明白了优先级队列的实现思路后，只要把其类里的形参Priority删掉即可，即去掉优先级比较的这一操作
测试结果如下：

【参考资料】
百度百科
 优先级队列和队列有什么区别？

本周错题

本周无错题

代码托管

结对及互评

博客中值得学习的或问题：
- 侯泽洋同学的博客排版工整，界面很美观，并且本周还对博客排版、字体做了调整，很用心
- 问题总结做得很全面：对课本上不懂的代码会做透彻的分析，即便可以直接拿过来用而不用管他的含义
- 对教材中的细小问题都能够关注，并且主动去百度学习
- 代码中值得学习的或问题：
- 对于编程的编写总能找到角度去解决
本周结对学习情况
- 20172302
- 结对学习内容
  - 第十二章内容：优先队列与堆

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	4/4
第二周	560/560	1/2	6/10
第三周	415/975	1/3	6/16
第四周	1055/2030	1/4	14/30
第五周	1051/3083	1/5	8/38
第六周	785/3868	1/6	16/54
第七周	733/4601	1/7	20/74
第八周	2108/6709	1/8	20/74

posted @ 2018-11-10 18:07 20172308周亚杰阅读(260) 评论(2) 编辑收藏举报

刷新页面返回顶部

20172308周亚杰