20172308 《程序设计与数据结构》第七周学习总结
教材学习内容总结
第 十一 章 二叉查找树
一、概述
二叉查找树是一种含有附加属性的二叉树,即其左孩子小于父结点,父结点小于或等于右孩子
(二叉查找树的定义是二叉树定义的扩展)
二、 用链表实现二叉查找树
-
addElement操作:
addElement方法根据给定元素的值,在树中的恰当位置添加该元素,如果这个元素不是 comparable,则addElement方法会抛出NoComparableElemementException;
如果树为空,则这个新元素就将成为根结点;
如果树非空,这个新元素会与树根元素进行比较:
如果它小于根结点中存储的那个元素且根的左孩子为null,则这个新元素就将成为根的左孩子。
如果这个新元素小于根结点中存储的那个元素且根的左孩子不是null,则会遍历根的左孩子,并再次进行比较操作;
如果这个新元素大于或等于树根存储的那个元素且根的右孩子为null,则这个新元素会成为根的右孩子,
如果这个新元素大于或等于树根处存储的那个元素且根的右孩子不是null,则会遍历根的右孩子,并再次进行比较操作
如图:
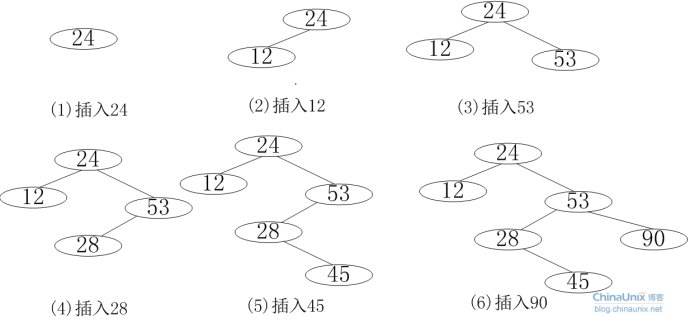
-
removeElemen操作
removeElement方法负责从二叉查找树中删除给定的 Comparable元素;或者,当在树中找不到给定目标元素时,则抛出 Element Not FoundException异常;
与前面的线性结构研究不同,这里不能简单地通过删除指定结点的相关引用指针而删除该结点;
相反,这里必须推选出另一个结点来代替要被删除的那个结点,受保护方法 replacement返回指向一个结点的引用,该结点将代替要删除的结点;
选择替换结点的三种情况如下:
- 如果被删除结点没有孩子,则 replacement返回null
- 如果被删除结点只有一个孩子,则 replacement返回这个孩子
- 如果被删除结点有两个孩子,则 replacement会返回中序后继者(因为相等元素会放到右边)

- replace方法
代码如下:
private BinaryTreeNode<T> replacement(BinaryTreeNode<T> node) {
BinaryTreeNode<T> result = null;
if ((node.left == null) && (node.right == null)) {
result = null;
} else if ((node.left != null) && (node.right == null)) {
result = node.left;
} else if ((node.left == null) && (node.right != null)) {
result = node.right;
} else {
BinaryTreeNode<T> current = node.right;// 初始化右侧第一个结点
BinaryTreeNode<T> parent = node;
// 获取右边子树的最左边的结点
while (current.left != null) {
parent = current;
current = current.left;
}
current.left = node.left;
// 如果当前待查询的结点
if (node.right != current) {
parent.left = current.right;// 整体的树结构移动就可以了
current.right = node.right;
}
result = current;
}
return result;
}
-
removeAllOccurrences操作
removeAllOccurrences方法负责从二叉查找树中删除指定元素的所有存在;
或者,当在树中找不到指定元素时,则抛出 ElementNotFoundException异常;
如果指定的元素不是Comparable,则removeAllOccurrences方法也会抛出 ClassCastException异常,该方法会调用一次 removeElement方法,以此确保当树中根本不存在指定元素时会抛出异常,
只要树中还含有目标元素,就会再次调用 removeElement方法,注意, removeAllOccurrences方法使用了 LinkedBinaryTree类的 contans方法,还要注意,在 LinkedBinaryTree类中的find方法已经被重载了,以便利用二又查找树的有序属性 -
removeMin操作
最小元素在二又查找树中的位置有3种可能情形:
- 如果树根没有左孩子,则树根就是最小元素,而树根的右孩子会变成新的根结点
- 如果树的最左侧结点是一片叶子,则这片叶子就是最小元素,这时只需设置其父结点的左孩子引用为mul即可
- 如果树的最左侧结点是一个内部结点,则需要设置其父结点的左孩子引用指向这个将删除结点的右孩子
三、用有序列表实现二叉查找树
- 树的主要使用之一就是为其他集合提供高效的实现
- 我们假定 BinarySearchTreeList实现中用到的 LinkedBinarySearchTree实现是一种带有附加属性的平衡二叉查找树,这种附加属性是:任何结点的最大深度为log2 n其中n为树中存储的元素数目。
在我们的平衡二又查找树假设之下,add操作和remove操作都要求重新平衡化树,这一点根据所使用的算法会对分析有所影响。
另外还要注意一点:虽然树实现中的有些操作更为有效,比如 removelast,last和contains,但在利用树实现时,也有一些操作会变得低效,比如 removeFirst和first
四、平衡二叉查找树
-
如果二叉查找树不平衡,其效率可能比线性结构的还要低
-
蜕化树:看起来更像一个链表,但实际上它的效率比链表的还低,因为每个结点还附带额外的开销
如图(b)所示:
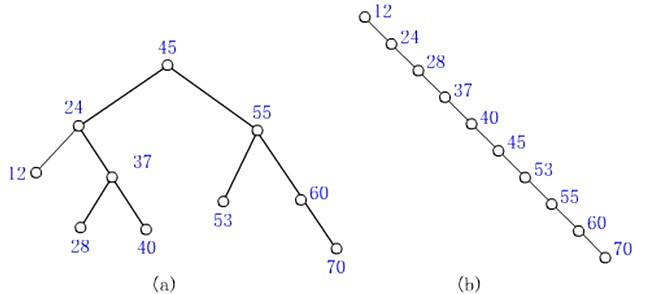
-
平衡化技术
-
右旋
要平衡化该树,我们需要:
使树根的左孩子元素成为新的根元素
使原根元素成为这个新树根的右孩子元素。
使树根的左孩子的右孩子,成为原树根的新的左孩子

-
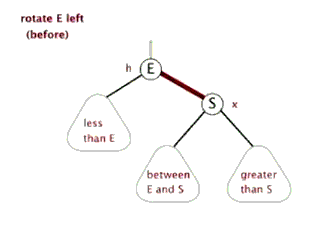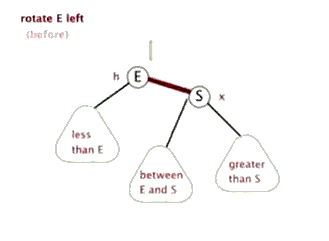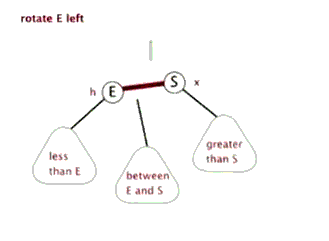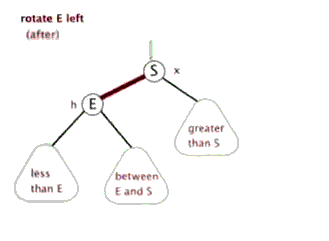
左旋
要平衡化该树,我们需要:
使树根的右孩子元素成为新的根元素
使原根元素成为这个新树根的左孩子元素。
使原树根右孩子结点的左孩子,成为原树根的新的右孩子。
-
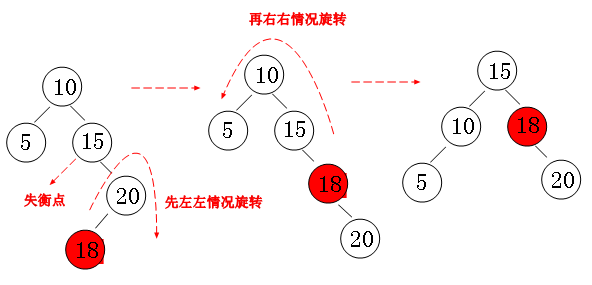
右左旋
并非所有的不平衡问题都可以只进行某一种旋转就能解决
对于由树根右孩子的左子树中较长路径而导致的不平衡,
我们必须先让树根右孩子的左孩子,绕着树根的右孩子进行一次右旋,然后再让所得的树根右孩子绕着树根进行一次左旋
-
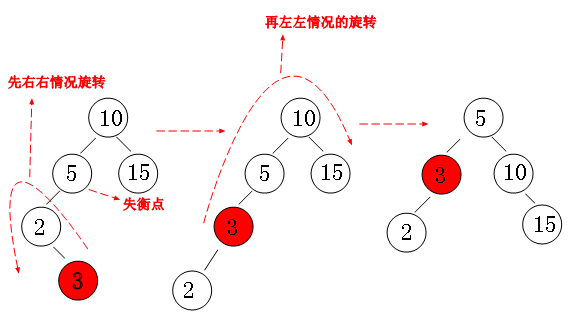
左右旋
对于由树根左孩子的右子树中较长路径而导致的不平衡,
我们必须先让树根左孩子的右孩子绕着树根的左孩子进行一次左旋,然后再让所得的树根左孩子绕着树根进行一次右旋
五、实现二叉查找树:AVL树
- 对于树中的任何结点,如果其平衡因子(其左右子树的高度差大于1或小于-1),则以该结点为树根的子树需要重新平衡
- 树只有两种途径变得不平衡:插入或删除结点,因此每次进行这两种操作后都必须更新平衡因子,然后从操作的结点处检查树的平衡性,一直检查上溯至根结点
因此:AVL树通常实现为每个结点都包含一个指向其父结点的引用
六、实现二叉查找树:红黑树
(1). 红黑树:一种平衡二叉查找树,其中的每个结点存储一种颜色(红或黑,用布尔值实现,false等价于红色)
控制结点颜色的规则:
- 根结点为黑色
- 红色结点的所有孩子都为黑色
- 从树根到树叶的每条路径都包含同样数目的黑色结点

(2). 在某种程度上,红黑树的平衡限制没有AVL树那么严格,但是,他们的序仍然是logn
(3). 红黑树中的元素插入
红黑树的插入操作类似于前面的addElement方法,但是这里总是把插入的新元素颜色设置为红色,
插入新元素之后,必要时将重新平衡化该树,根据需要改变元素的颜色以便维持红黑树的属性
- 红黑树插入元素之后的重新平衡化是一个迭代过程,该迭代过程的终止条件有两种形式:
形式1:current == root (current是当前正在处理的结点)
我们总是设置根结点颜色为黑色,而所有路径都包括树根,因此不能违背各条路径都拥有同样数目黑色元素这一规则
形式2:current.parent.color == black(即当前结点的父结点颜色为黑色)
current所指向的结点总是一个红色结点,这意味着,如果当前结点的父结点是黑色,则可满足所有规则,因为红色结点并不影响路径中的黑色结点数目;
另外由于是从插入点处上溯处理,因此早已平衡了当前结点下面的子树
- 重新平衡化的每次迭代,我们都关注于如何着色当前结点的兄弟结点:
当前结点的父结点只有两种可能:左孩子或右孩子
可能一:
如果是左孩子,利用 current.parent.parent.left.color 得到颜色信息(null元素的颜色为黑色),且存在两种情况:
父结点的兄弟为红色或黑色:这两种情况下,我们阐述的处理步骤都将发生在一个循环内部(该循环的终止条件如前所述)
如果父结点的兄弟为红色,这时的处理步骤如下:
设置current的父亲的颜色为 black
设置父结点的兄弟的颜色为black
设置 current的祖父的颜色为red
设置 current指向current的祖父
如果父结点的兄弟为黑色,首先要查看current是左孩子还是右孩子:
如果current是右孩子,则必须设置current等于其父亲,在继续之前还要再向左旋转current.right;
后面的步骤,与开始时current为左孩子一样
如果current是左孩子:
设置current的父亲的颜色为black
设置current的祖父的颜色为red
如果current的祖父不等于null,则让current的父亲绕着current的祖父向右旋转
可能二:
如果是右孩子,存在两种情况:
父结点的兄弟为红色或黑色:这两种情况下,我们阐述的处理步骤都将发生在一个循环内部(该循环的终止条件如前所述)
如果父结点的兄弟为红色,这时的处理步骤如下(同当前结点的父结点的兄弟颜色为红时):
设置current的父亲的颜色为 black
设置父结点的兄弟的颜色为black
设置 current的祖父的颜色为red
设置 current指向current的祖父
如果父结点的兄弟为黑色,首先要查看current是左孩子还是右孩子(与当前结点的父结点的兄弟颜色为黑时,操作对称):
如果current是左孩子,则必须设置current等于其父亲,在继续之前还要再向右旋转current.left;
后面的步骤,与开始时current为右孩子一样
如果current是右孩子:
设置current的父亲的颜色为black
设置current的祖父的颜色为red
如果current的祖父不等于null,则让current的父亲绕着current的祖父向左旋转
(4). 红黑树中的元素删除
与元素插入的那些情况一样,删除的两种情况也是对称的——取决于 current是左孩子还是右孩子。
当 current为右孩子时:
(在插入时,我们最关注的是当前结点的父亲的兄弟的颜色)
而对删除而言,焦点要放在当前结点的兄弟的颜色上(用 current.parent. left.color来指代这种颜色):
还要观察该兄弟的孩子的颜色,要注意的重要一点是:颜色的默认值是black;
这样,任何时刻如果试图取得mull对象的颜色,结果都将是black
其他的情况很容易推导出来,只要把上述情况中的“左”换成“右”、“右”换成“左”即可
如果兄弟的颜色是red,则在做其他事之前必须完成如下处理步骤:
* 设置兄弟的颜色为black
* 设置current的父亲的颜色为red
* 让兄弟绕着 current的父亲向右旋转
* 设置兄弟等于 current的父亲的左孩子
下面再继续处理过程:不管这个初始兄弟是red还是 black,这里的处理会根据兄弟的孩子的颜色分成两种情况:
如果兄弟的两个孩子都是black(或null),则需要
* 设置兄弟的颜色为red
* 设置 current等于 current的父亲
如果兄弟的两个孩子不全为black,则将查看兄弟的左孩子是否是black,如果是,则在继续之前必须完成如下步骤:
* 设置兄弟的右孩子的颜色为 black
* 设置兄弟的颜色为red
* 让兄弟的右孩子绕着兄弟本身向右旋转
* 设置兄弟等于cumt的父亲的左孩子
最后是兄弟的两个孩子都不为 black这一情况,这时必须:
* 设置兄弟的颜色为 current的父亲的颜色。
* 设置 current的父亲的颜色为black
* 设置兄弟的左孩子的颜色为black
* 让兄弟绕着 current的父亲向右旋转
* 设置 current等于树根
该循环终止之后,我们要酬除该结点,并设置其父亲的孩子引用为mull
教材学习中的问题和解决过程
问题1:红黑树这样设计的意义在哪里呢?
问题1解析:
现在所明白的是红黑树是为了让二叉树路径不会过长而导致查找等操作的效率过低,通过红黑结点的限制,使得红黑树的最大长度约为2logn
但是对于红黑树的设计思想来源不是很明白,为什么要这样设计,以及这样设计真的能达到效果,真的是对的嘛?
像AVL树那样,每次插入删除都要进行旋转使得树平衡,这不就够了吗?为什么还要再弄一个红黑树?
百度了相关的资料,然后总结汇总在这里:
- 首先要知道红黑树的起源(即设计来源):
红黑树的起源,自然是二叉查找树了,这种树结构从根节点开始,左子节点小于它,右子节点大于它
每个节点都符合这个特性,所以易于查找,是一种很好的数据结构
但是它有一个问题,就是容易偏向某一侧,这样就像一个链表结构了(如图),失去了树结构的优点,查找时间会变坏
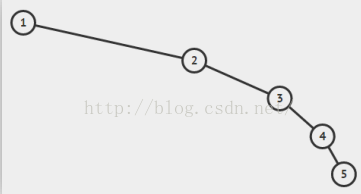
在这种需求下,平衡树的概念就应运而生了
红黑树就是一种平衡树,它可以保证二叉树基本符合矮矮胖胖的结构,
但是理解红黑树之前,必须先了解另一种树,叫2-3树,即红黑树背后的逻辑(以下2-3树的介绍来自CSDN博客清晰理解红黑树的演变---红黑的含义)
2-3树是二叉查找树的变种,树中的2和3代表两种节点,以下表示为2-节点和3-节点。
2-节点即普通节点:包含一个元素,两条子链接
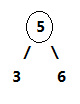
3-节点则是扩充版,包含2个元素和三条链接:两个元素A、B,左边的链接指向小于A的节点,中间的链接指向介于A、B值之间的节点,右边的链接指向大于B的节点。
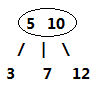
在这两种节点的配合下,2-3树可以保证在插入值过程中,任意叶子节点到根节点的距离都是相同的。完全实现了矮胖矮胖的目标。怎么配合的呢,下面来看2-3树的构造过程。
所谓构造,就是从零开始一个节点一个节点的插入。
在二叉查找树中,插入过程从根节点开始比较,小于节点值往右继续与左子节点比,大于则继续与右子节点比,直到某节点左或右子节点为空,把值插入进去。这样无法避免偏向问题。在2-3树中,插入的过程是这样的。
如果将值插入一个2-节点,则将2-节点扩充为一个3-节点。
如果将值插入一个3-节点,分为以下几种情况。
(1).3-节点没有父节点,即整棵树就只有它一个三节点。此时,将3-节点扩充为一个4-节点,即包含三个元素的节点,然后将其分解,变成一棵二叉树。

此时二叉树依然保持平衡。
(2).3-节点有一个2-节点的父节点,此时的操作是,3-节点扩充为4-节点,然后分解4-节点,然后将分解后的新树的父节点融入到2-节点的父节点中去。

(3).3-节点有一个3-节点的父节点,此时操作是:3-节点扩充为4-节点,然后分解4-节点,新树父节点向上融合,上面的3-节点继续扩充,融合,分解,新树继续向上融合,直到父节点为2-节点为止,如果向上到根节点都是3-节点,将根节点扩充为4-节点,然后分解为新树,至此,整个树增加一层,仍然保持平衡。
第三种情况稍微复杂点,为了便于直观理解,现在我们从零开始构建2-3树,囊括上面所有的情况,看完所以步骤后,你也可以自己画一画。
我们将{7,8,9,10,11,12}中的数值依次插入2-3树,画出它的过程:
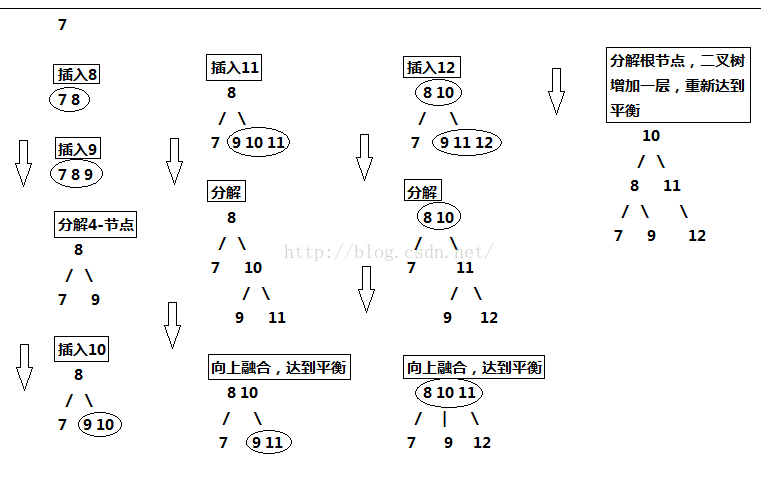
所以,2-3树的设计完全可以保证二叉树保持矮矮胖胖的状态,保持其性能良好。但是,将这种直白的表述写成代码实现起来并不方便,因为要处理的情况太多。这样需要维护两种不同类型的节点,将链接和其他信息从一个节点复制到另一个节点,将节点从一种类型转换为另一种类型等等。
因此,红黑树出现了,红黑树的背后逻辑就是2-3树的逻辑,但是由于用红黑作为标记这个小技巧,最后实现的代码量并不大。(但是,要直接理解这些代码是如何工作的以及背后的道理,就比较困难了。所以你一定要理解它的演化过程,才能真正的理解红黑树)
看看红黑树和2-3树的关联,首先,红和黑的含义:红黑树中,所有的节点都是标准的2-节点,为了体现出3-节点,这里将3-节点的两个元素用左斜红色的链接连接起来,即连接了两个2-节点来表示一个3-节点。这里红色节点标记就代表指向其的链接是红链接,黑色标记的节点就是普通的节点。所以才会有那样一条定义,叫“从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点”,因为红色节点是可以与其父节点合并为一个3-节点的,红黑树实现的其实是一个完美的黑色平衡,如果你将红黑树中所有的红色链接放平,那么它所有的叶子节点到根节点的距离都是相同的。所以它并不是一个严格的平衡二叉树,但是它的综合性能已经很优秀了。
【参考资料】
清晰理解红黑树的演变---红黑的含义
代码运行中的问题及解决过程
问题1:在编写课后项目PP11.3时,关于removeMax的操作有点理解不到位,现在详细分析一下代码,理清思路
问题1解决过程:
二叉查找树是有特定属性的,即一个结点的左孩子小于当前结点,当前结点又小于等于其右孩子的
所以一棵树,最大值一定在树的最右边,最小值在树的最左边,在此基础上可以分析代码:
- 首先:判断是否为空,空则抛出异常
- 然后:
树不空,判断树根的右孩子是否为空,空则当前根元素即为最大值;
树根的右孩子如果不空的话,就要利用递归,一直找到树最右边的孩子,返回这个元素,并删除它 - 代码如下:
public T removeMax() {
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");//判断树是否为空,空则抛出异常
else {//不空的话,则判断树根的右孩子是否为空
if (root.right == null) {//根的右孩子为空,则最大值即为根元素,然后执行删除根元素操作
result = root.element;
root = root.left;//让根的左孩子等于根,即完成删除操作
} else {//根的右孩子不为空,则执行递归操作,一直找到整棵树最右边的元素(即最大元素)
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null) {
parent = current;
current = current.right;
}
result = current.element;//找到最大元素current,赋给result
parent.right = current.left;//把要删除的元素的左孩子赋给要删除元素的双亲的右孩子,即完成删除当前元素的操作
}
modCount--;
}
return result;
}
这个删除最大值的代码与找最大值最小值的操作findMin,findMax差不多,都是一样的思路,只是找到之后,不会进行删除操作而已
如下是找最大值的代码实现,最小值的实现与之对称:
public T findMax() {
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else {
if (root.right == null) {
result = root.element;
} else {
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null) {
parent = current;
current = current.right;
}
result = current.element;
}
}
return result;
}
最后的结果运行如图:
问题2:课后项目PP11.8,将一颗二叉树变成一颗AVL树:如何将一颗二叉树变成一颗AVL树?
问题2解决过程:
首先要理解什么是AVL树,什么样的树算AVL树
树都是用来存储数据的,普通的二叉树可以按照要求在任一可以放置孩子的结点处放置结点
而AVL树对放置结点的位置有要求,即放置完后会对结点进行调整,左旋、右旋,使树达到平衡
并且导致二叉树失衡的可能只有两种操作:插入、删除
所以设计的关键在于:如何通过旋转,使得失衡点处重新平衡
根据书上的介绍,旋转一共有四种情况:左旋,右旋,左右旋,右左旋,以满足对失衡点处的失衡情况的可能性分析
即四种旋转情况对应四种可能的失衡情况:
假设结点X为失衡点:(原先的二叉树代码中没有删除操作,这里也只讨论插入带来的失衡问题)
① 在结点X的左孩子结点的左子树中插入元素
② 在结点X的左孩子结点的右子树中插入元素
③ 在结点X的右孩子结点的左子树中插入元素
④ 在结点X的右孩子结点的右子树中插入元素
参照上面课本知识梳理中四种旋转的平衡化技术,对应这四种情况:第①情况和第④情况是对称的,可以通过单旋转来解决,而第②种情况和第③情况是对称的,需要双旋转来解决
左单旋代码实现:
private AVLNode<T> singleRotateLeft(AVLNode<T> x){
//把w结点旋转为根结点
AVLNode<T> w= x.left;
//同时w的右子树变为x的左子树
x.left=w.right;
//x变为w的右子树
w.right=x;
//重新计算x/w的高度
x.height=Math.max(height(x.left),height(x.right))+1;
w.height=Math.max(height(w.left),x.height)+1;
return w;//返回新的根结点
}
右单旋代码实现:
private AVLNode<T> singleRotateRight(AVLNode<T> w){
AVLNode<T> x=w.right;
w.right=x.left;
x.left=w;
//重新计算x/w的高度
w.height=Math.max(height(w.left),height(w.right))+1;
x.height=Math.max(height(x.left),w.height)+1;
//返回新的根结点
return x;
}
利用上面写好的代码可以直接用于双旋的情况:
左右旋代码实现:
private AVLNode<T> doubleRotateWithLeft(AVLNode<T> x){
//w先进行RR旋转
x.left=singleRotateRight(x.left);
//再进行x的LL旋转
return singleRotateLeft(x);
}
右左旋代码实现:
private AVLNode<T> doubleRotateWithRight(AVLNode<T> x){
//先进行LL旋转
x.right=singleRotateLeft(x.right);
//再进行RR旋转
return singleRotateRight(x);
}
平衡化技术的代码实现之后,再实现插入操作即可,但是要分两步(因为是AVL树嘛):
首先因为是二叉查找树嘛,肯定要对要插入的元素找到合适的位置嘛。。。(这里跟二叉树一样可以用递归算法来找)
然后呢就是平衡判断,判断插入元素之后,树是否平衡(只要评估子树即可),不平衡则通过上述的四种旋转来使树重新平衡
插入操作的代码如下:
public void insert(T data) {
if (data==null){
throw new RuntimeException("data can\'t not be null ");
}
this.root=insert(data,root);
}
private AVLNode<T> insert(T data , AVLNode<T> p){
//说明已没有孩子结点,可以创建新结点插入了.
if(p==null){
p=new AVLNode<T>(data);
}else if(data.compareTo(p.data)<0){//向左子树寻找插入位置
p.left=insert(data,p.left);
//插入后计算子树的高度,等于2则需要重新恢复平衡,由于是左边插入,左子树的高度肯定大于等于右子树的高度
if(height(p.left)-height(p.right)==2){
//判断data是插入点的左孩子还是右孩子
if(data.compareTo(p.left.data)<0){
//进行LL旋转
p=singleRotateLeft(p);
}else {
//进行左右旋转
p=doubleRotateWithLeft(p);
}
}
}else if (data.compareTo(p.data)>0){//向右子树寻找插入位置
p.right=insert(data,p.right);
if(height(p.right)-height(p.left)==2){
if (data.compareTo(p.right.data)<0){
//进行右左旋转
p=doubleRotateWithRight(p);
}else {
p=singleRotateRight(p);
}
}
}
else
;//if exist do nothing
//重新计算各个结点的高度
p.height = Math.max( height( p.left ), height( p.right ) ) + 1;
return p;//返回根结点
}
【参考资料】
二叉树与AVL树
java数据结构与算法之平衡二叉树(AVL树)的设计与实现
本周错题
错题1:
错题1解析:选择排序通过重复地将下一个最小的元素放到最后排序的位置来对列表进行排序
错题2:
错题2解析:与错题1重复
错题3:
错题3解析:在从二叉搜索树中删除元素时,必须提升另一个节点来替换要删除的节点。
错题4:

错题4解析:与错题3重复
代码托管
结对及互评
-
博客中值得学习的或问题:
- 侯泽洋同学的博客排版工整,界面很美观,并且本周还对博客排版、字体做了调整,很用心
- 问题总结做得很全面:对课本上不懂的代码会做透彻的分析,即便可以直接拿过来用而不用管他的含义
- 对教材中的细小问题都能够关注,并且主动去百度学习
- 代码中值得学习的或问题:
- 对于编程的编写总能找到角度去解决
-
本周结对学习情况
- 20172302
- 结对学习内容
- 第十一章内容:二叉查找树
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 4/4 | |
| 第二周 | 560/560 | 1/2 | 6/10 | |
| 第三周 | 415/975 | 1/3 | 6/16 | |
| 第四周 | 1055/2030 | 1/4 | 14/30 | |
| 第五周 | 1051/3083 | 1/5 | 8/38 | |
| 第六周 | 785/3868 | 1/6 | 16/54 | |
| 第七周 | 733/4601 | 1/7 | 20/74 |


