20172308 《程序设计与数据结构》第五周学习总结

教材学习内容总结

第九章排序与查找

一、查找：在查找池中查找目标元素或确定查找池中不存在该目标元素

常见查找方式：线性查找、二分查找
高效的查找：查找过程做出的比较次数更少
线性查找（时间复杂度O（n））：不要求数组中元素有任何特定顺序；从第一个元素依次比较直至找到目标元素或到达最后一个元素得出元素不存在的结论
二分查找（时间复杂度O（log2 n））：查找元素已排序（则效率高于线性查找）
只比较目标元素与可行候选项的中间元素
然后删除一半的可行候选项（包括中间元素）
二分查找过程中可能会有偶数个待查找值，即出现两个中间值，该算法计算中间索引时会丢弃小数部分，即中间值会选择两个中间值的第一个
查找算法比较
与线性查找相比，二分查找的复杂度是对数级的，这使得它对大型查找池非常有效率
但是，线性查找一般比二分查找要简单，编程与调试更容易且无需花费额外成本排序查找列表

二、排序：基于一个标准，将一组项目按照某个顺序排列

排序算法
顺序排序：选择排序、插入排序、冒泡排序
对数排序：快速排序、归并排序
n个元素排序：顺序排序大约n^2次比较，对数排序大约nlog2 n次比较
n较小时，这两类算法几乎不存在实际差别
选择排序：

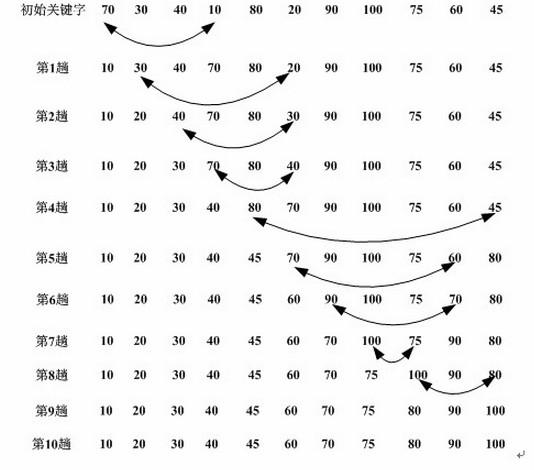
第1趟排序，在待排序数据arr[1]~arr[n]中选出最小的数据，将它与arrr[1]交换；
第2趟，在待排序数据arr[2]~arr[n]中选出最小的数据，将它与r[2]交换；
以此类推，第i趟在待排序数据arr[i]~arr[n]中选出最小的数据，将它与r[i]交换，直到全部排序完成。

插入排序：

反复地将某一特定值插入到元素列表的已排序的子集中来完成排序
需要注意的是，每次插入可能需要元素移位，并且每插入一次已排序子集都将多一个元素

冒泡排序：重复地比较相邻元素且在必要时将他们互换，从而达到排序目的

n个元素，每一轮排序都将最大值移到最终位置，需比较n-1轮；
每一轮过后，下一轮需要比较的值就会少一个
冒泡排序的算法似乎还可以设计两边一起冒。。。

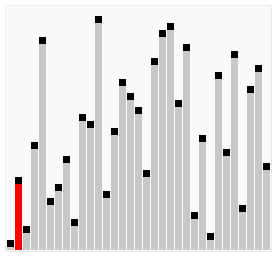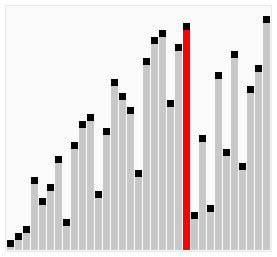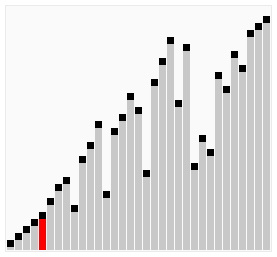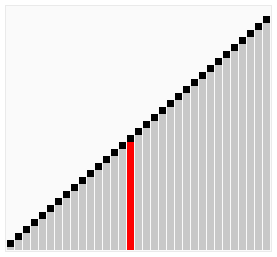
快速排序：通过使用一个任意选定的分区元素将该列表分区，然后对分区元素的任一边的子列表进行递归排序

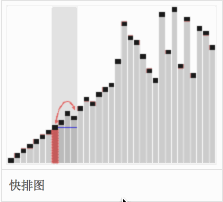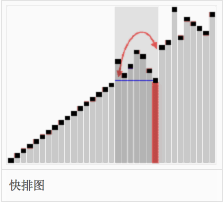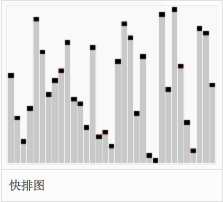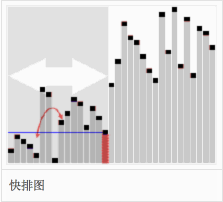
分区元素的选择是任意的，但最好选择列表的第一个元素，从而第一轮快速排序分区元素能把列表大致分为两半
持续对两个分区进快速排序，直至分区只含有一个元素，排序即完成
值得注意的是，决定放置好了初始分区元素，就不会对其进行考虑和移动了

归并排序：算法通过将列表递归分成两半直至每一子列表都含有一个元素，然后将这些子列表归并到一个排序顺序中

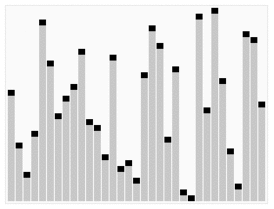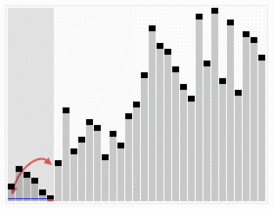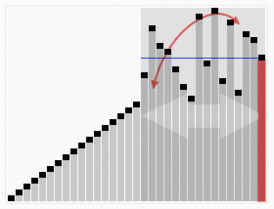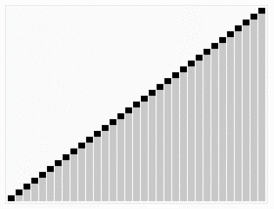
归并排序包括"从上往下"和"从下往上"2种方式
如图所示：

教材学习中的问题和解决过程

问题1：对归并排序算法的理解

问题1解析：

首先看到这个排序算法的时候，有一个疑惑：算法好像只是一半一半地将原列表元素分成只含有一个元素的子列表，然后再将只含有一个元素的子列表归并成一个新的已排好序的列表，即完成了排序。
那问题是，归并的时候是怎么把序排好的？
将两个已经有序的子序列合并成一个有序序列，比如下图中的一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，
合并为最终序列[1,2,3,4,5,6,7,8]，步骤为：

【参考资料】
图解排序算法(四)之归并排序

问题2：在总结课本知识点的时候，百度到冒泡排序还可以从两边一起冒

问题2解析：冒泡排序的改进方法（即双向冒泡）：

比较相邻两个元素的大小。如果前一个元素比后一个元素大，则两元素位置交换；
奇数趟时从左向右进行比较和交换；
偶数趟时从右向左进行比较和交换；
当从左端开始遍历的指针与从右端开始遍历的指针相遇时，排序结束；

通俗来说就是：
首先将第一个数和第二个数比较，若第二个数比第一个数小，则交换，然后比较第二第三个，并以此类推，
直到第n-1个数和第n个数比较为止，这时最大的数在第n个位置，这是第一次比较；
然后第二次比较从第n-1个数依次到第一个数，此时最小的数在第一个位置；
第三次比较则是从第二个数开始依次比较，直到第n-1个数...依次类推，直到中间两个数比较完为止

代码实现：

int arrayLength = array.length;

        int preIndex = 0;
        int backIndex = arrayLength - 1;
        while(preIndex < backIndex) {
            preSort(array, arrayLength, preIndex);
            preIndex++;

            if (preIndex >= backIndex) {
                break;
            }

            backSort(array, backIndex);
            backIndex--;
        }
    }

    // 从前向后排序
    private void preSort(int[] array, int length, int preIndex) {
        for (int i = preIndex + 1; i < length; i++) {
            if (array[preIndex] > array[i]) {
                ArrayUtils.swap(array, preIndex, i);
            }
        }
    }

    // 从后向前排序
    private void backSort(int[] array, int backIndex) {
        for (int i = backIndex - 1; i >= 0; i--) {
            if (array[i] > array[backIndex]) {
                ArrayUtils.swap(array, i, backIndex);
            }
        }

【参考资料】
排序算法系列：冒泡排序与双向冒泡排序
 排序-----冒泡排序（单向冒泡，双向冒泡，优化版本）

代码运行中的问题及解决过程

问题1：对于PP9.2的编程，一开始觉得思路不是很清晰，后来发现题目给的算法跟冒泡排序的算法好像不太一样：冒泡排序的嵌套循环，外层是控制每一轮要找到的最小元素要放置的位置，内层循环是找到每一轮最小的元素；而间隔排序的算法是内层循环都是每一轮从第一个元素开始间隔i个元素找到元素做比较，外层循环是减小i的值，然后接着内层循环

这里会出现的问题就是，间隔的元素i加上去之后可能超过数组的长度，即不存在这个元素，就会出现如图的错误：

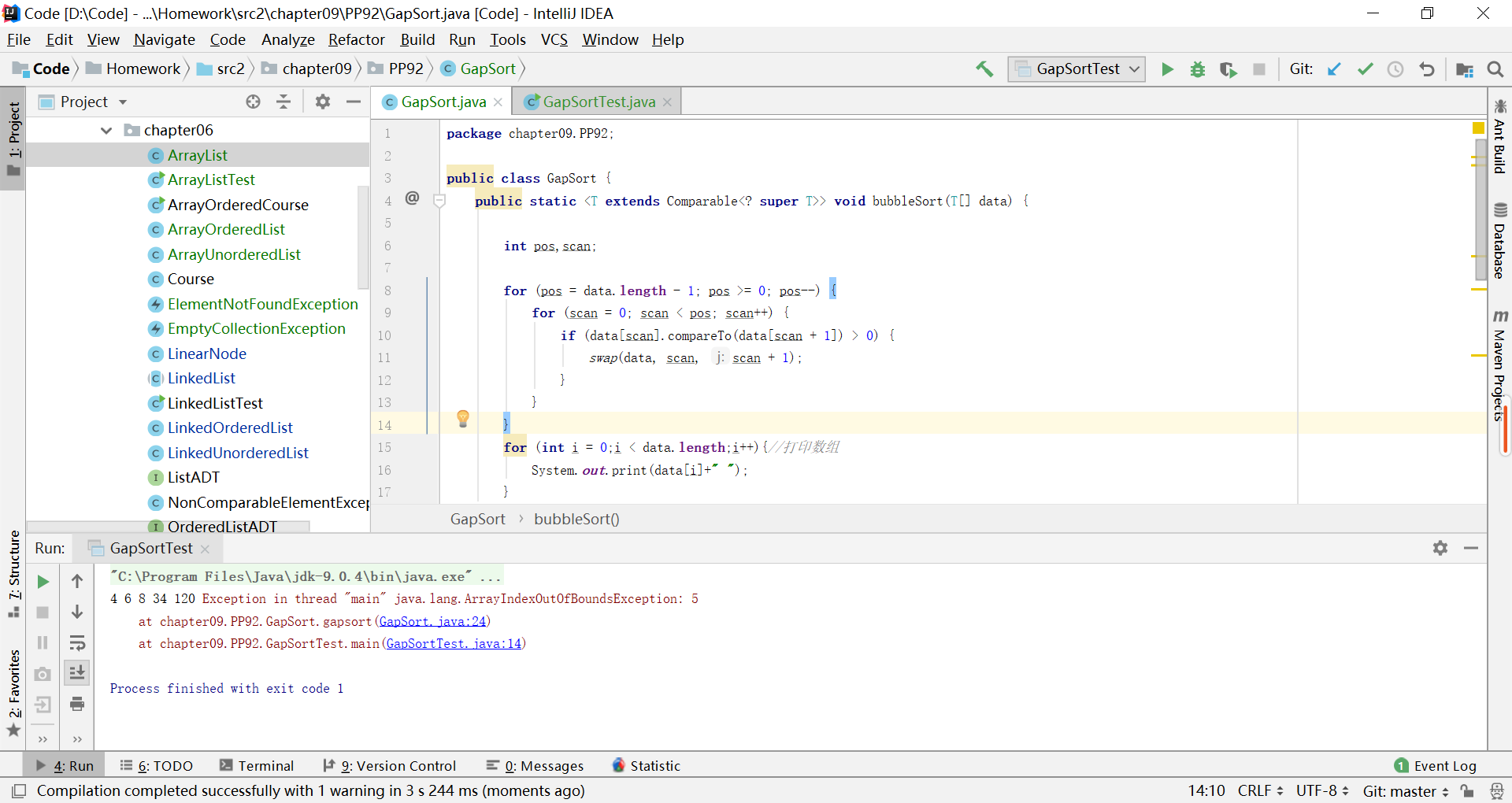
问题1解决过程：这个时候我想到的思路是：

（1）对i进行限制，先把i定义成数组的长度少一，然后在每一轮比较前先对扫描到的索引处+i是否超过数组长度，不超过则进行比较，超过则对i递减1，直到不超过数组长度
（2）也可对加i之后超过数组长度的索引处元素不予比较，紧接着比较下一索引处元素（当然这就更不可能啦。。。），也可以遇到超过数组长度的索引处元素，直接将i减1，进行下一轮循环
思路（1）代码如下：

int i,scan;
        for (i = data.length - 1;i>0;i--){
        for (scan = 0; scan < data.length - 1; scan++) {
            if (scan + i < data.length) {
                if (data[scan].compareTo(data[scan + i]) > 0)
                    swap(data, scan, scan + i);
            }

        }
        }

运行结果如图：

思路（2）的代码如下：

        int i,scan;
        for (i = data.length - 1;i>0;i--){
            for (scan = 0; scan < data.length - 1; scan++) {
                if (scan + i >= data.length)
                    continue;
                    if (data[scan].compareTo(data[scan + i]) > 0)
                        swap(data, scan, scan + i);
            }
        }

用一个if语句来判断是否间隔i个元素后过界，然后直接continue跳出循环，进行下一轮循环
运行结果跟上图一致。

【更新】
经过与侯泽洋同学的一番探讨，我发现我看题有点不仔细：
每一轮迭代中，i减少的数量是一个大于1的数
这样的话，在外层循环对i进行修改操作就没问题了；

问题2：PP9.3存在的问题是，算法的执行时间如何去记录、计算

问题2解决过程：

百度了方法之后很简单，代码如下：

long startTime=System.nanoTime();   //获取开始时间  
doSomeThing(); //测试的代码段  
long endTime=System.nanoTime(); //获取结束时间  
System.out.println("程序运行时间： "+(endTime-startTime)+"ns");

一开始用的是毫秒计算，但是结果显示都是0ms，于是换了纳秒计算；
有一个很有趣的现象，就是已经排好序的列表排序的时间甚至比没排好序的列表花费的时间还要多，如图：

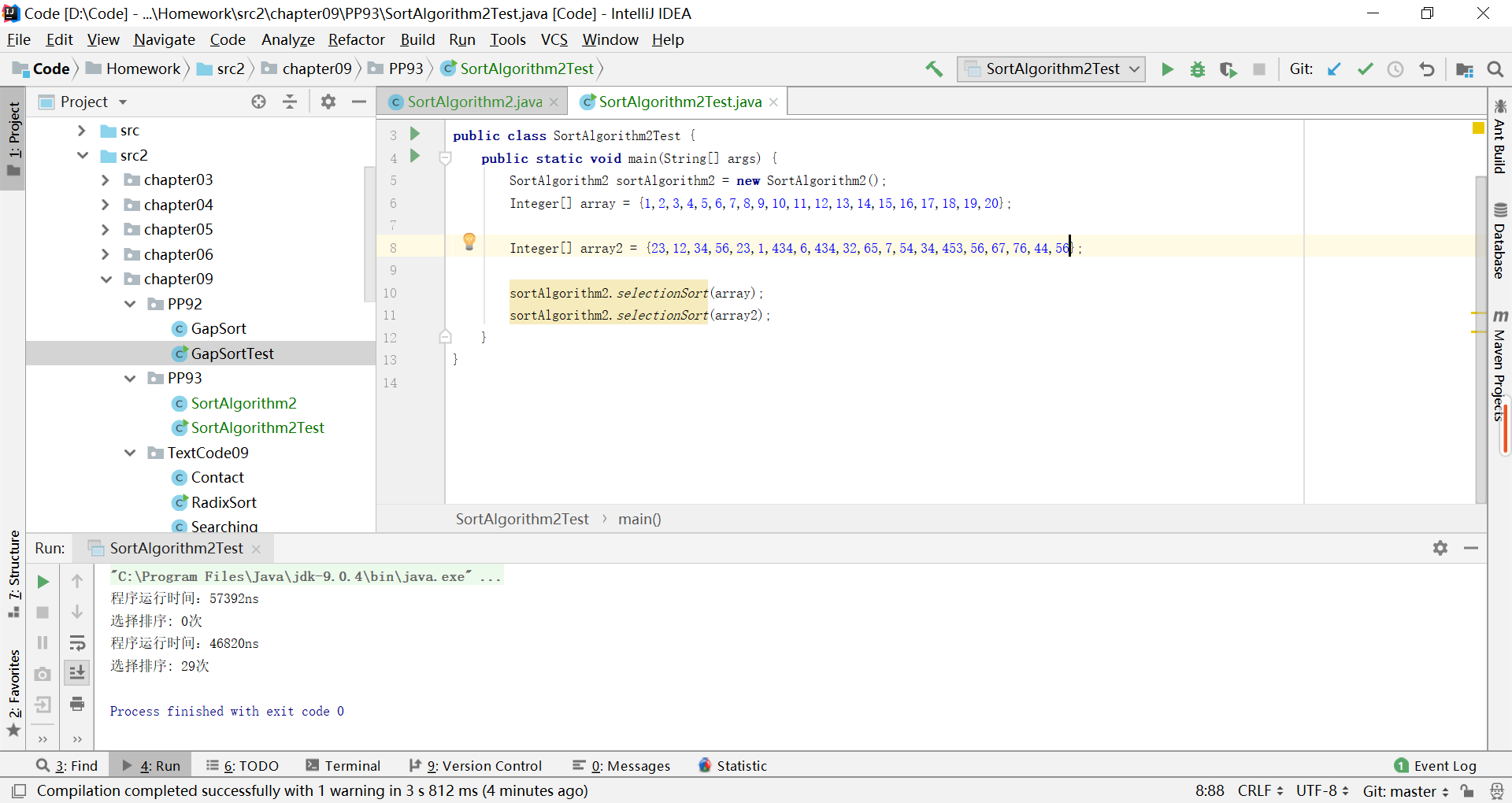
又尝试运行了几十次程序，也有乱序的运行时间长于顺序的情况，但大多数情况还是顺序花费的时间更多

这是跟电脑有关系还是一种巧合，还是其它的什么原因？
暂时并没有百度到相关的解释，等找到了再来补充

还存在一个问题，就是，递归的计数与时间计算好像跟其它排序算法不一样，不能直接一次输出结果，每次调用自己，就会又一次把结果打印一遍，像这样：

所以不能在递归方法里写计算时间差的方法，调用次数还是可以的，设一个全局变量，每次调用都会自增1，即可（但是输出还得写在测试类里）

那时间的话，可以统计开始调用这个方法到结束时计算机的时间，做差
那问题就是如何获得计算机时间（但时间精确度可能不高）
百度的方法有说可以调用这个方法1000次，然后取千分之一，但是经过前面的体验，方法的每一次调用花费的时间跟电脑的性能和状态有很大关系，因此一次计算不是很准确，1000次求平均的话，可能更有代表性，更合理；

【更新】
有百度到可以获取当前精确时间（毫秒）的方法，这样就简单了，代码如下：

Calendar Cld = Calendar.getInstance();
int YY = Cld.get(Calendar.YEAR) ;//年
int MM = Cld.get(Calendar.MONTH)+1;//月
int DD = Cld.get(Calendar.DATE);//日
int HH = Cld.get(Calendar.HOUR_OF_DAY);//时
int mm = Cld.get(Calendar.MINUTE);//分
int SS = Cld.get(Calendar.SECOND);//秒
int MI = Cld.get(Calendar.MILLISECOND);//毫秒    
//由整型而来,因此格式不加0,如  2017/5/5-1:1:32:694
System.out.println(YY + "/" + MM + "/" + DD + "-" + HH + ":" + mm + ":" + SS + ":" + MI);

emmm，好像。。。
通过重新写一个方法来调用这个排序的递归方法，然后在这个方法里面再进行时间统计，就可以避免重复打印多次了，也就不用在测试类里统计时间了，更符合题意，运行结果如图：

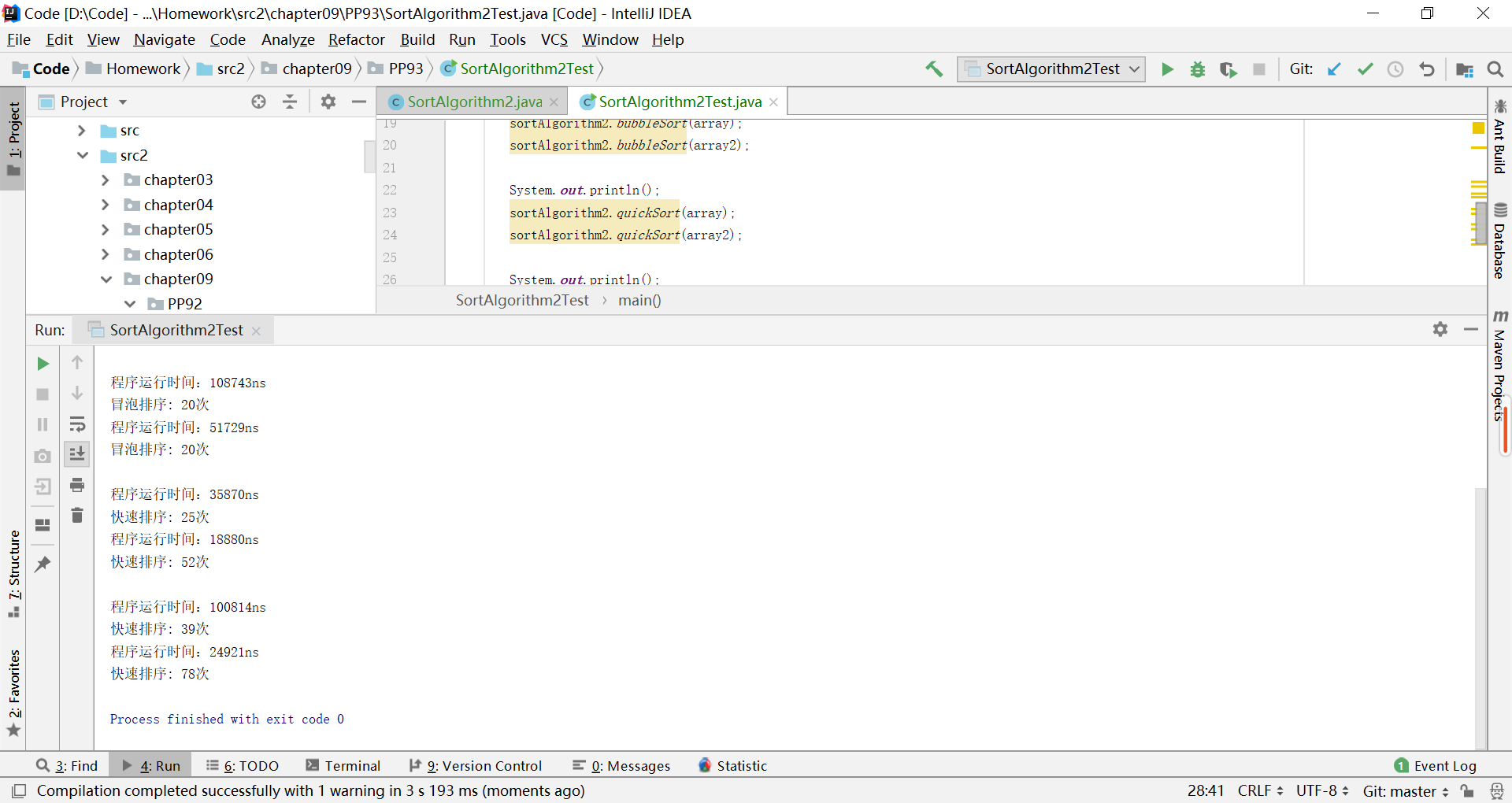
也百度到一些计算递归方法运行的时间，但可能涉及到后面的内容，也没有详细讲，看的不是很明白

【参考资料】
java如何计算程序运行时间
 怎么记录递归函数的使用次数
 解递归算法的运行时间的三种方法

本周错题

无

代码托管

结对及互评

博客中值得学习的或问题：
- 侯泽洋同学的博客排版工整，界面很美观
- 问题总结做得很全面：每一种排序方法都能找到适当的图片描述，说明问题
- 对各种排序的时间复杂度做了总结比较，值得我去学习
- 对教材中的细小问题都能够关注，并且主动去百度学习，例如代码中“@SuppressWarnings("unchecked")”的含义理解
代码中值得学习的或问题：
- 对于编程的编写总能找到角度去解决
本周结对学习情况
- 20172302
- 结对学习内容
  - 第九章内容：排序与查找

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	4/4
第二周	560/560	1/2	6/10
第三周	415/975	1/3	6/16
第四周	1055/2030	1/4	14/30
第五周	1051/3083	1/5	8/38

posted @ 2018-10-15 21:41 20172308周亚杰阅读(432) 评论(3) 编辑收藏举报

刷新页面返回顶部

20172308周亚杰