哈夫曼树实践
关于哈夫曼树
*1. 节点之间的路径长度:在树中从一个结点到另一个结点所经历的分支,构成了这两个结点间的路径上的经过的分支数称为它的路径长度
*2. 树的路径长度:从树的根节点到树中每一结点的路径长度之和。在结点数目相同的二叉树中,完全二叉树的路径长度最短。
*3. 结点的权:在一些应用中,赋予树中结点的一个有某种意义的实数。
*4. 结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积
*5. 树的带权路径长度:定义为树中所有叶子结点的带权路径长度之和
*6. 最优二叉树:从已给出的目标带权结点(单独的结点) 经过一种方式的组合形成一棵树.使树的权值最小.。最优二叉树是带权路径长度最短的二叉树。根据结点的个数,权值的不同,最优二叉树的形状也各不相同。它们的共同点是:带权值的结点都是叶子结点。权值越小的结点,其到根结点的路径越长。
哈夫曼树的实现
哈夫曼树的节点类
public class HuffmanTreeNode implements Comparable<HuffmanTreeNode> {
private int weight;
private HuffmanTreeNode parent, left, right;
private char character;
public HuffmanTreeNode(HuffmanTreeNode parent, HuffmanTreeNode left, HuffmanTreeNode right, int weight, char character) {
this.weight = weight;
this.character = character;
this.parent = parent;
this.left = left;
this.right = right;
}
@Override
public int compareTo(HuffmanTreeNode huffmanTreeNode) {
return this.weight - huffmanTreeNode.getWeight();
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public HuffmanTreeNode getParent() {
return parent;
}
public void setParent(HuffmanTreeNode parent) {
this.parent = parent;
}
public HuffmanTreeNode getLeft() {
return left;
}
public void setLeft(HuffmanTreeNode left) {
this.left = left;
}
public HuffmanTreeNode getRight() {
return right;
}
public void setRight(HuffmanTreeNode right) {
this.right = right;
}
public char getCharacter() {
return character;
}
public void setElement(char character) {
this.character = character;
}
}
哈夫曼树的构造
构造哈夫曼树是最重要的一步,因为它关系到编码的0/1序号是否正确以及简单
课堂上对于哈夫曼树的理解不是很明白,通过这篇博客有了更深的了解哈夫曼树(三)之 Java详解
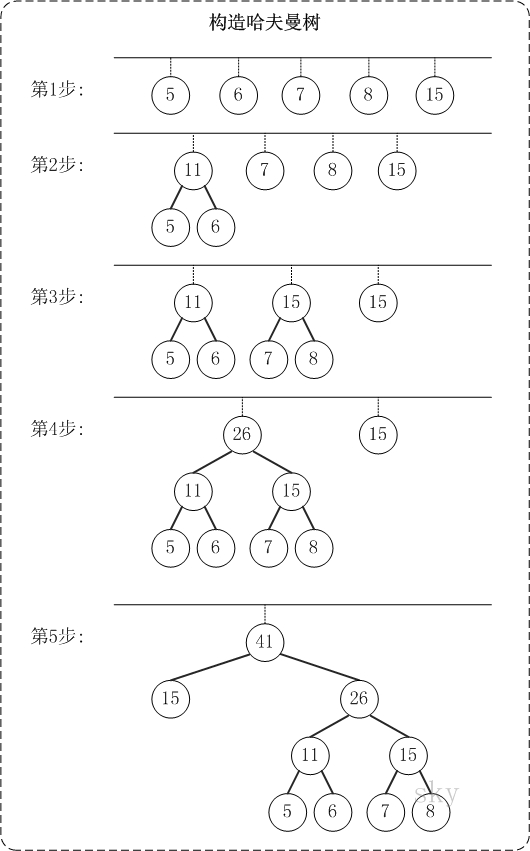
有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,哈夫曼树的构造规则为:
- 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
- 在森林中选出根结点的权值最小的两棵树进行合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
- 从森林中删除选取的两棵树,并将新树加入森林;
- 重复(02)、(03)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树
构造哈夫曼树需要对权值进行排序,每次取出两个最小值并求和作为父节点组成一颗小树,如此重复直至只剩一棵树即为所求哈夫曼树
排序有多种方法,这里用的是堆排序:
按顺序每次取两个最小值,第一个作为左孩子(编码为0),第二个作为右孩子(编码为1)
然后求和,将其设为父节点
继续循环
具体过程如图所示:
以{5,6,7,8,15}为例,来构造一棵哈夫曼树:
public class HuffmanTree
{
private HuffmanTreeNode mRoot; // 根结点
private String[] codes = new String[26];//用数组存放26个字母的概率(即权值)
public HuffmanTree(HuffmanTreeNode[] array) {
HuffmanTreeNode parent = null;
ArrayHeap<HuffmanTreeNode> heap = new ArrayHeap();
for (int i=0;i<array.length;i++)
{
heap.addElement(array[i]);//将权值放入堆中
}
for(int i=0; i<array.length-1; i++) {
HuffmanTreeNode left = heap.removeMin(); //取第一个 最小节点作为左孩子
HuffmanTreeNode right = heap.removeMin();//取第二个 最小节点作为右孩子
parent = new HuffmanTreeNode(null,left,right,left.getWeight()+right.getWeight(),' ');//求左右孩子之和并存为哈夫曼节点
left.setParent(parent);
right.setParent(parent);//将和设置为左右孩子的父节点
heap.addElement(parent);//将父节点添加到新的堆中(此时两个孩子已经被删除)
}
mRoot = parent;//循环结束,把最后一个父节点设置为根结点
}
}
哈夫曼编码
根据前面所说的哈夫曼编码规则
哈夫曼树的左孩子对应0,右孩子对应1
所以只要能判断根结点到叶子节点路径上的所有节点是左还是右孩子即可写出对应编码
但是存在的问题就是,此那个根节点开始写还是从叶子节点写
因为最终的编码是从根结点开始写起的,但是从根节点开始写就无法判断哪条路径是通向叶子节点,判断会很麻烦
所以只要先将所有的叶子节点找出来存在数组里,然后向上去找
通过
if (node==node.getParent().getLeft())
stack.push(0);
if (node==node.getParent().getRight())
stack.push(1);
来判断当前节点是左孩子还是右孩子
然后输出栈里的0/1,即为正序的编码
public String[] getEncoding() {
ArrayList<HuffmanTreeNode> arrayList = new ArrayList();
inOrder(mRoot,arrayList);//将叶子节点中序遍历存放在列表里
for (int i=0;i<arrayList.size();i++)
{
HuffmanTreeNode node = arrayList.get(i);//将每一个列表中元素变成哈夫曼节点
String result ="";
int x = node.getCharacter()-'a';//x为列表中元素转化为字母表中顺序的索引值
Stack stack = new Stack();//每一次栈里存放的都是某一个元素的编码值的逆序
while (node!=mRoot)//判断当前节点是左孩子还是右孩子
{
if (node==node.getParent().getLeft())
stack.push(0);
if (node==node.getParent().getRight())
stack.push(1);
node=node.getParent();//判断完当前节点后,节点向上移动
}
while (!stack.isEmpty())
{
result +=stack.pop();
}
codes[x] = result;//result为每一个字母的哈夫曼编码值,存放在对应的字母索引值x处
}
return codes;//codes为存放每一个字母编码值的数组
}
哈夫曼解码
因为哈夫曼编码是变长的,也就是每一个元素对应的0/1个数不一样长,无法判断哪几位对应哪一个元素
但是根据哈夫曼树原理,仍然可以通过一个一个的读取0/1来进行判断,因为一个0/1就对应了当前节点是左还是右孩子
每读取一次,就判断当前节点有无孩子,而只要读取到叶子节点,即找到了一个字母元素
//从文件读取
Scanner scan1 = new Scanner(file1);
String string = scan1.nextLine();//string为原文编码后的所有内容
HuffmanTreeNode huffmanTreeNode = huffmanTree.getmRoot();//从根节点开始读取
//进行解码
String result2 = "";
for (int i = 0; i < string.length(); i++) {
if (string .charAt(i) == '0') {//读取第一个数字判断是否为0(即是否为左孩子)
if (huffmanTreeNode.getLeft() != null) {//判断当前节点是否有左孩子
huffmanTreeNode = huffmanTreeNode.getLeft();
}
} else {
if (string .charAt(i) == '1') {
if (huffmanTreeNode.getRight() != null) {
huffmanTreeNode = huffmanTreeNode.getRight();
}
}
}
if (huffmanTreeNode.getLeft() == null && huffmanTreeNode.getRight() == null) {//判断当前节点是否为叶子节点
result2 += huffmanTreeNode.getCharacter();//是叶子节点即为找到了一个字母,将其加入到解码后的结果result2
huffmanTreeNode = huffmanTree.getmRoot();//找到一个字母,即从根结点开始继续循环找下一个字母
}//如果一次循环没找到,则继续循环直到找到叶子节点,数字读完即为循环结束
}
文章中字母出现的概率统计
侯泽洋同学统计字母出现概率的方法非常好!
从中受益匪浅
他直接将每个字母减掉‘ a ’,对应ASCII表中的差值即为当前字母对应26个字母中的位置索引
从而每一个差值相等的字母都是相同的,且能知道这个字母是谁
Scanner scan = new Scanner(file);
String s = scan.nextLine();
int[] array = new int[26];
for (int i = 0; i < array.length; i++) {
array[i] = 0;//初始化
}
for (int i = 0; i < s.length(); i++) {
char x = Character.toLowerCase(s.charAt(i));//将大写字母转换成小写字母
array[x - 'a']++;//相同字母的位置索引上的数字自增
}
System.out.println("打印各字母出现频率:");
for (int i = 0; i < array.length; i++) {
System.out.println((char)('a'+i)+":"+(double) array[i] / s.length());
}

