20172308 实验三《程序设计与数据结构》查找与排序 实验报告

20172308 2018-2019-1 实验3 《查找与排序》报告

课程：《程序设计与数据结构》
班级： 1723
姓名： 周亚杰
学号：20172308
实验教师：王志强
实验日期：2018年10月20日
必修/选修： 必修

1.实验内容

• 查找与排序-1：定义一个Searching和Sorting类，并在类中实现linearSearch, SelectionSort方法
• 查找与排序-2：重构代码
• 查找与排序-3：参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试
• 查找与排序-4：补充实现课上讲过的排序方法
• 查找与排序-5：编写Android程序对各种查找与排序算法进行测试

2. 实验过程及结果

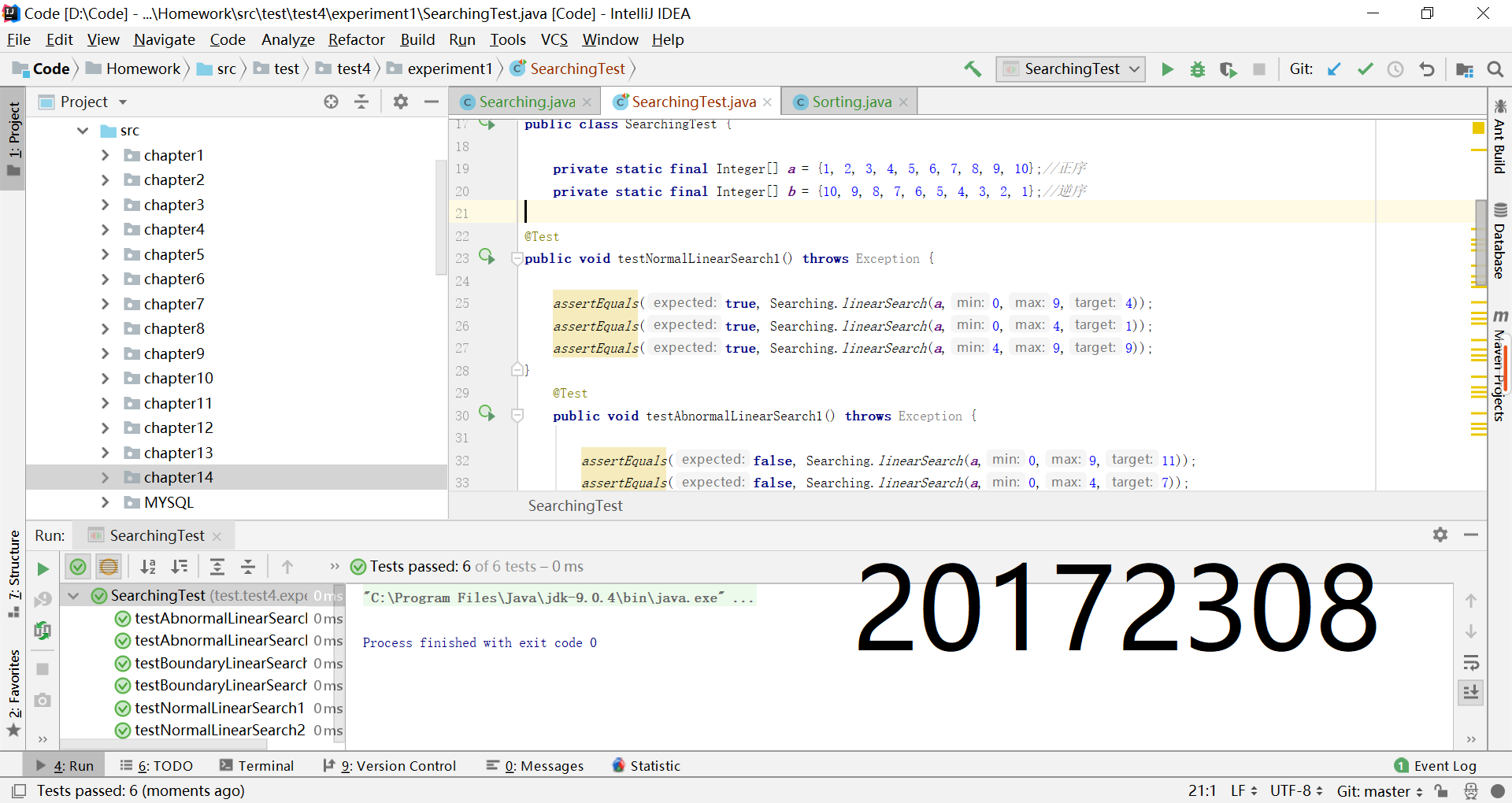
• 查找与排序-1：

1. 定义一个Searching和Sorting类
2. 在类中实现linearSearch, SelectionSort方法
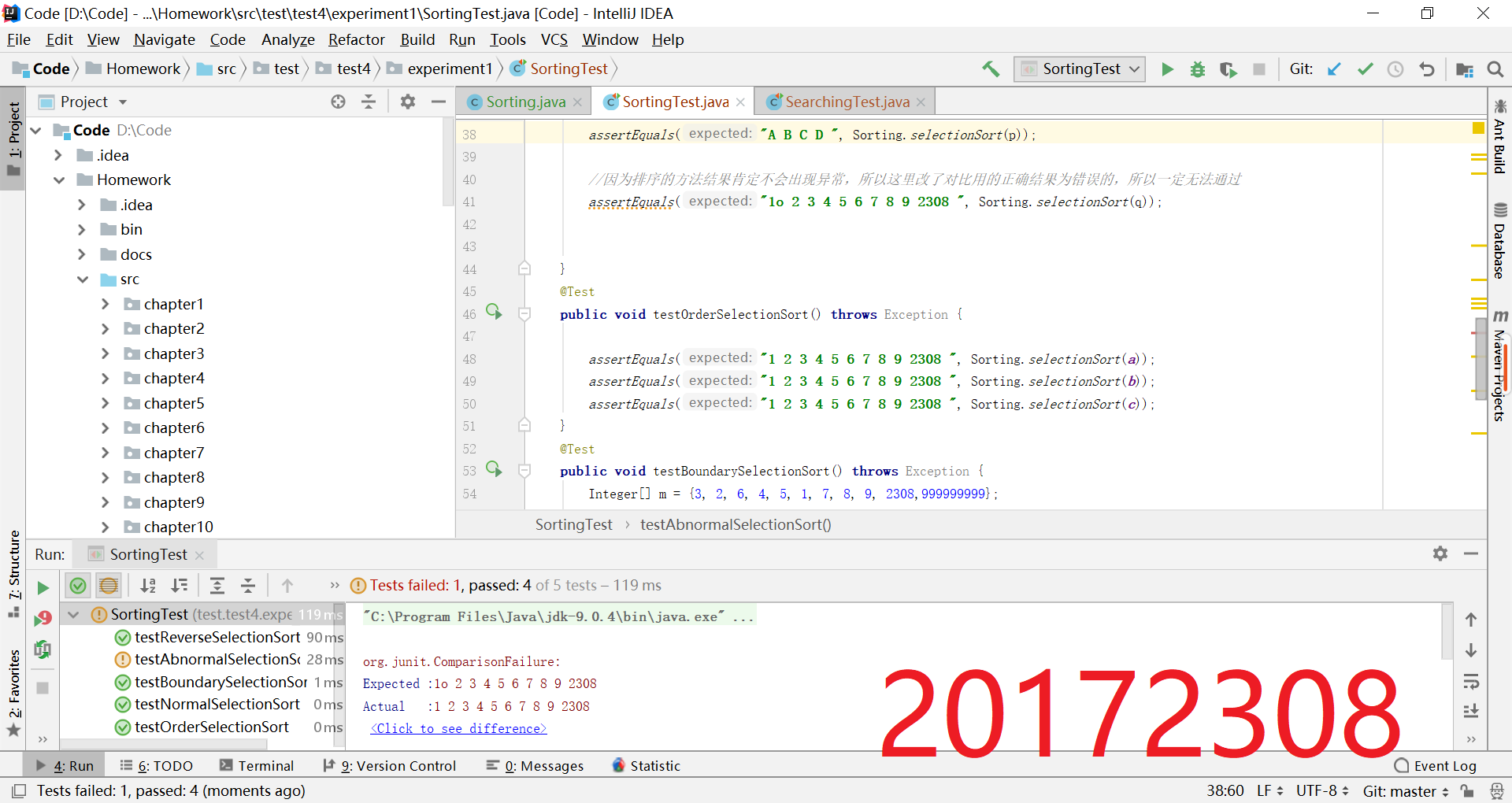
3. 10个测试用例，提交测试用例设计情况（正常，异常，边界，正序，逆序），用例数据中要包含自己学号的后四位
4. 测试用例的选取要考虑到方法的形参，设计选取的用例
5. 完成测试
6. 结果截图：
   

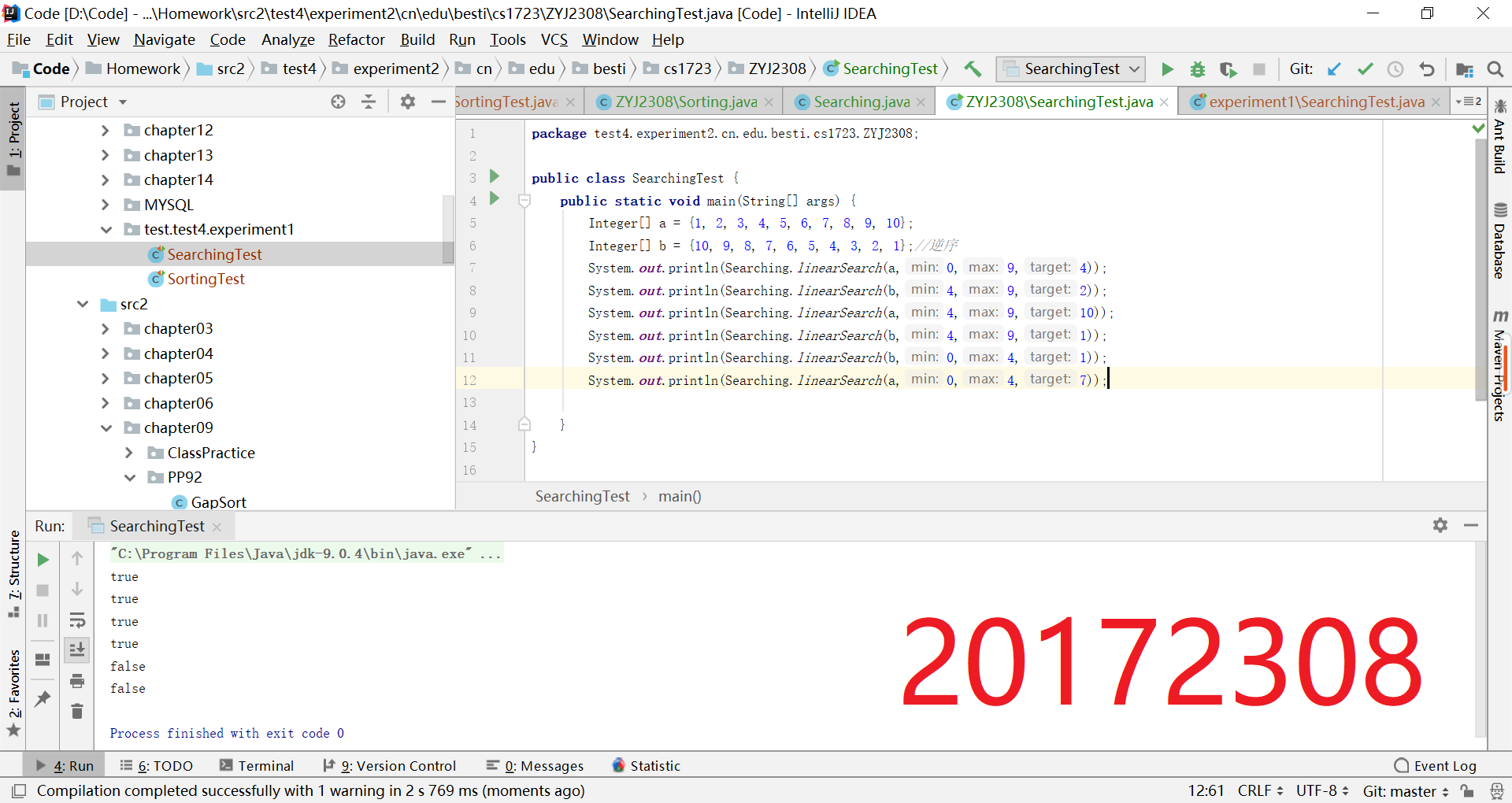
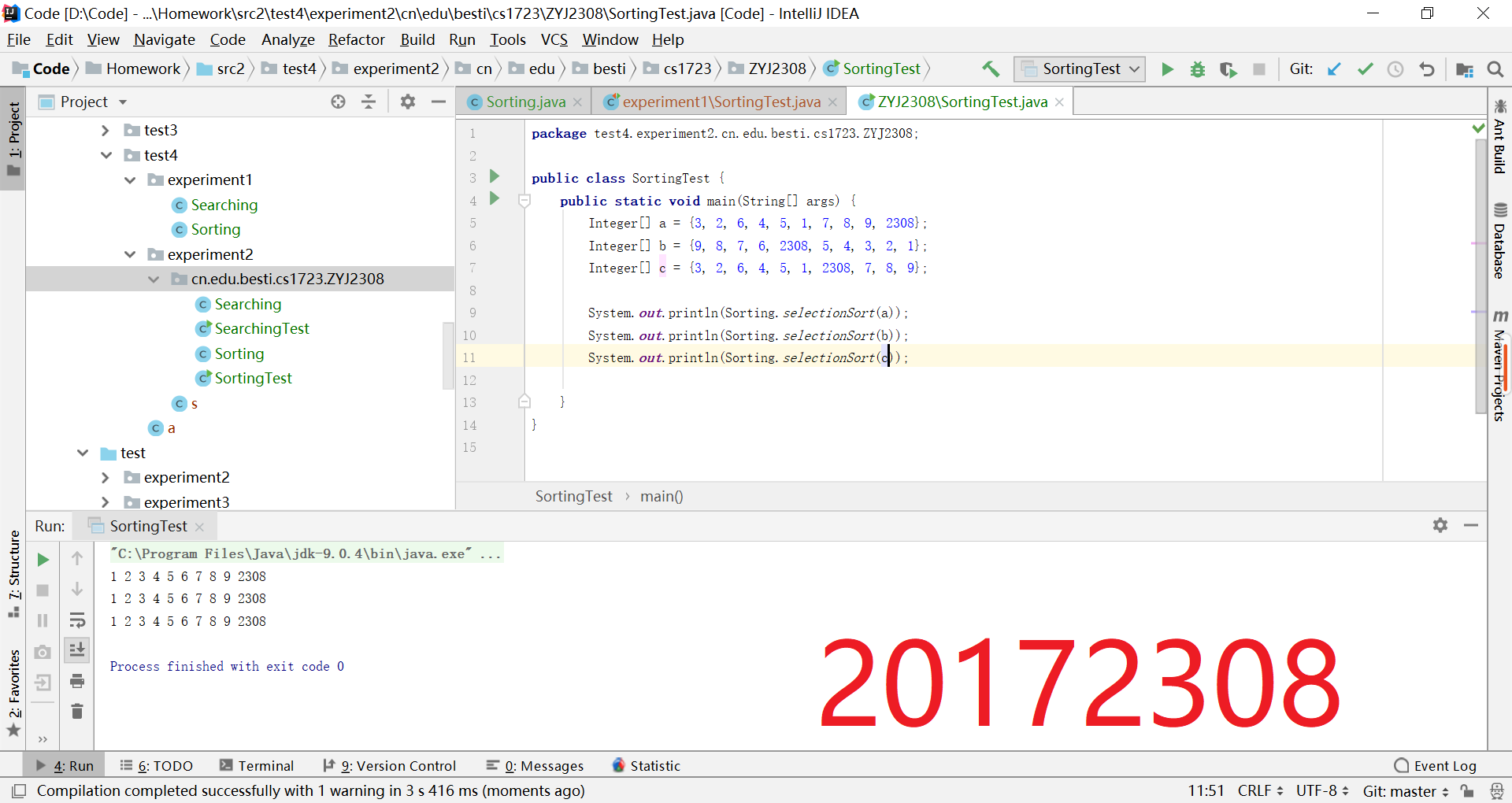
• 查找与排序-2：

1. 重构代码
2. 把Sorting.java Searching.java放入 cn.edu.besti.cs1723.（姓名首字母+四位学号）包中
3. 把测试代码放test包中
4. 重新编译，运行代码，提交编译，运行的截图（IDEA，命令行两种）
5. 结果截图
   
   

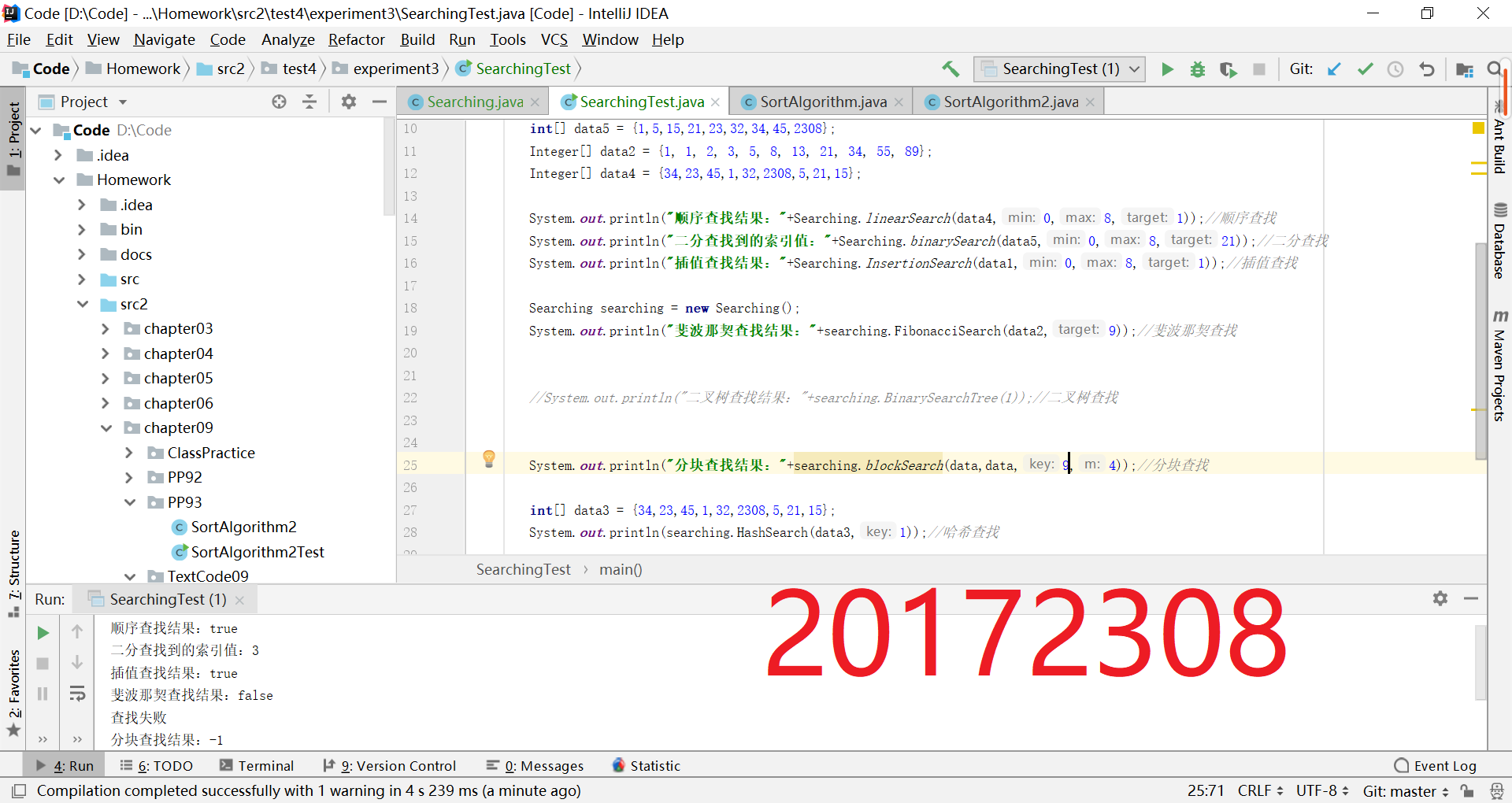
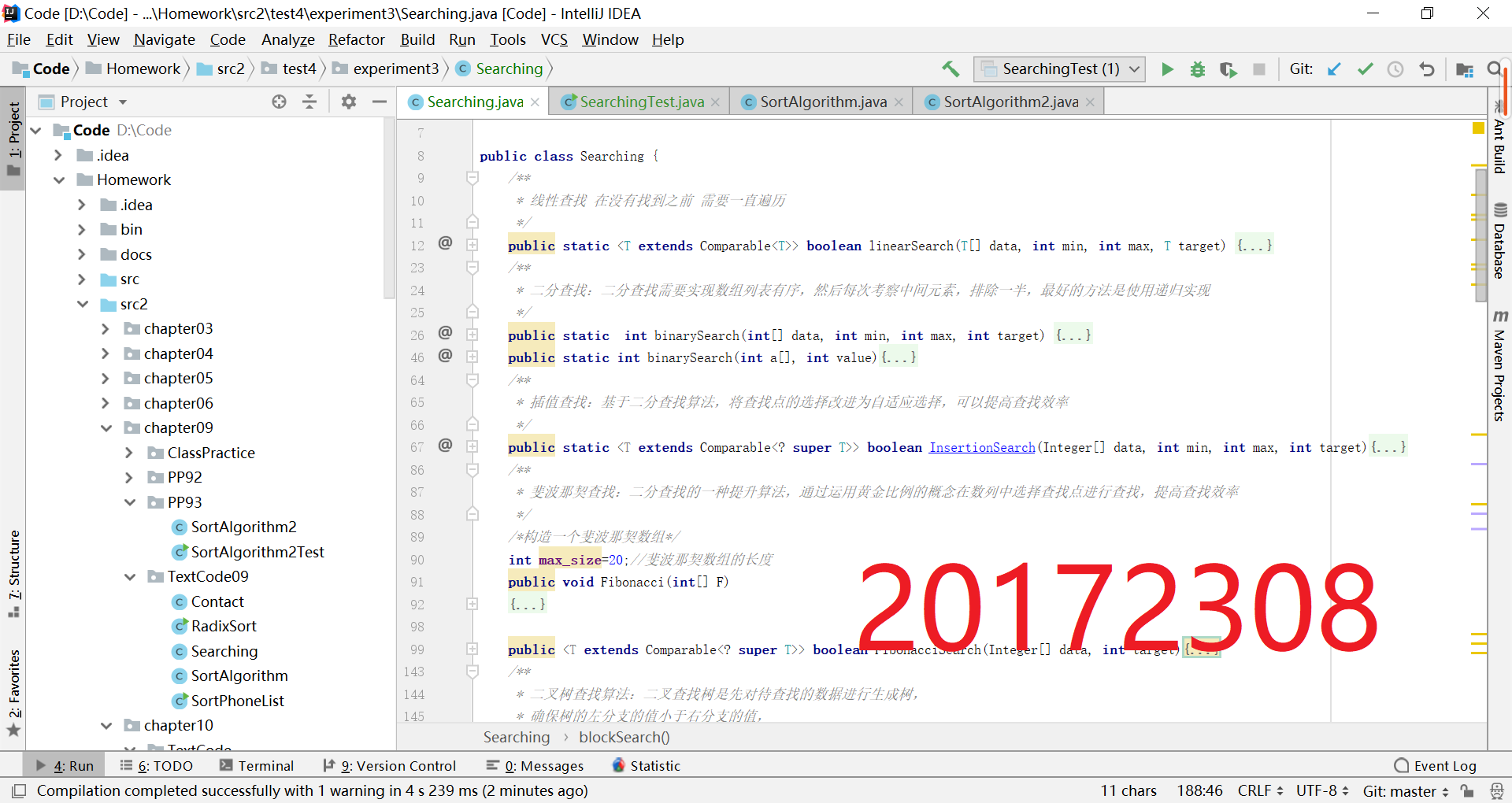
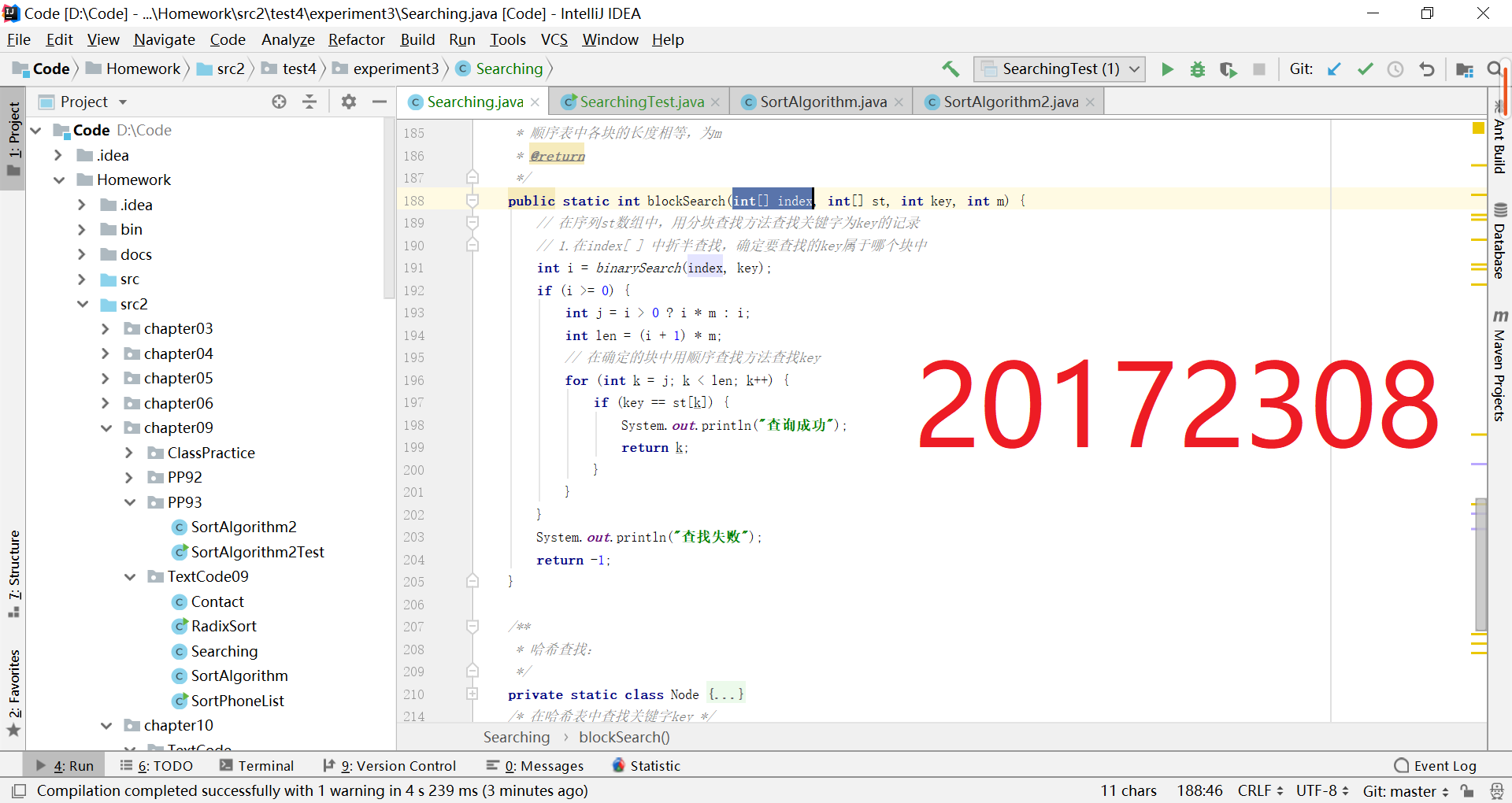
• 查找与排序-3：

1. 参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试
2. 根据参考博客给的C++代码，用Java完成方法的编写
3. 提交运行结果截图
   
   
   
   
   

• 查找与排序-4：

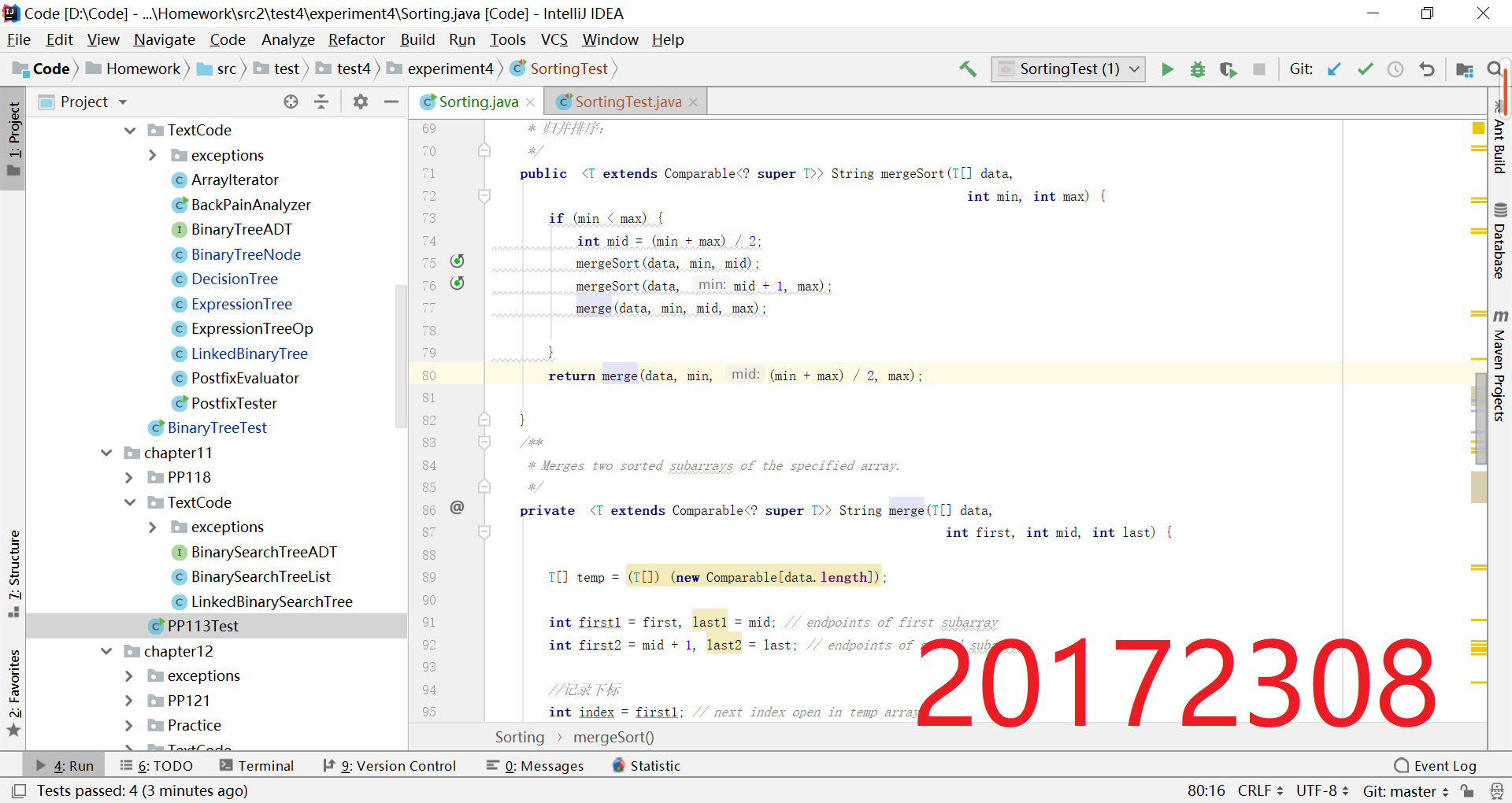
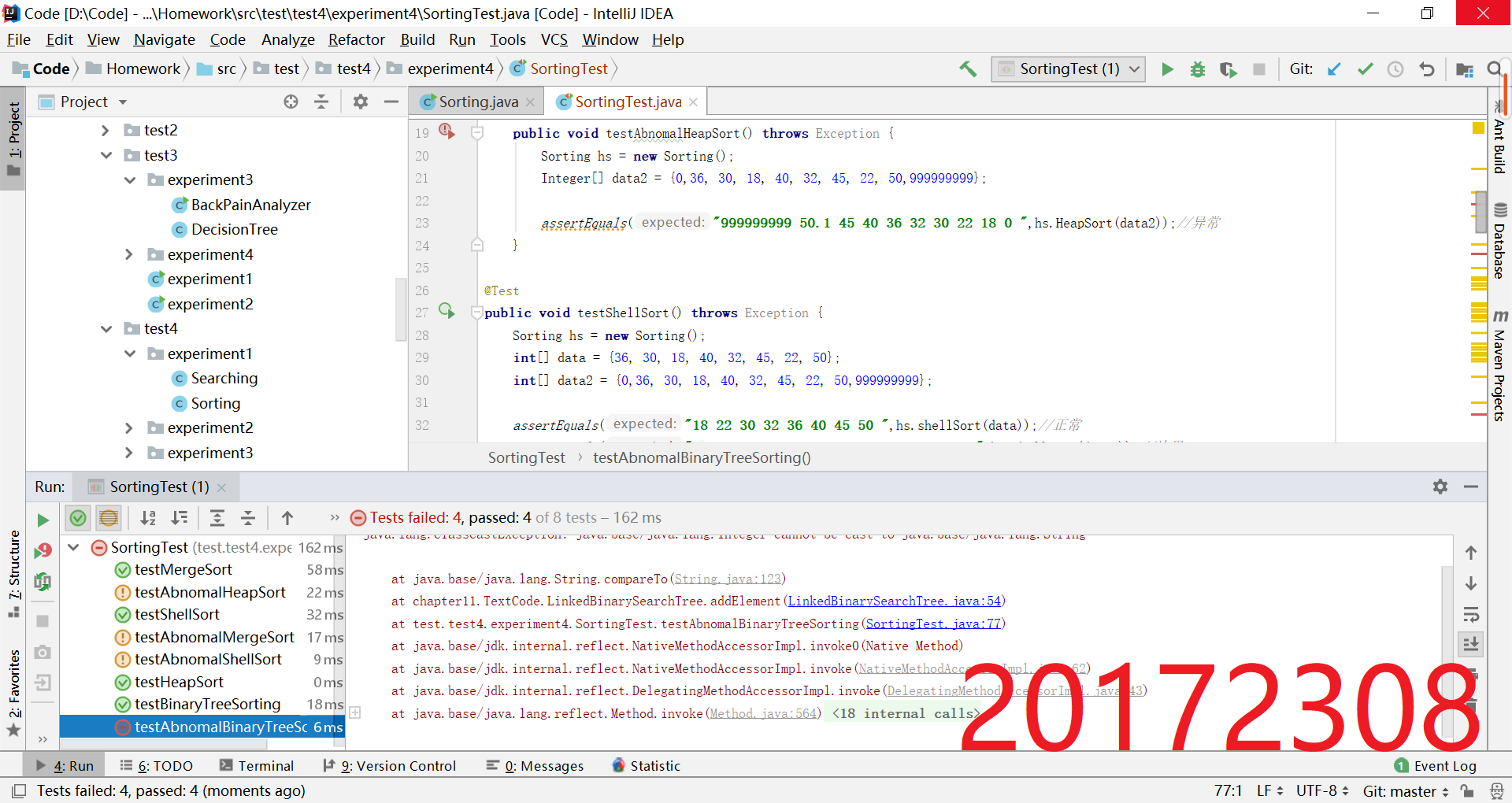
1. 补充实现课上讲过的排序方法：希尔排序，堆排序，二叉树排序等(至少3个)
2. 测试实现的算法（正常，异常，边界）
3. 提交运行结果截图
   

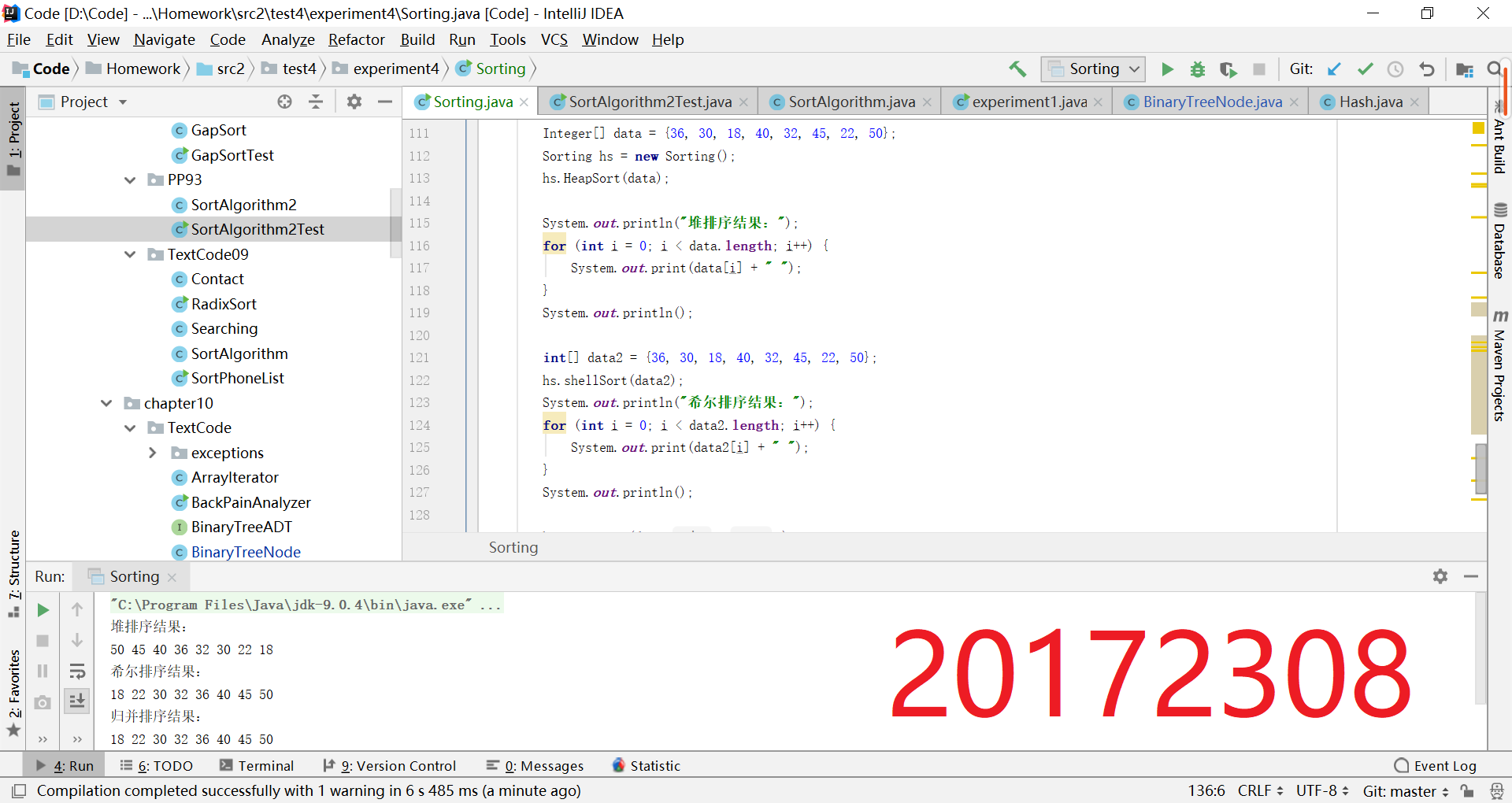
• 查找与排序-5：

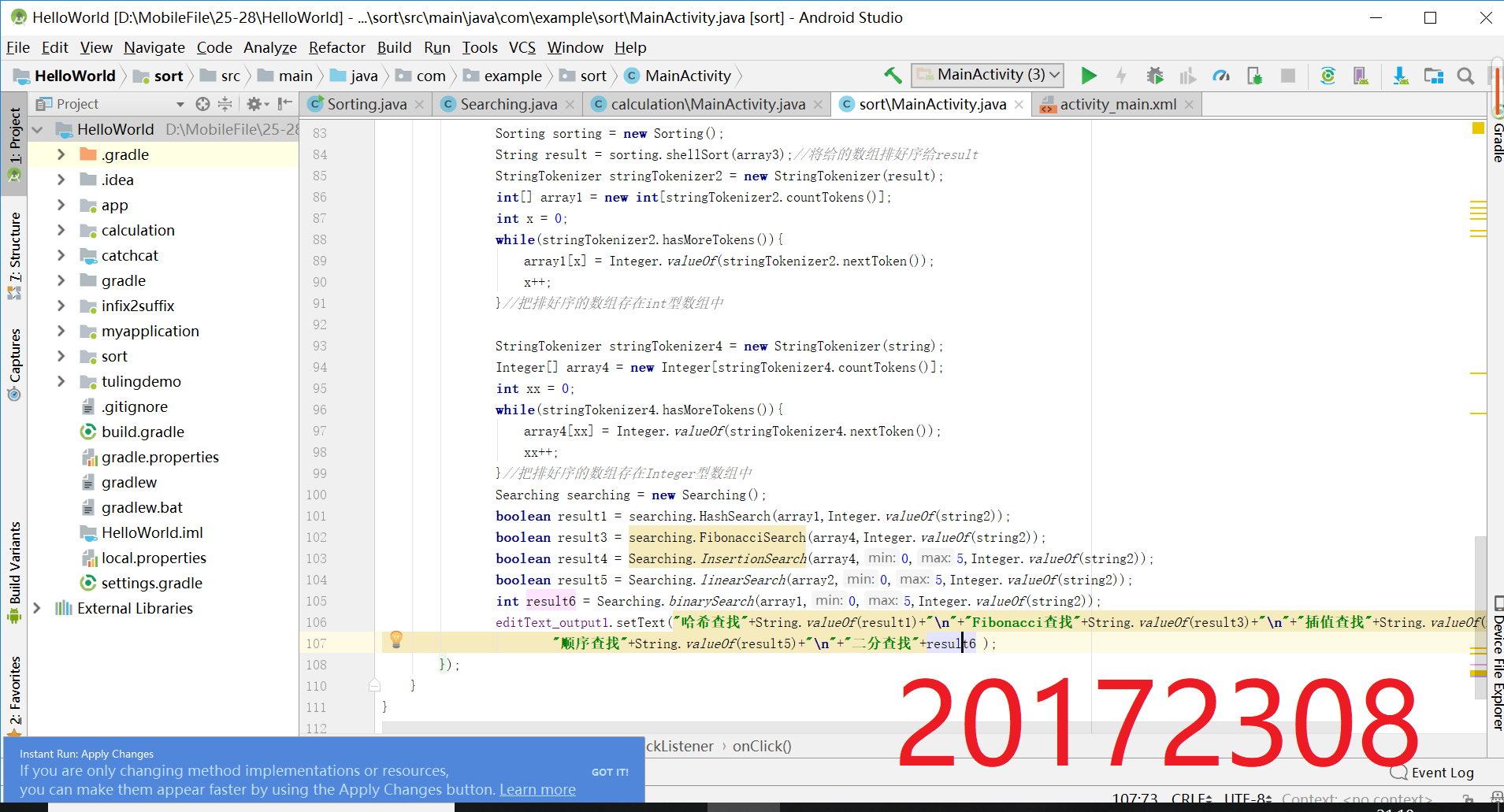
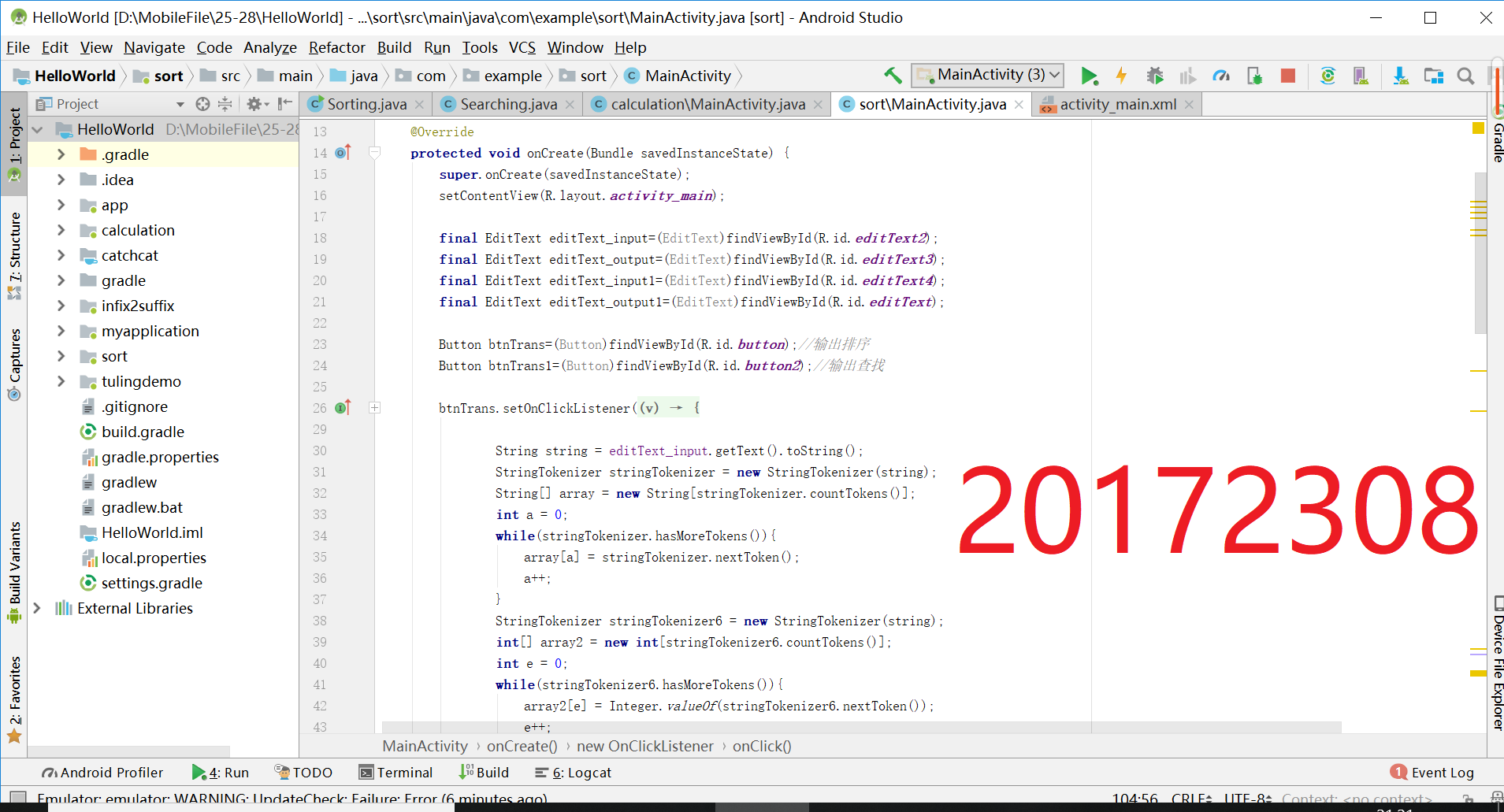
1. 编写Android程序对各种查找与排序算法进行测试
2. 将方法类文件复制到Android studio中
3. 根据需求设计界面，使能够输入数据，返回排序结果；输入查找值，返回true或false
4. 提交运行结果截图
   

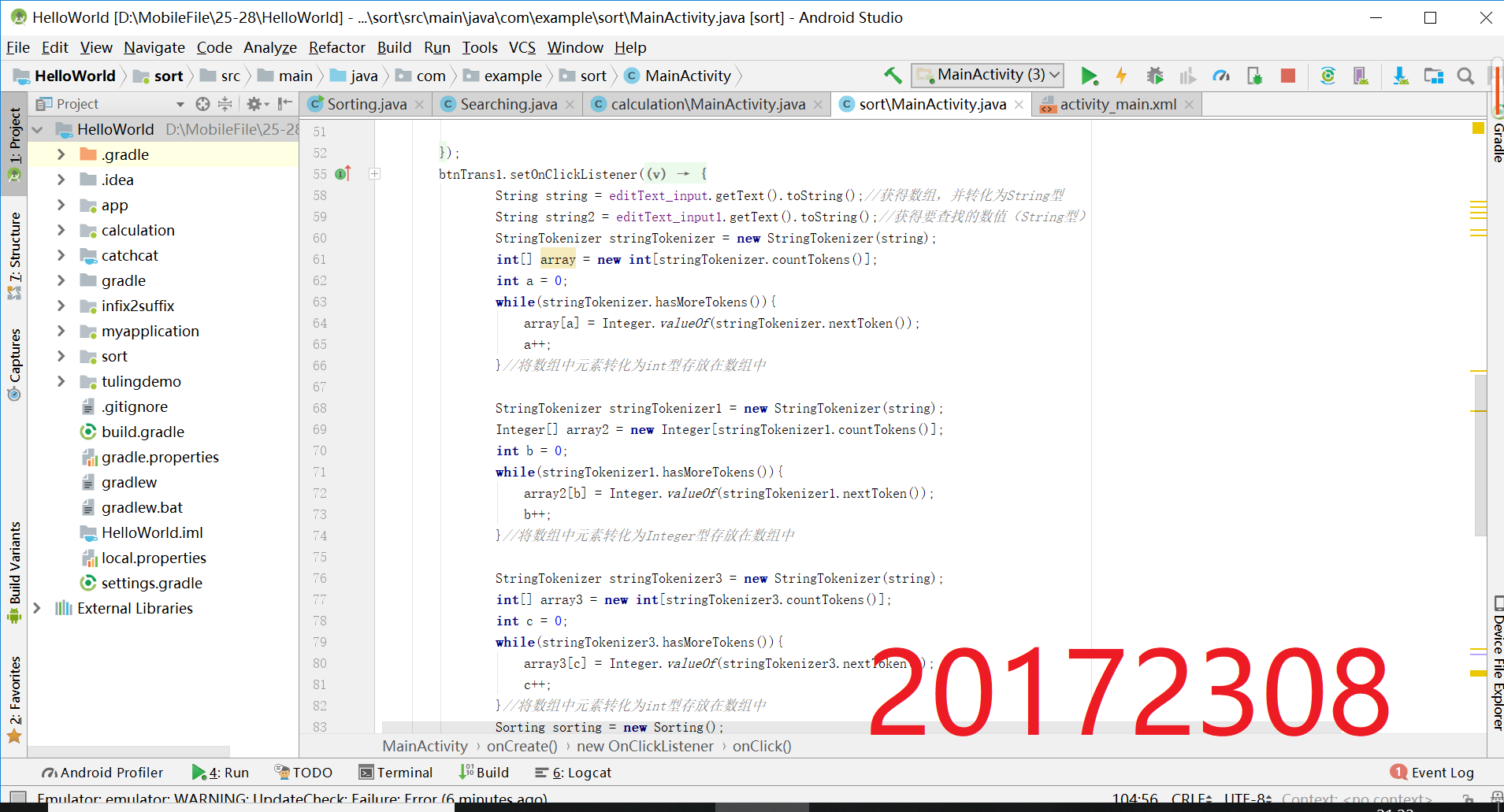
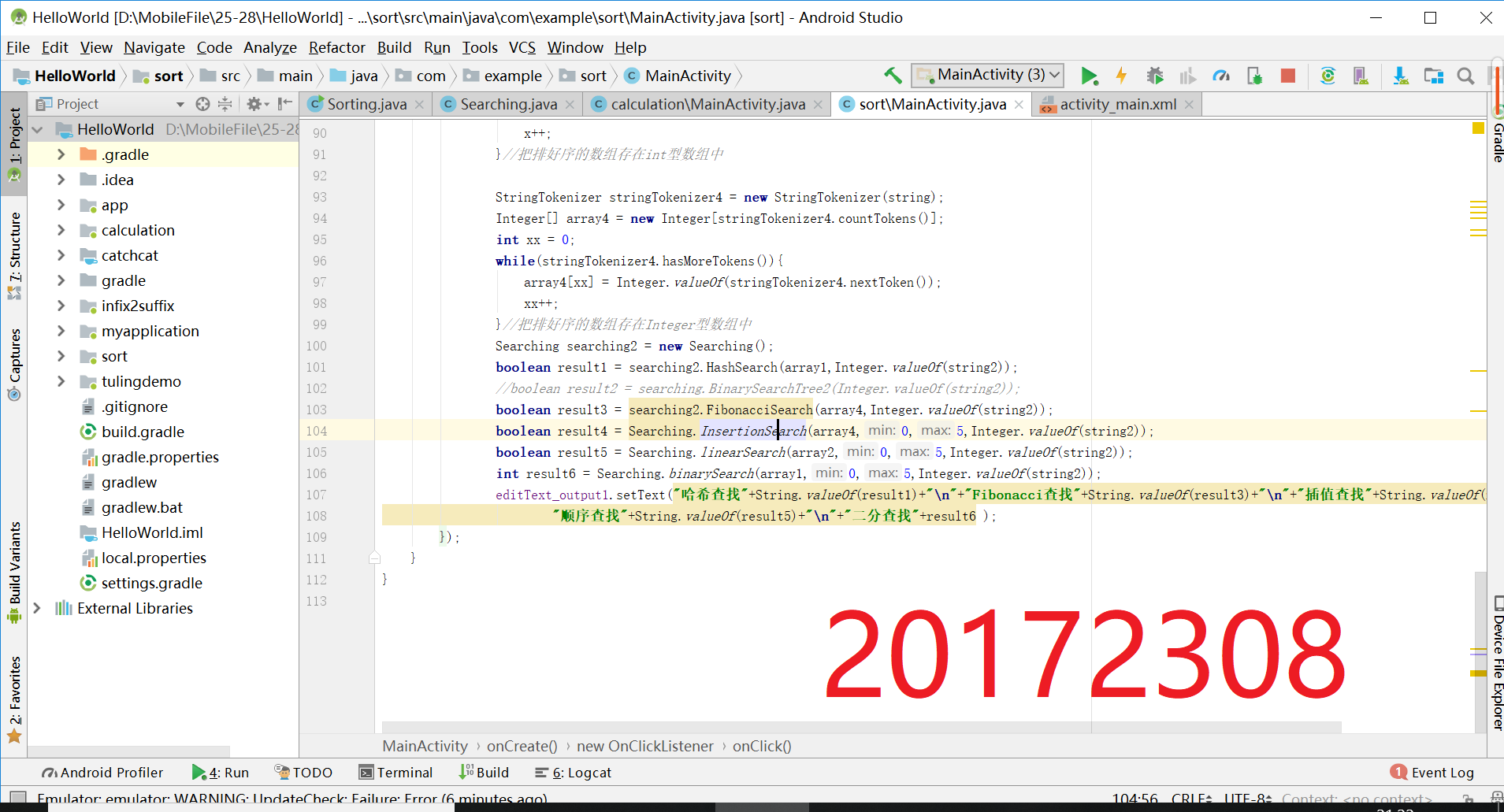
3. 实验过程中遇到的问题和解决过程

• 问题1：实验3是根据参考博客里的内容完成查找方法的编写，比如没有学过的斐波那契查找方法，但是博客里只给了C++的代码，在理解意思之后用Java写出来。
  在写二分查找代码的时候，查找的结果出现了问题：如图
  

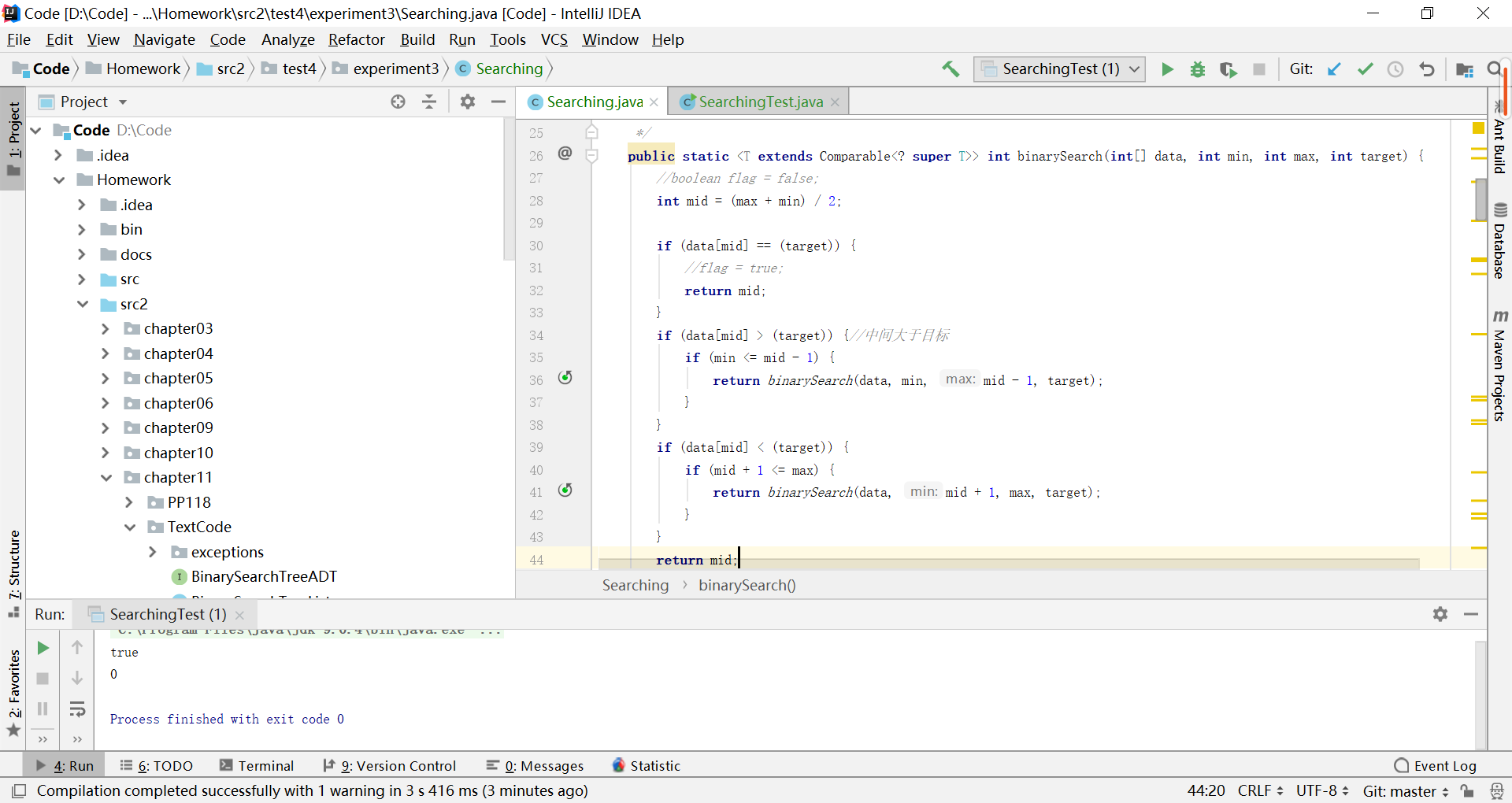
• 问题1解决过程：
  （图中的运行结果是不对的，但是代码是修改之后的）
  测试运行的结果是输出了0，这个很奇怪，输出的应该是我要查找的数字才对
  然后对比参考博客里给的C++代码：

//二分查找（折半查找），版本1
int BinarySearch1(int a[], int value, int n)
{
    int low, high, mid;
    low = 0;
    high = n-1;
    while(low<=high)
    {
        mid = (low+high)/2;
        if(a[mid]==value)
            return mid;
        if(a[mid]>value)
            high = mid-1;
        if(a[mid]<value)
            low = mid+1;
    }
    return -1;
}

//二分查找，递归版本
int BinarySearch2(int a[], int value, int low, int high)
{
    int mid = low+(high-low)/2;
    if(a[mid]==value)
        return mid;
    if(a[mid]>value)
        return BinarySearch2(a, value, low, mid-1);
    if(a[mid]<value)
        return BinarySearch2(a, value, mid+1, high);
}

我用的是递归方法
二分查找是在有序的基础上进行查找的：
参考博客给的方法需要传进去查找的范围，所以在找中间值的时候需要把下限加上
然后判断中间值与要查的值大小关系
若正好相等，直接返回要查值的索引位置
若不相等，则对中间值加减1，然后到新的折半区域求新的中间值，判断相等关系
......
如此递归下去

debug之后，发现问题所在：参考博客里的代码有点问题
方法是类似于上面所说的，但是每一次递归都缺少一次判断：
即每一次递归，新的索引中间值都会增或减1，即缺少判断中间值到达边界的条件
如果要查找的值并不存在，则查到边界的时候，就会越界

在博客的评论里也有人回复了

加上条件之后即可

插值算法与二分查找类似，存在一样的问题
代码如下：

//插值查找
int InsertionSearch(int a[], int value, int low, int high)
{
    int mid = low+(value-a[low])/(a[high]-a[low])*(high-low);
    if(a[mid]==value)
        return mid;
    if(a[mid]>value)
        return InsertionSearch(a, value, low, mid-1);
    if(a[mid]<value)
        return InsertionSearch(a, value, mid+1, high);
}

插值查找不再是一半一半的查找，而是根据所给查找的长度大小来分割查找的区域

修改后的代码如下：

public static boolean InsertionSearch(Integer[] data, int min, int max, int target){
        boolean flag= false;
        int mid = min+(target-data[min])/(data[max]-data[min])*(max-min);

        if (mid <= max || mid >= min) {
            if (data[mid] == (target)) {
                flag = true;
            } else if (data[mid] > (target)) {//中间大于目标
                if (min <= mid - 1) {
                    flag = InsertionSearch(data, min, mid - 1, target);
                }
            } else if (data[mid] < target) {
                if (mid + 1 <= max) {
                    flag = InsertionSearch(data, mid + 1, max, target);
                }
            }
        }
        return flag;
    }

即也加入一行判断，保证mid不会越界
这个也有人评论了

• 问题2：实验2的代码重构，要求用命令行运行程序，很久没有用Linux，已经忘得差不多了

• 问题2解决过程：
  这个问题在实践截止前也没能解决，因为虚拟机的问题没有在Ubuntu上测试运行
  于是在IDEA的命令行上试了很久，百度了很多参考博客，结果都没能成功
  后来试了一下基本命令，如新建文件，ls等结果是——找不到命令（手动脸黑）
  这真是一个悲伤的故事
  百度了一下，应该跟IDEA的命令行相关配置有关

• 问题3：在Android studio里实现前四个实验的功能，其间遇到了小问题

• 问题3解决过程：
  第一个是将文件复制到Android studio里面时，原先文件里的import引用到这里不能用了，因为AS里已经有一些包结构了
  但是手动改的话会累死人的，因为这些查找用到了许多本书前几章的代码，懒得找，，，索性将所有文件都拷过去，所以说一个一个文件的改不现实
  所以根据包名，将这几个实验的代码放进相应的包里即可

4.感悟

本次实验让我意识到学过的只是应当多用多回顾，比如说Linux，Android studio，而不能学过就算了