排序算法

冒泡排序

1.动图演示

2.代码实现

private static void bubbleSort(int[] arr) {
    if (arr.length <= 1) return;
    for (int i = 0; i < arr.length; i++) {
        // 用于标识数组是否有序
        boolean order = true;
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                order = false;
            }
        }
        if (order) break;
    }
}

选择排序

1.动图演示

2.代码实现

private static void selectionSort(int[] arr) {
    if (arr.length <= 1) return;
    for (int i = 0; i < arr.length - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

插入排序

1.动图演示

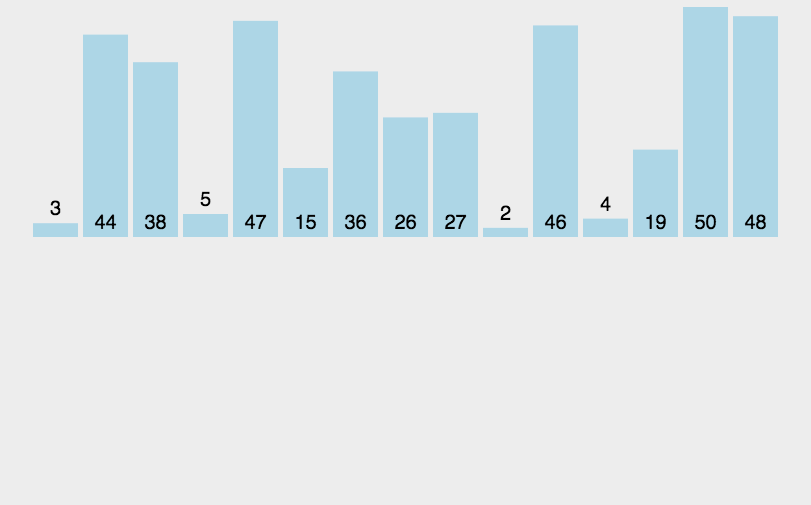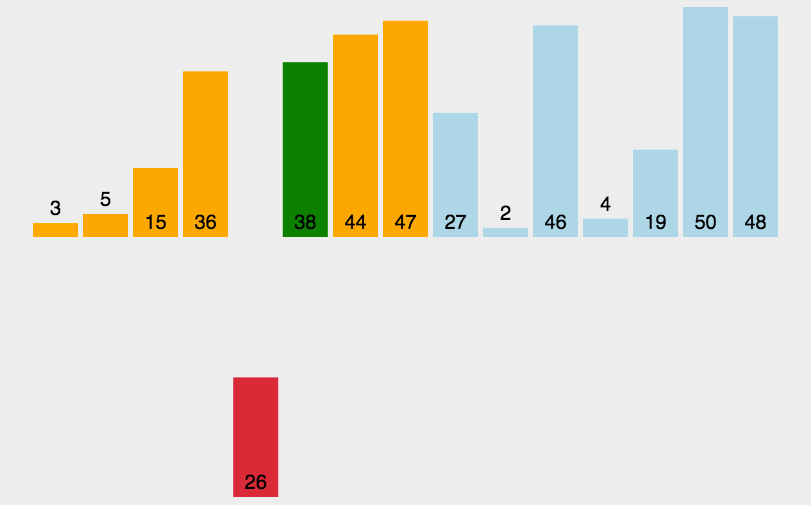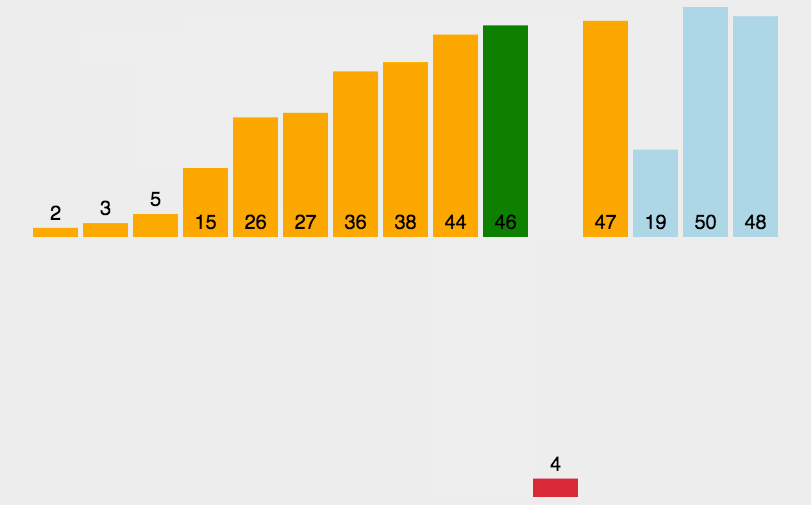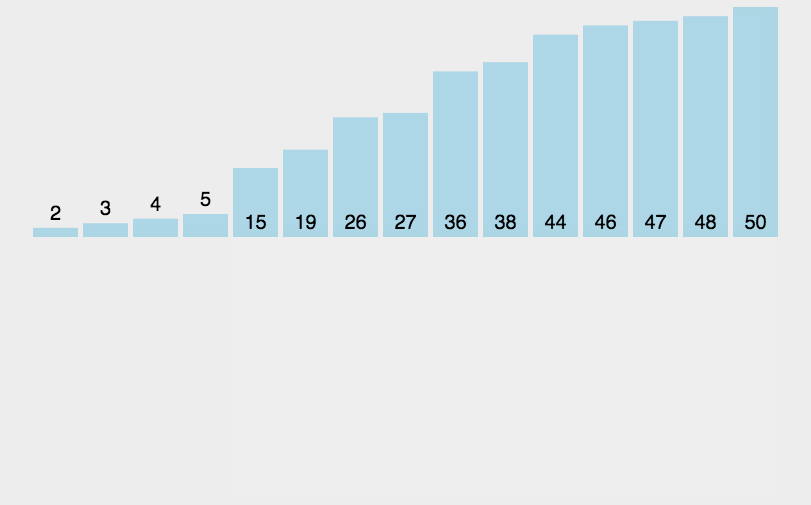
2.代码实现

private static void insertionSort(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int current = arr[i];
        int preIndex = i - 1;
        // 被比较的数大于上一个，上一个的下标就往前一个
        while (preIndex >= 0 && current < arr[preIndex]) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
}

希尔排序

1.动图演示

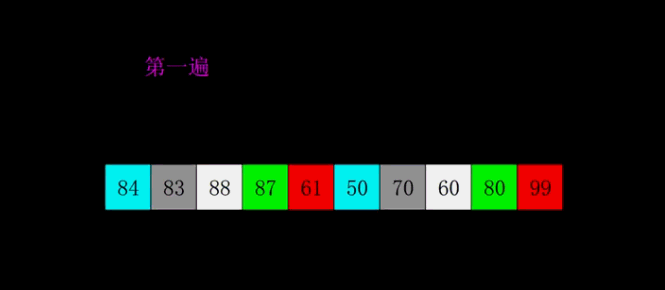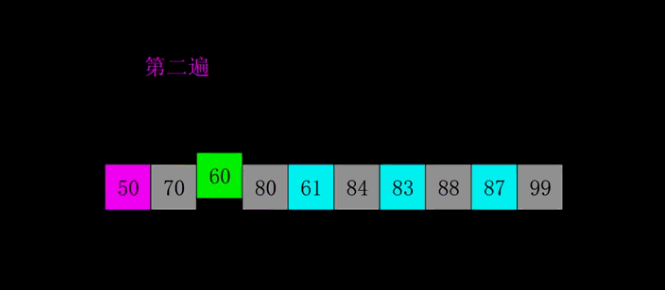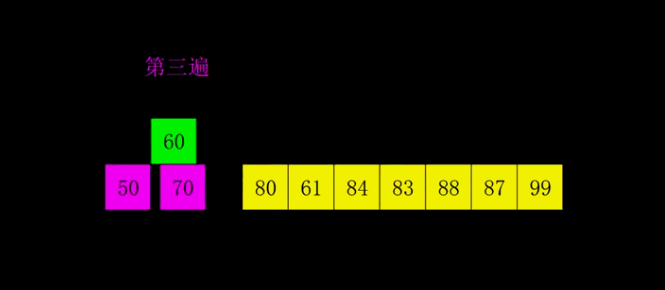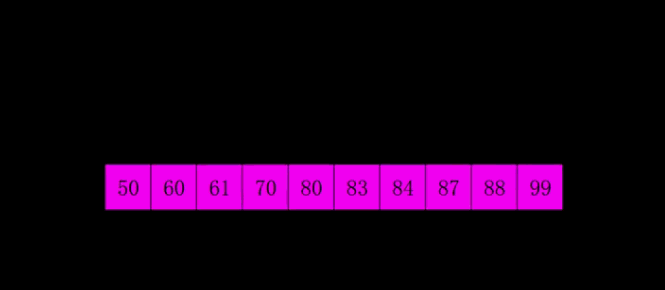
2.代码实现

private static void shellSort(int[] arr) {
    for (int gap = arr.length/2; gap > 0 ; gap = gap/2) {
        for (int i = gap; i < arr.length; i++) {
            int current = arr[i];
            int preIndex = i - gap;
            if (preIndex >= 0 && current < arr[preIndex]) {
                arr[preIndex + gap] = arr[preIndex];
                preIndex -= gap;
            }
            arr[preIndex + gap] = current;
        }
    }
}

归并排序

1.动图演示

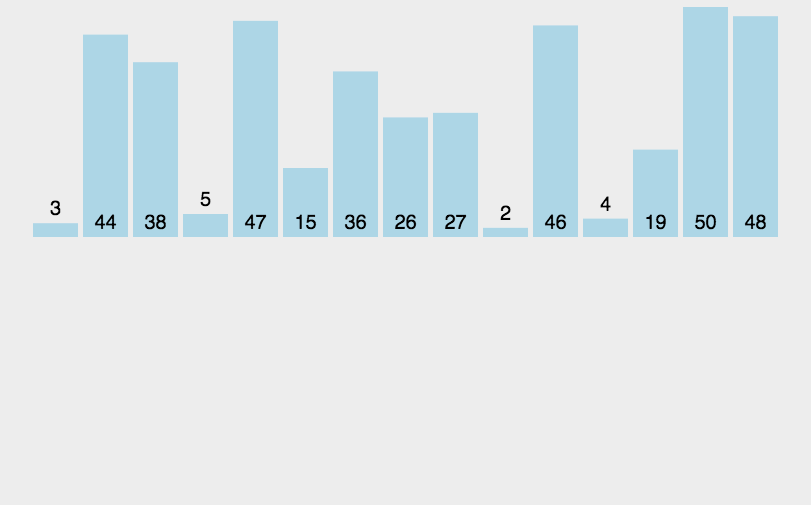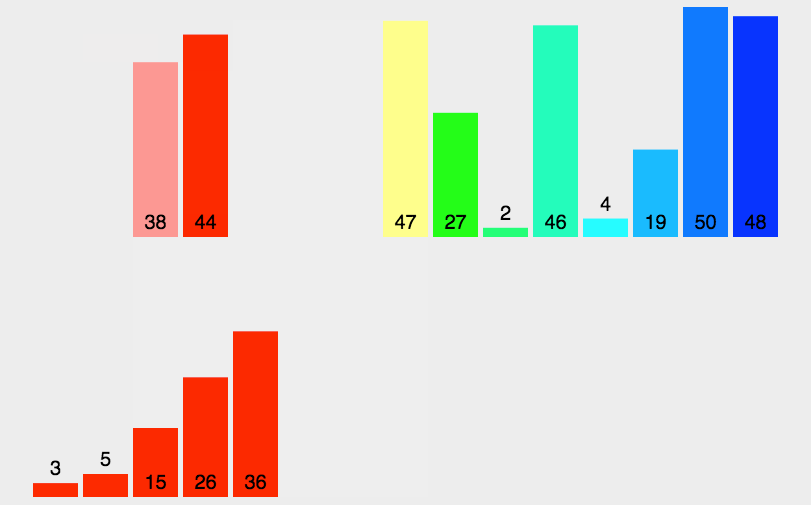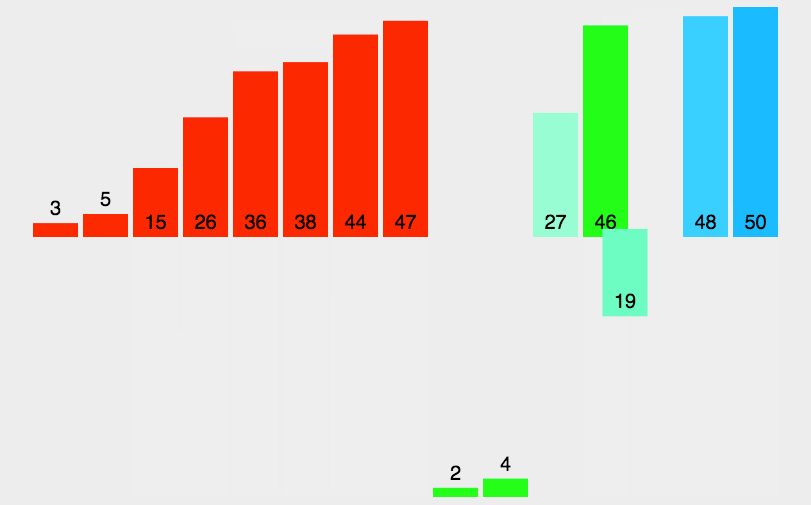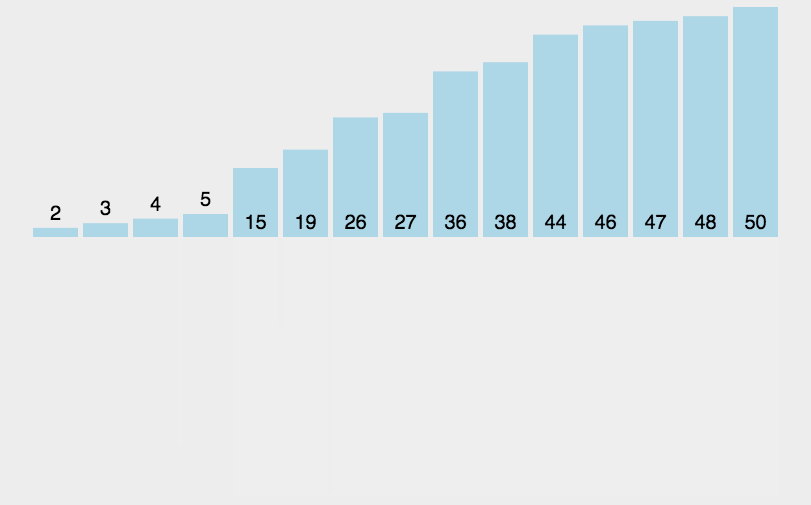
2.代码实现

private static void mergeSort(int[] arr, int leftIndex, int rightIndex) {
    if (leftIndex < rightIndex) {
        int middleIndex = (leftIndex + rightIndex) / 2; // 中间下标
        // 1.递归对左右两部分进行排序
        mergeSort(arr, leftIndex, middleIndex);
        mergeSort(arr, middleIndex + 1, rightIndex);
        // 2.合并左右两个有序数组
        merge(arr, leftIndex, middleIndex, rightIndex);
    }
}

private static void merge(int[] arr, int leftIndex, int middleIndex, int rightIndex) {
    int[] temp = new int[rightIndex - leftIndex + 1]; // 创建临时数组
    int i = leftIndex; // 左序列指针
    int j = middleIndex + 1; // 右序列指针
    int k = 0; // 临时数组指针
    while (i <= middleIndex && j <= rightIndex) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }
    // 把剩余左边元素填充到临时数组
    while (i <= middleIndex) {
        temp[k++] = arr[i++];
    }
    // 把剩余右边元素填充到临时数组
    while (j <= rightIndex) {
        temp[k++] = arr[j++];
    }
    // 把有序的临时数组数据回写到原数组
    for (int l = 0; l < temp.length; l++) {
        arr[l + leftIndex] = temp[l];
    }
}

快速排序

1.动图演示

2.代码实现

private static void quickSort(int[] arr, int leftIndex, int rightIndex) {
    if (leftIndex < rightIndex) {
        // 1.分区操作返回基准值的下标
        int partitionIndex = partition(arr, leftIndex, rightIndex);
        // 2.递归左右分区的数组
        quickSort(arr, leftIndex, partitionIndex - 1);
        quickSort(arr, partitionIndex + 1, rightIndex);
    }
}

private static int partition(int[] arr, int leftIndex, int rightIndex) {
    int pivotIndex = leftIndex; // 设定基准值
    int index = pivotIndex + 1; // 起始下标值
    // 将小于基准值得数据移到左边，大于基准值的放右边
    for (int i = index; i <= rightIndex; i++) {
        if (arr[i] < arr[pivotIndex]) {
            swap(arr, i, index);
            index ++;
        }
    }
    // 把基准值放到数组中间并返回基准值下标
    swap(arr, pivotIndex, index - 1);
    return index - 1;
}

// 交换数组中两个元素
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

堆排序

1.动图演示

2.代码实现

private static void heapSort(int[] arr) {
    // 1.构建大顶堆(从最后一个非叶子节点开始)
    for (int i = arr.length/2 - 1; i >= 0 ; i--) {
        adjustHeap(arr, i, arr.length); // 调整堆
    }
    // 2.将大顶堆得根元素放在数组的末尾
    for (int j = arr.length - 1; j > 0; j--) {
        swap(arr, 0, j);
        adjustHeap(arr, 0, j);
    }
}

private static void adjustHeap(int[] arr, int i, int length) {
    // 取出当前元素(可能一直移动)
    int temp = arr[i];
    for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
        // 当存在右节点且右节点大于左节点，标识向右移动
        if (k + 1 < length && arr[k] < arr[k + 1]) {
            k++;
        }
        // 如果节点大于根节点则交换
        if (arr[k] > temp) {
            swap(arr, i, k);
            i = k;
        } else {
            break;
        }
    }
}

// 交换数组中两个元素
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

计数排序

1.动图演示

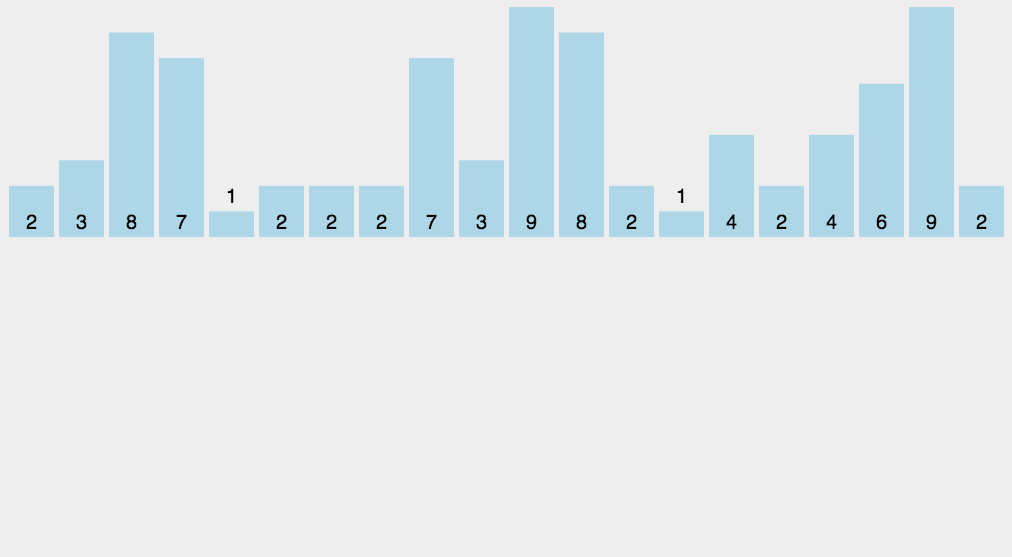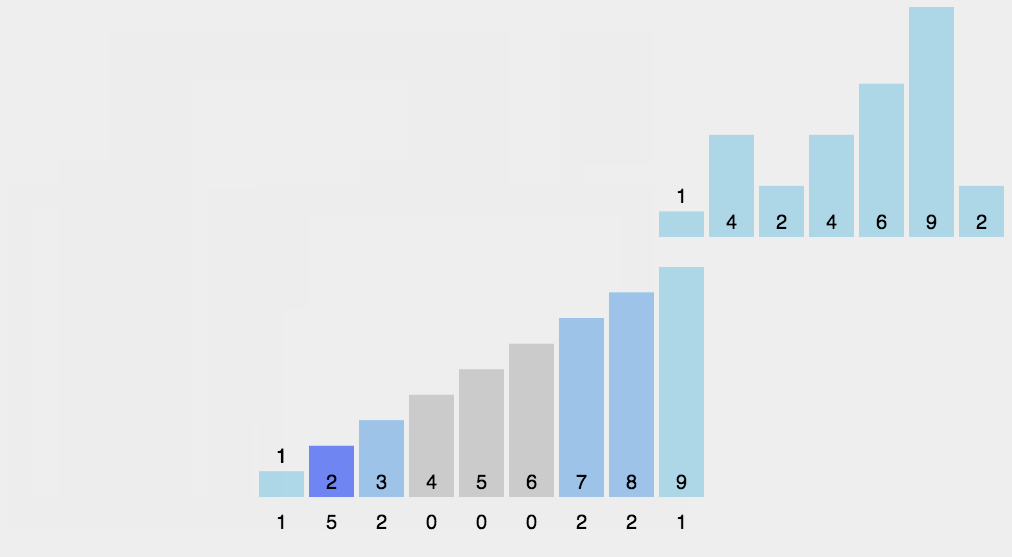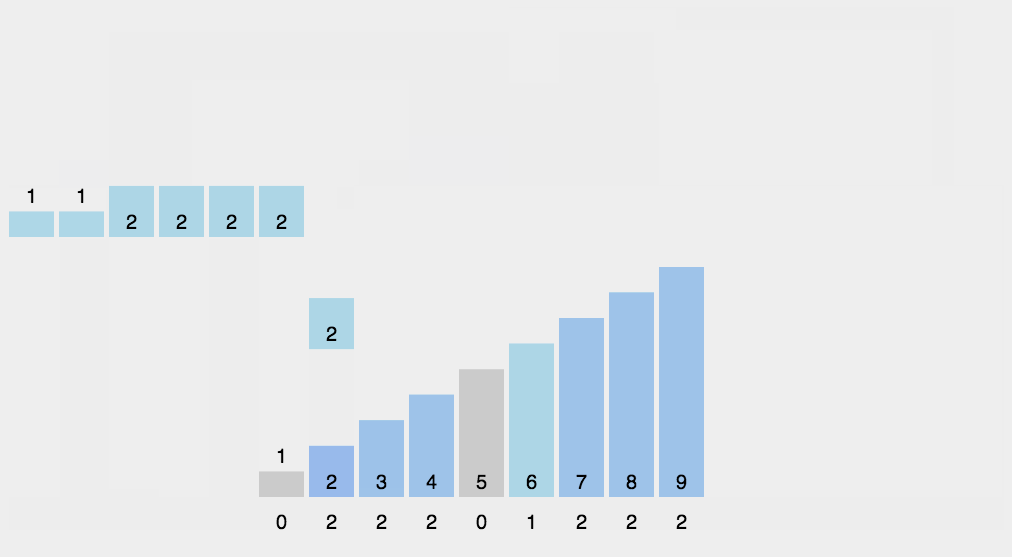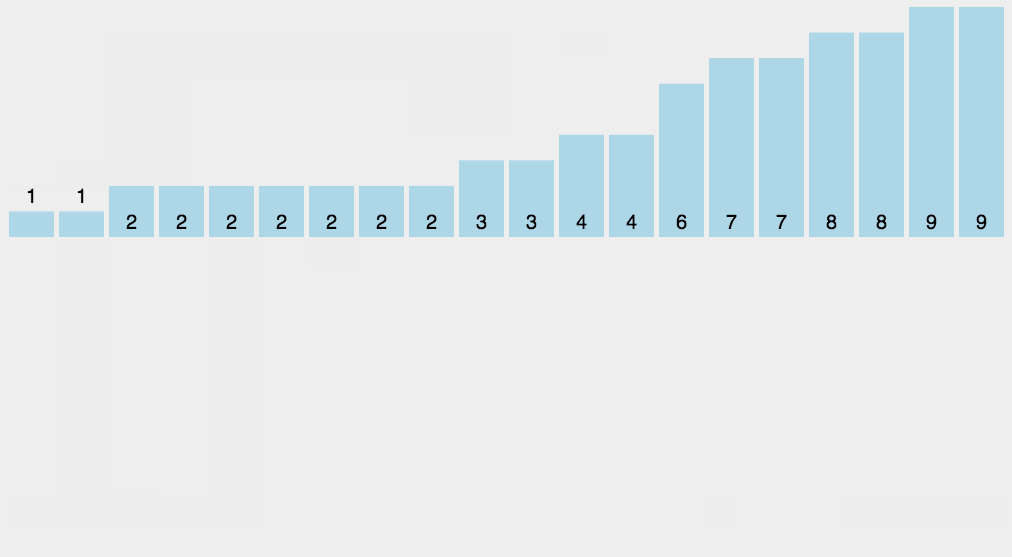
2.代码实现 

private static void countingSort(int[] arr, int maxValue) {
    int arrIndex = 0;
    // 构建计数桶
    int[] bucket = new int[maxValue + 1];
    for (int i = 0; i < arr.length; i++) {
        bucket[arr[i]] ++ ;
    }
    // 回写原数组
    for (int i = 0; i < bucket.length; i++) {
        while (bucket[i] > 0) {
            arr[arrIndex++] = i;
            bucket[i]--;
        }
    }
}

参考：十大经典排序算法