Python数据分析与挖掘实战(6章)
非原创,仅个人关于《Python数据分析与挖掘实战》的学习笔记
窃漏电数据分析
导入相关库
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import xlrd
# 解决中文乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 忽略警告
warnings.filterwarnings("ignore")
数据读取
# 定义文件路径
inputfile_path = '/Notebook/读书笔记/Python数据分析与挖掘实战/data/missing_data.xls'
# outputfile_path = '/Notebook/读书笔记/Python数据分析与挖掘实战/data/missing_data_processed.xls'
# 读取Excel文件
data = pd.read_excel(inputfile_path,header=None)
type(data)
pandas.core.frame.DataFrame
data
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 235.8333 | 324.0343 | 478.3231 |
| 1 | 236.2708 | 325.6379 | 515.4564 |
| 2 | 238.0521 | 328.0897 | 517.0909 |
| 3 | 235.9063 | NaN | 514.8900 |
| 4 | 236.7604 | 268.8324 | NaN |
| 5 | NaN | 404.0480 | 486.0912 |
| 6 | 237.4167 | 391.2652 | 516.2330 |
| 7 | 238.6563 | 380.8241 | NaN |
| 8 | 237.6042 | 388.0230 | 435.3508 |
| 9 | 238.0313 | 206.4349 | 487.6750 |
| 10 | 235.0729 | NaN | NaN |
| 11 | 235.5313 | 400.0787 | 660.2347 |
| 12 | NaN | 411.2069 | 621.2346 |
| 13 | 234.4688 | 395.2343 | 611.3408 |
| 14 | 235.5000 | 344.8221 | 643.0863 |
| 15 | 235.6354 | 385.6432 | 642.3482 |
| 16 | 234.5521 | 401.6234 | NaN |
| 17 | 236.0000 | 409.6489 | 602.9347 |
| 18 | 235.2396 | 416.8795 | 589.3457 |
| 19 | 235.4896 | NaN | 556.3452 |
| 20 | 236.9688 | NaN | 538.3470 |
data.columns
Index([0, 1, 2], dtype='int64')
len(data)
21
数据预处理
拉格朗日插值
import pandas as pd
from scipy.interpolate import lagrange
# 定义拉格朗日插值函数
def ployinterp_column(s, n, k=5):
# 确保索引范围在合法范围内
start = max(0, n - k)
end = min(len(s), n + k + 1)
# 取前后 k 个数据点,排除掉索引为 n 的点
y = s[list(range(start, n)) + list(range(n + 1, end))]
y = y.dropna() # 剔除空值
if len(y) < 2:
# 如果剩下的点不足以进行插值,返回原始值或其他处理方式
return s[n]
return lagrange(y.index, y.values)(n) # 插值并返回插值结果
# 逐个元素判断是否需要插值
for i in data.columns:
for j in range(len(data)):
if pd.isna(data.at[j, i]): # 如果为空即插值
try:
data.at[j, i] = ployinterp_column(data[i], j)
except ValueError as e:
print(f"插值错误在列 {i} 的索引 {j}: {e}")
data
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 235.833300 | 324.034300 | 478.323100 |
| 1 | 236.270800 | 325.637900 | 515.456400 |
| 2 | 238.052100 | 328.089700 | 517.090900 |
| 3 | 235.906300 | 203.462116 | 514.890000 |
| 4 | 236.760400 | 268.832400 | 493.352591 |
| 5 | 237.151181 | 404.048000 | 486.091200 |
| 6 | 237.416700 | 391.265200 | 516.233000 |
| 7 | 238.656300 | 380.824100 | 493.342382 |
| 8 | 237.604200 | 388.023000 | 435.350800 |
| 9 | 238.031300 | 206.434900 | 487.675000 |
| 10 | 235.072900 | 237.348072 | 609.193564 |
| 11 | 235.531300 | 400.078700 | 660.234700 |
| 12 | 235.314951 | 411.206900 | 621.234600 |
| 13 | 234.468800 | 395.234300 | 611.340800 |
| 14 | 235.500000 | 344.822100 | 643.086300 |
| 15 | 235.635400 | 385.643200 | 642.348200 |
| 16 | 234.552100 | 401.623400 | 618.197198 |
| 17 | 236.000000 | 409.648900 | 602.934700 |
| 18 | 235.239600 | 416.879500 | 589.345700 |
| 19 | 235.489600 | 420.748600 | 556.345200 |
| 20 | 236.968800 | 408.963200 | 538.347000 |
数据转换
那什么样的数据才是存在窃漏电的情况呢?
书中,提出了一套指标公式。通过公式,将上面各种复杂繁多的数据变换为三项指标的简单数据。很可惜,书中并没有将数据转换的过程写出来。直接是给了结果,如下所示:
# model.xls

模型构建
构建窃漏电用户识别模型
# 判断用户是否窃漏电,这是一种分类预测。
model_path = '/Notebook/读书笔记/Python数据分析与挖掘实战/data/model.xls'
# 随机函数,用来打乱数据
from random import shuffle
# 读取数据
model_data = pd.read_excel(model_path)
type(model_data)
pandas.core.frame.DataFrame
model_data
| 电量趋势下降指标 | 线损指标 | 告警类指标 | 是否窃漏电 | |
|---|---|---|---|---|
| 0 | 4 | 1 | 1 | 1 |
| 1 | 4 | 0 | 4 | 1 |
| 2 | 2 | 1 | 1 | 1 |
| 3 | 9 | 0 | 0 | 0 |
| 4 | 3 | 1 | 0 | 0 |
| ... | ... | ... | ... | ... |
| 286 | 4 | 1 | 2 | 0 |
| 287 | 1 | 0 | 2 | 0 |
| 288 | 5 | 1 | 2 | 1 |
| 289 | 2 | 1 | 0 | 0 |
| 290 | 4 | 1 | 0 | 0 |
291 rows × 4 columns
model_data = model_data.sample(frac=1).reset_index(drop=True)
model_data
| 电量趋势下降指标 | 线损指标 | 告警类指标 | 是否窃漏电 | |
|---|---|---|---|---|
| 0 | 3 | 1 | 2 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 2 | 3 | 0 | 2 | 0 |
| 3 | 3 | 1 | 1 | 0 |
| 4 | 4 | 1 | 1 | 1 |
| ... | ... | ... | ... | ... |
| 286 | 5 | 0 | 1 | 0 |
| 287 | 5 | 1 | 1 | 1 |
| 288 | 4 | 0 | 2 | 0 |
| 289 | 4 | 0 | 0 | 0 |
| 290 | 6 | 0 | 0 | 0 |
291 rows × 4 columns
# 假设 model_data 是你的数据框
p = 0.8 # 设置训练数据比例
split_index = int(len(model_data) * p)
# 使用 iloc 按位置索引来分割数据集
train = model_data.iloc[:split_index, :]
test = model_data.iloc[split_index:, :]
LM神经网络(KMeras)
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# 读取数据
model_path = '/Notebook/读书笔记/Python数据分析与挖掘实战/data/model.xls'
model_data = pd.read_excel(model_path)
# 打乱数据
# model_data = model_data.sample(frac=1).reset_index(drop=True)
# 设置训练数据比例
p = 0.8
split_index = int(len(model_data) * p)
# 分割数据集
train = model_data.iloc[:split_index, :]
test = model_data.iloc[split_index:, :]
# 假设最后一列是标签
X_train = train.iloc[:, :-1].values
y_train = train.iloc[:, -1].values
X_test = test.iloc[:, :-1].values
y_test = test.iloc[:, -1].values
# 数据归一化
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# 定义 LM 神经网络模型
mlp = MLPClassifier(hidden_layer_sizes=(100,), activation='relu', solver='adam', max_iter=2000, random_state=42)
# 训练模型
mlp.fit(X_train, y_train)
# 预测
y_pred = mlp.predict(X_test)
# 评估模型
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)
print("准确率:", accuracy)
print("混淆矩阵:\n", conf_matrix)
print("分类报告:\n", class_report)
准确率: 0.9491525423728814
混淆矩阵:
[[54 3]
[ 0 2]]
分类报告:
precision recall f1-score support
0 1.00 0.95 0.97 57
1 0.40 1.00 0.57 2
accuracy 0.95 59
macro avg 0.70 0.97 0.77 59
weighted avg 0.98 0.95 0.96 59
import matplotlib.pyplot as plt
import seaborn as sns
# 绘制混淆矩阵
plt.figure(figsize=(6, 4))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Blues')
plt.title('混淆矩阵')
plt.xlabel('预测')
plt.ylabel('实际')
plt.show()

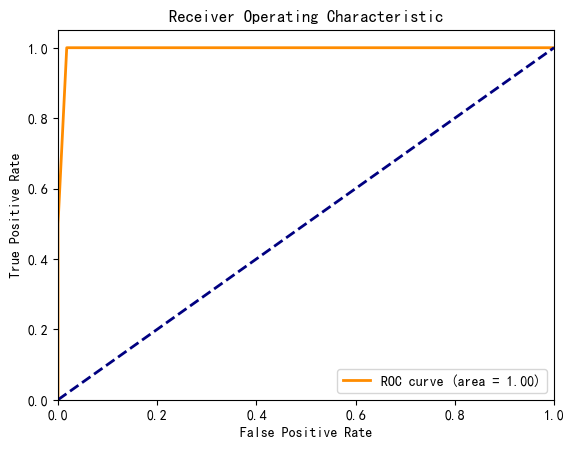
ROC曲线评价
from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt
# 预测测试集的概率
y_prob = mlp.predict_proba(X_test)[:, 1] # 假设类别1是正类
# 计算ROC曲线的FPR和TPR
fpr, tpr, thresholds = roc_curve(y_test, y_prob, pos_label=1) # pos_label根据你的数据集可能需要调整
# 计算AUC值
roc_auc = auc(fpr, tpr)
# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
CART决策树模型
决策树是一种流行的机器学习算法,用于分类和回归任务。它通过递归地将数据集分割成越来越小的子集,直到满足停止条件,从而构建决策树。每个内部节点代表一个特征上的测试,每个分支代表测试的结果,每个叶节点代表一个预测值。
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
import matplotlib.pyplot as plt
# 读取数据
model_path_cart = '/Notebook/读书笔记/Python数据分析与挖掘实战/data/model.xls'
model_data_cart = pd.read_excel(model_path_cart)
# 打乱数据
# model_data = model_data.sample(frac=1).reset_index(drop=True)
# 设置训练数据比例
p = 0.8
split_index_cart = int(len(model_data_cart) * p)
# 分割数据集
train_cart = model_data.iloc[:split_index, :]
test_cart = model_data.iloc[split_index:, :]
# 假设最后一列是标签
X_train_cart = train_cart.iloc[:, :-1].values
y_train_cart = train_cart.iloc[:, -1].values
X_test_cart = test_cart.iloc[:, :-1].values
y_test_cart = test_cart.iloc[:, -1].values
# 数据归一化
scaler_cart = MinMaxScaler()
X_train_cart = scaler.fit_transform(X_train_cart)
X_test_cart = scaler.transform(X_test_cart)
# 创建决策树
dt = DecisionTreeClassifier(random_state=42)
# 训练模型
dt.fit(X_train_cart, y_train_cart)
# 预测
y_pred_cart = dt.predict(X_test_cart)
#评估模型
accuracy_cart = accuracy_score(y_test_cart, y_pred_cart)
conf_matrix_cart = confusion_matrix(y_test_cart, y_pred_cart)
class_report_cart = classification_report(y_test_cart, y_pred_cart)
print("准确率:", accuracy_cart)
print("混淆矩阵:\n", conf_matrix_cart)
print("分类报告:\n", class_report_cart)
准确率: 0.9491525423728814
混淆矩阵:
[[54 3]
[ 0 2]]
分类报告:
precision recall f1-score support
0 1.00 0.95 0.97 57
1 0.40 1.00 0.57 2
accuracy 0.95 59
macro avg 0.70 0.97 0.77 59
weighted avg 0.98 0.95 0.96 59
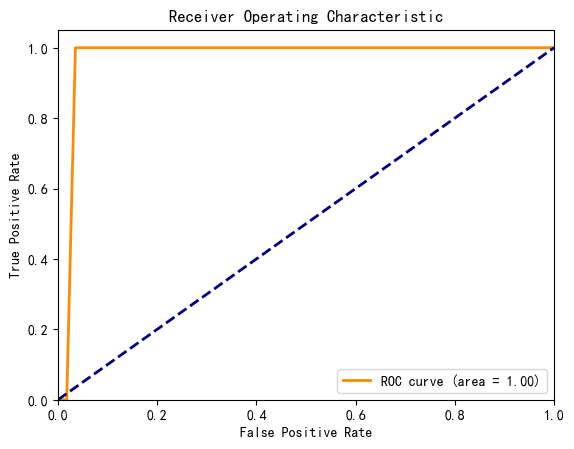
绘制ROC曲线
#绘制ROC曲线
from sklearn.metrics import roc_curve, auc
# 假设二分类问题,正类为1
y_prob_cart = dt.predict_proba(X_test_cart)[:, 1]
fpr_cart, tpr_cart, thresholds_cart = roc_curve(y_test_cart, y_prob_cart, pos_label=1)
roc_auc_cart = auc(fpr, tpr)
plt.figure()
plt.plot(fpr_cart, tpr_cart, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc_cart)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
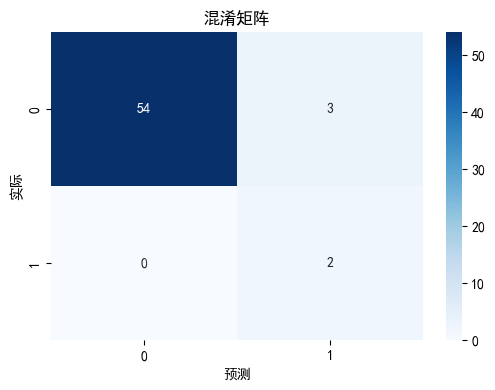
import matplotlib.pyplot as plt
import seaborn as sns
# 绘制混淆矩阵
plt.figure(figsize=(6, 4))
sns.heatmap(conf_matrix_cart, annot=True, fmt='d', cmap='Blues')
plt.title('混淆矩阵')
plt.xlabel('预测')
plt.ylabel('实际')
plt.show()
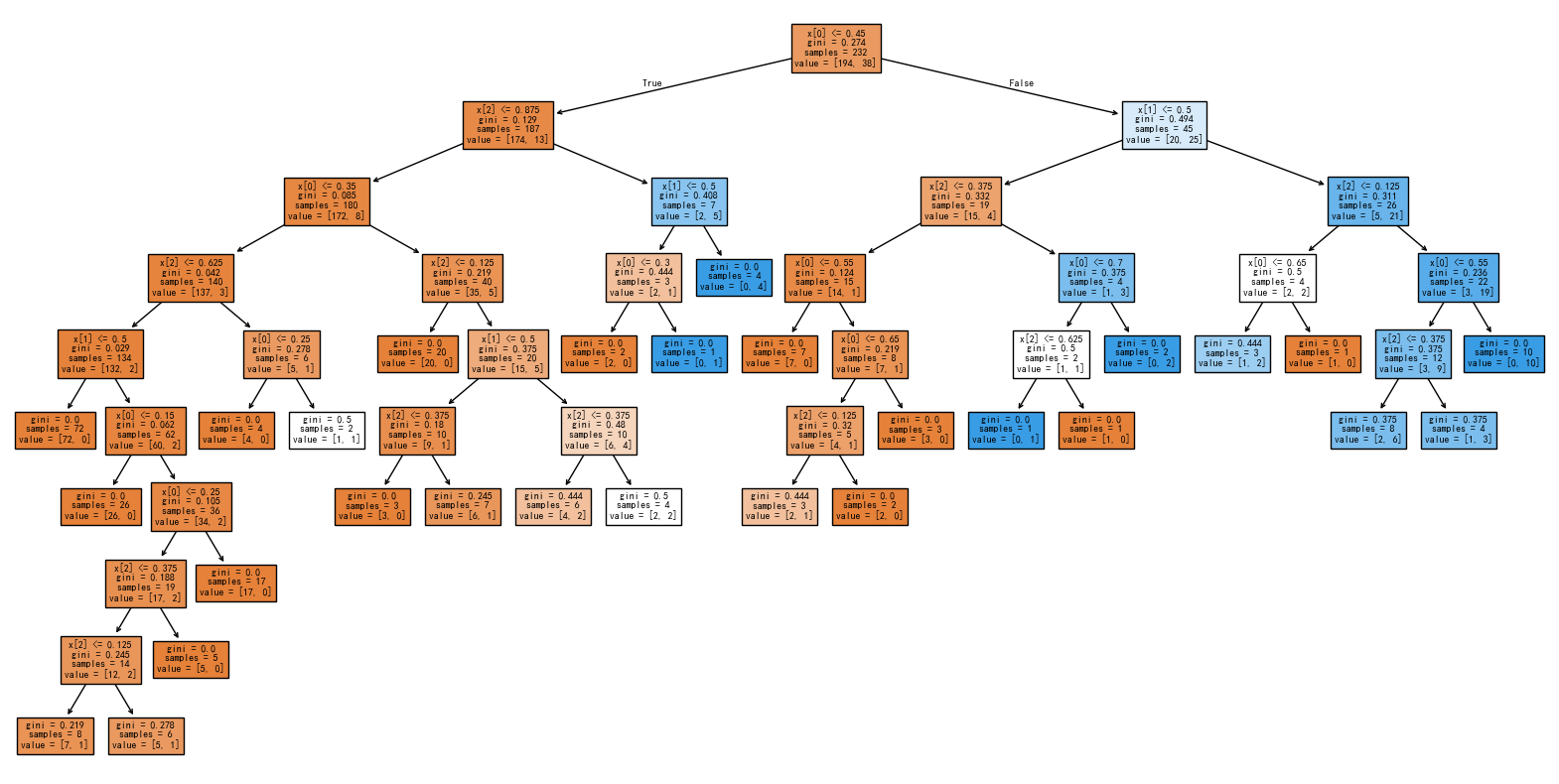
# 可视化决策树
plt.figure(figsize=(20,10))
plot_tree(dt, filled=True)
plt.show()
本文来自博客园,作者:ZhouSpeaks,转载请注明原文链接:https://www.cnblogs.com/zhouwp/p/18220701


 浙公网安备 33010602011771号
浙公网安备 33010602011771号