Loading

统计学

统计学

本文是基于https://mp.weixin.qq.com/s/iWu_qmoseRCezOwMKu9UNw的学习笔记，版权归原作者所有。

import seaborn as sns
import warnings
warnings.filterwarnings("ignore")

描述性统计学

集中趋势

  • 平均数
# 算术平均

import numpy as np
data_Arithmetic = np.arange(10)

data_Arithmetic

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np.mean(data_Arithmetic)

4.5

# 几何平均

几何平均数是一组正数乘积的 n 次方根，其中 n 是这组数值的个数。

\[Geometric Mean=\sqrt[n]{x_1*x_2...x_n} \]

# 使用 numpy.random.rand() 生成均匀分布的随机数，范围在 [0, 1) 之间
# 使用 numpy.random.randn() 生成服从标准正态分布的随机数。
# 使用 numpy.random.randint() 生成一个整数随机数。

from scipy import stats as sts
np.random.seed(42)
data_Geometric = np.random.rand(10)*10

data_Geometric

array([3.74540119, 9.50714306, 7.31993942, 5.98658484, 1.5601864 ,
       1.5599452 , 0.58083612, 8.66176146, 6.01115012, 7.08072578])

sts.gmean(data_Geometric)

3.8996138296750384

# 调和平均数

如果有 n 个正数 x₁, x₂, ..., xn，则调和平均数（harmonic mean）为 n 除以这组数值的倒数的平均值，表达式如下：

\[Harmonic Mean=\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}} \]

np.random.seed(42)
data_Harmonic = np.random.rand(10)*10

data_Harmonic

array([3.74540119, 9.50714306, 7.31993942, 5.98658484, 1.5601864 ,
       1.5599452 , 0.58083612, 8.66176146, 6.01115012, 7.08072578])

sts.hmean(data_Harmonic)

2.4375258352568157
  • 中位数
np.median(data_Harmonic)

5.998867479701227
  • 众数
from scipy import stats as sts
# 创建一个包含重复元素的NumPy数组
data_modes = np.array([1, 2, 2, 3, 4, 4, 4, 5, 5, 5, 5])
sts.mode(data_modes)

ModeResult(mode=array([5]), count=array([4]))

离散趋势

  • 分位数
# 四分位数用3个分位数，将数据等分成4个部分。

data_modes

array([1, 2, 2, 3, 4, 4, 4, 5, 5, 5, 5])

sts.scoreatpercentile(data,25)

sts.scoreatpercentile(data,50)

sts.scoreatpercentile(data,75)

import seaborn as sns

sns.boxplot(data=data)

data_modes

array([1, 2, 2, 3, 4, 4, 4, 5, 5, 5, 5])

# 极差：极差又称范围误差或全距，是指一组数据中最大值与最小值的差
np.ptp(data_modes)

4

# 四分位距：四分位距是上四分位数与下四分位数之差
sts.scoreatpercentile(data_modes,75)-sts.scoreatpercentile(data_modes,25)

2.5
  • 方差

方差（Variance）是用来衡量一组数据的离散程度或分散程度的统计量。对于一组数据集，【总体方差】的计算公式如下：

\[\sigma^2=\frac{\sum_{i=1}^{n}(X_i-\overline X)^2}{n} \]

  • n是数据集中的观测值的个数
  • \(X_i是第i个观测值\)
  • \(\overline X 是所有观测值的平均值\)

结论：\(\sigma 越大，数据集相对平均值更分散；\sigma越小，数据集相对平均值更集中\)

【样本方差】的计算公式如下：

\[S^2=\frac{\sum_{i=1}^{n}(X_i-\overline X)^2}{n-1} \]

# ddof=1时,分母为n-1;ddof=0时,分母为n

# 样本方差
sts.tvar(data_modes,ddof=1)

2.054545454545454

# 总体方差
sts.tvar(data_modes,ddof=0)

1.8677685950413219
  • 标准差

\[\sigma=\sqrt{\frac{\sum_{i=1}^{n}(X_i-\overline X)^2}{n-1}} \]

# 样本标准差
sts.tstd(data_modes,ddof=1)

1.4333685689819815

# 总体标准差
sts.tstd(data_modes,ddof=0)

1.3666633071248098
  • 变异系数

对不同变量或不同数组的离散程度进行比较时，如果它们的平均水平和计量单位都相同，才能利用上述指标进行分析，否则需利用变异系数来比较它们的离散程度。变异系数又称为离散系数，是一组数据中的极差、四分位差或标准差等离散指标与算术平均数的比率。

sts.tstd(data_modes)/sts.tmean(data_modes)

0.39417635647004495

分布形状

  • 偏度

  • 偏度系数是对分布偏斜程度的测度，通常用SK表示。偏度衡量随机变量概率分布的不对称性，是相对于平均值不对称程度的度量

  • 当偏度系数为正值时，表示正偏离差数值较大，可以判断为正偏态或右偏态

  • 当偏度系数为负值时，表示负偏离差数值较大，可以判断为负偏态或左偏态。偏度系数的绝对值越大，表示偏斜的程度就越大。

from scipy import stats as sts
data_modes

array([1, 2, 2, 3, 4, 4, 4, 5, 5, 5, 5])

# bias=False 代表计算的是总体偏度，bias=True 代表计算的是样本偏度
sts.skew(data_modes,bias=False)

-0.7079471982963713
  • 峰度

峰度描述的是分布集中趋势高峰的形态，通常与标准正态分布相比较。在归化到同一方差时，若分布的形状比标准正态分布更“瘦”、更“高”，则称为尖峰分布；若比标准正态分布更“矮”、更“胖”，则称为平峰分布。

峰度系数是对分布峰度的测度，通常用K表示：

由于标准正态分布的峰度系数为0，所以当峰度系数大于0时为尖峰分布，当峰度系数小于0时为平峰分布。

sts.kurtosis(data_modes,bias=False)

-0.8356175111598398

推断统计学

\(\Rightarrow\)正态分布

\(\Rightarrow\)标准正态分布

\(\Rightarrow\)t分布，样本均值推断

\(\Rightarrow\)F分布，方差的比较

\(\Rightarrow\)卡方分布，数据的拟合优度检验

\(\blacksquare\) 正态分布

ztfb_data = np.random.normal(3,4,1000)

sns.histplot(ztfb_data,kde=True)

<Axes: ylabel='Count'>

\(\blacksquare\) 标准正态分布

bzztfb_data = np.random.standard_normal(1000)
sns.histplot(bzztfb_data,kde=True)

<Axes: ylabel='Count'>

\(->t分布\)

t分布是一种概率分布，用于小样本情况下对总体均值的推断。当样本容量较小或总体方差未知时，使用T分布进行推断更准确。T分布的形状类似于正态分布，但尾部较宽。T分布的自由度（degreesof freedom）决定了其形状。

t_data = np.random.standard_t(10,1000) #10 表示自由度,1000,随机数个数
sns.histplot(t_data,kde=True)

<Axes: ylabel='Count'>

\(->F分布\)

F分布是一种概率分布，用于比较两个样本方差的差异。F分布常用于方差分析和回归分析中。F分布的形状取决于两个自由度参数，分子自由度和分母自由度。

dfn = 5  # 分子自由度
dfd = 10  # 分母自由度
size = 1000  # 生成1000个随机数

data = np.random.f(dfn, dfd, size=size)
sns.histplot(data, kde=True)

<Axes: ylabel='Count'>

\(->卡方分布\)

卡方分布是一种概率分布，用于检验观察值与理论值之间的拟合优度。卡方分布常用于拟合优度检验、独立性检验和方差分析中。卡方分布的自由度参数决定了其形状。

df = 5  # 自由度
size = 1000  # 生成1000个随机数

data = np.random.chisquare(df, size)
sns.histplot(data, kde=True)

<Axes: ylabel='Count'>

区间估计

区间估计经常用于质量控制领域来检测生产过程是否正常运行或者在“控制之中” ，也可以用来监控互联网领域各类数据指标是否在正常区间。

假设样本容量:

\[n= \frac{(Z_{\alpha/2})^2\sigma^2}{E^2} \]

均值

$ 如果 n>=30:
$

\(\Rightarrow总体\sigma 已知：\overline X \pm Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\)

\(\Rightarrow总体\sigma 未知：\overline X \pm Z_{\alpha/2}\frac{S}{\sqrt{n}}\)

$ 如果 n<30:
$

\(\Rightarrow总体\sigma 已知：\overline X \pm Z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\)

\(\Rightarrow总体\sigma 未知：\overline X \pm Z_{\alpha/2}\frac{S}{\sqrt{n}}\)

首先读取数据，我们就继续用前面的data

# data

计算均值\(\overline X\)

mean = data.mean()

mean

5.086808771119212

计算样本标准差\(\sigma\)

std = sts.tstd(data,ddof=1)

std

2.996204500297233

import numpy as np
import scipy.stats
from scipy import stats as sts

def mean_interval(mean=None, sigma=None,std=None,n=None,confidence_coef=0.95):
    """
    mean:样本均值
    sigma: 总体标准差
    std: 样本标准差
    n:   样本量
    # confidence_coef：置信系数
    # confidence_level:置信水平 置信度
    alpha:显著性水平
    功能：构建总体均值的置信区间
    """
    alpha = 1 - confidence_coef
    z_score = scipy.stats.norm.isf(alpha / 2)            # z分布临界值
    t_score = scipy.stats.t.isf(alpha / 2, df = (n-1) )  # t分布临界值
   
    if n >= 30: 
        if sigma != None:
            me = z_score * sigma / np.sqrt(n)
            print("大样本，总体 sigma 已知：z_score:",z_score)
        elif sigma == None:
            me = z_score * std / np.sqrt(n)
            print("大样本，总体 sigma 未知 z_score",z_score)
        lower_limit = mean - me
        upper_limit = mean + me
    if n < 30 :
        if sigma != None:
            me = z_score * sigma / np.sqrt(n)
            print("小样本，总体 sigma 已知 z_score * sigma / np.sqrt(n) \n z_score = ",z_score)
        elif sigma == None:
            me = t_score * std / np.sqrt(n)
            print("小样本，总体 sigma 未知 t_score * std / np.sqrt(n) \n t_score = ",t_score)
            
        print("t_score:",t_score)
        lower_limit = mean - me
        upper_limit = mean + me
    
    return (round(lower_limit, 1), round(upper_limit, 1))

比例

区间估计

\[\overline p \pm Z_{\frac{\alpha}{2}}\sqrt{\frac{\overline p(1-\overline p)}{n}} \]

其中样本容量，$$ n= \frac{(Z_{\alpha/2})2\sigma2}{E^2}$$

def proportion_interval(p=None, n=None, confidence_coef =0.95):
    """
    p: 样本比例
    n: 样本量
    confidence_coef: 置信系数
    功能：构建总体比例的置信区间
    """
    alpha = 1 - confidence_coef
    z_score = scipy.stats.norm.isf(alpha / 2)  # z分布临界值
    
    me = z_score * np.sqrt((p * (1 - p)) / n) 
    lower_limit = p - me
    upper_limit = p + me
    
    return (round(lower_limit, 3), round(upper_limit, 3))

假设检验

单个总体的假设检验

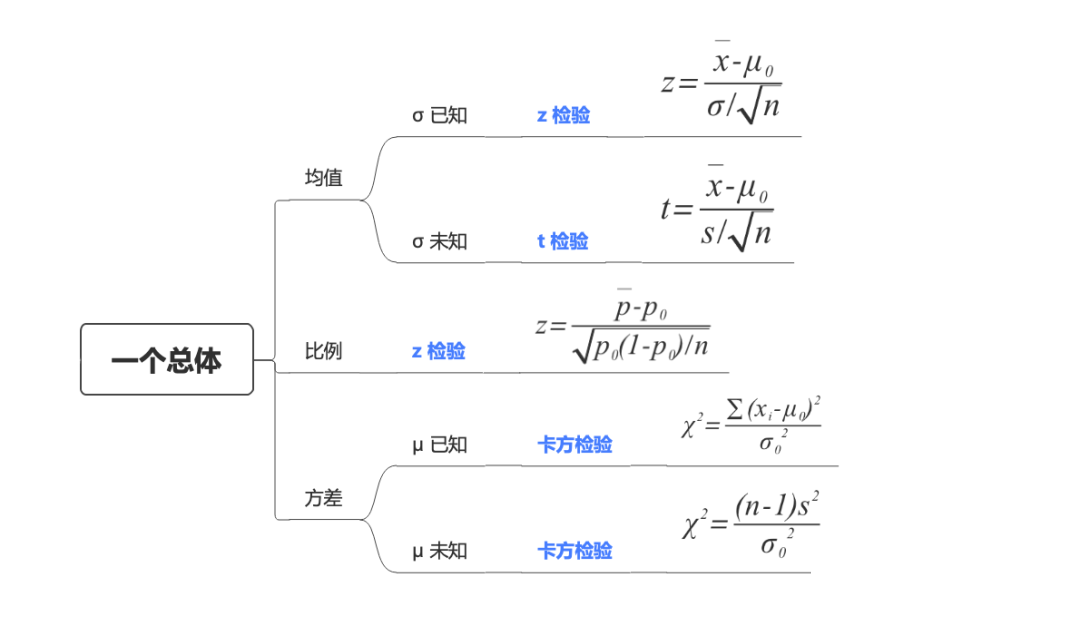
均值

  • \(\sigma已知-z检验\)

\[z=\frac{{\overline {x}}-\mu_0}{\frac{\sigma}{\sqrt{n}}} \]

例：监督部门称了50包标重500g的红糖，均值是498.35g，少于所标的500g。对于厂家生产的这批红糖平均起来是否够份量，需要统计检验。

\(H_0:\mu=500\)，\(H_1:\mu<500\)

其中\(\mu\)是指均值

from scipy import stats
import scipy.stats
import numpy as np
import pandas  as pd
import statsmodels.stats.weightstats

data = [493.01,498.83,494.16,500.39,497.63,499.72,493.41,498.97,501.94,503.45,497.47,494.19,500.99,495.81,499.63,494.91,498.90,502.43,491.34,497.50,505.95,496.56,501.66,492.02,497.68,493.48,505.40,499.21,505.84,499.41,505.65,500.51,489.53,496.55,492.26,498.91,496.65,496.38,497.16,498.91,490.98,499.97,501.21,502.85,494.35,502.96,506.21,497.66,504.66,492.11]

z,pval = statsmodels.stats.weightstats.ztest(data,value=500,alternative='smaller')

# statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative='two-sided', usevar='pooled', ddof=1)

# x1：要测试的第一组（样本）的数据。
# x2：这是一个可选参数，表示如果进行双样本 z 检验，则为第二组（样本）的数据。如果不提供，则假定为单样本 z 检验。
# value：这是零假设的值（零假设下的总体均值）。默认设置为 0。
# alternative：此参数指定备择假设，可以取值为 'two-sided'、'larger' 或 'smaller'。默认为 'two-sided'。
# usevar：此参数指定是否假设等方差（'pooled'）或不等方差（'unequal'）。默认为 'pooled'。
# ddof：标准差的自由度调整。默认为 1。

alternative 参数指定备择假设的类型:

two-sided(双侧检验)：

  • 零假设（H0）：总体参数等于指定的值（value）。
  • 备择假设（H1）：总体参数不等于指定的值（value）。
  • 这是默认值。在双侧检验中，您关心的是总体参数是否与指定值相等，但不关心它是偏大还是偏小。

larger'(大于检验)：

  • 零假设（H0）：总体参数等于或小于指定的值（value）

备择假设（H1）：总体参数大于指定的值（value

在这种情况下，您关心的是总体参数是否大。

'smaller'（小于检验）：

  • 零假设（H0）：总体参数等于或大于指定的值（value）。
  • 备择假设（H1）：总体参数小于指定的值（value）。
  • 在这种情况下，您关心的是总体参数是否偏小。
z

-2.6961912076362085

pval

0.0035068696715304876

P=0.0035<0.05

选择显著性水平 0.05 的话，P=0.0035 < 0.05, 故应该拒绝原假设。具体来说就是该结果倾向于支持平均重量小于500g的备则假设。

如果你进行了一个 Z 检验，P 值通常是通过标准正态分布表（z-table）或计算正态分布的累积分布函数 (CDF) 得到的。Z 检验的 P 值表示观察到的 Z 统计量以上或以下的面积（概率）。

  • \(\sigma未知-t检验\)

\[t=\frac{{\overline {x}}-\mu_0}{\frac{S}{\sqrt{n}}} \]

汽车厂商声称其发动机排放标准的一个指标平均低于20个单位。
在抽查了10台发动机之后,得到下面的排放数据:17.0 21.7 17.9 22.9 20.7 22.4 17.3 21.8 24.2 25.4
该样本均值为21.13.究竟能否由此认为该指标均值超过20?

\(H_0:\mu=20\)，\(H_1:\mu>20\)

data = [17.0, 21.7, 17.9, 22.9, 20.7, 22.4, 17.3, 21.8, 24.2, 25.4]

t, pval = scipy.stats.ttest_1samp(a = data, popmean=20,alternative = 'greater')

t

1.2335757753252792

pval

0.12430247775898183

选择显著性水平 0.05 的话，P=0.1243 > 0.05, 故无法拒绝原假设。具体来说就是该结果无法支持指标均值超过20的备则假设。

比例

  • z检验

\[z=\frac{{\overline {p}}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} \]

例：一个总体比例的假设检验(指定比例和样本比例)

# 略

方差

  • \(\mu\)已知-卡方检验

\[\chi^2=\frac{\sum(x_i-\mu_0)^2}{\sigma_0^2} \]

  • \(\mu\)未知-卡方检验

\[\chi^2=\frac{(n-1)S^2}{\sigma_0^2} \]

例：一个总体方差的假设检验（指定方差和样本方差）

某市中心车站为规范化提升市民对于公交车到站时间的满意度，对于公交车的到站时间管理做了规定，标准是到站时间的方差不超过4。为了检验时间的到站时间的方差是否过大，随机抽取了24辆公交车的到站时间组成一个样本，得到的样本方差是\(s^2=4.9\)，假设到站时间的总体分布符合正态分布，请分析总体方差是否过大。

分析过程：由于研究的是方差是否过大，因此选择上侧检验比较合适,备择假设是方差大于4，于是我们有了原假设和备择假设

\(H_0:\sigma^2<=4\)，\(H_1:\sigma^2>4\)

scipy.stats.chi2 是 SciPy 库中用于处理卡方分布（Chi-square distribution）的模块。卡方分布通常与统计学中的假设检验相关，特别是在分析分类数据的时候。

import numpy as np
from scipy import stats

def chi2test(sample_var, sample_num,sigma_square,side, alpha=0.05):
    '''
    参数：
    sample_var--样本方差
    sample_num--样本容量
    sigma_square--H0方差
    返回值：
    pval
    '''
    # 这个公式计算的是卡方统计量（Chi-Square Statistic）用于进行方差检验（Variance Test）的值。
    chi_square =((sample_num-1)*sample_var)/(sigma_square)
    p_value = None
    if side == 'two-sided':
        #累积分布函数
        p = stats.chi2(df=sample_num-1).cdf(chi_square)
        p_value = 2*np.min([p, 1-p])
    elif side == 'less':
        #累积分布函数
        p_value = stats.chi2(df=sample_num-1).cdf(chi_square)
    elif side == 'greater':
        #stats.chi2.sf 是 SciPy 中卡方分布的生存函数（Survival Function）的一个方法。生存函数指的是一个随机变量大于某个值的概率。
        p_value = stats.chi2(df=sample_num-1).sf(chi_square)
    return chi_square,p_value

chi_square =((sample_num-1)*sample_var)/(sigma_square)，这个公式计算的是卡方统计量（Chi-Square Statistic）用于进行方差检验（Variance Test）的值。

假设你有一个样本，你想要检验这个样本的方差是否与某个已知的方差\(\sigma^2\)不同。卡方统计量的计算涉及到样本方差、样本容量和给定的方差。

\[X^2=\frac{(n-1)S^2}{\sigma^2} \]

$

  • X^2是卡方统计量;
  • n是样本容量;
  • s^2是样本方差;
  • \sigma^2是你想要检验的方差。
    $
chi_square,p_value = chi2test(sample_var = 4.9, sample_num = 24, sigma_square = 4,side='greater')

print("p值：", p_value)

p值： 0.2092362676676498

chi_square

28.175

结论：选择显著性水平 0.05 的话，P=0.2092 > 0.05, 无法拒绝原假设。具体来说就是该结果不支持方差变大的备则假设。

例：检验某考试中心升级题库后考生分数的方差是否有显著变化

某数据分析师认证考试机构CDA考试中心，历史上的持证人考试分数的方差为\(\sigma^2=100\)，现在升级了题库，该考试中心希望新型考题的方差保持在原有水平上，为了研究该问题，收集到了30份新考题的考分组成的样本，样本方差是，在的显著性水平下进行假设检验。

分析过程：由于目标是希望考试分数的方差保持原有水平，因此选择双侧检验，于是我们有了原假设和备择假设

\(H_0:\sigma^2<=100\)，\(H_1:\sigma^2\neq100\)

p_value = chi2test(sample_var = 152, sample_num = 30, sigma_square = 100,side='two-sided')

print("p值：", p_value)

p值： (44.08, 0.07213100536907469)

结论：选择显著性水平 0.05 的话，P=0.0721 > 0.05, 故无法拒绝原假设。具体来说就是不支持方差发生了变化的备则假设。

为什么two-sided和less，用的是cdf，而greater用的是sf

在统计学中，双侧检验（two-sided test）、左侧检验（less）和右侧检验（greater）的区别主要体现在对原假设的拒绝区域的选择上。这种选择涉及到累积分布函数（CDF）和生存函数（SF）的不同使用。

  • 双侧检验（two-sided test）：
    在双侧检验中，我们关心的是样本统计量在分布的两个尾部的概率。CDF（累积分布函数）用于计算累积概率，因为我们需要考虑左尾和右尾两个方向的概率。通过计算两个尾部的概率，最终得到双侧检验的 p 值。这是为什么使用 stats.chi2(df=sample_num-1).cdf(chi_square) 的原因。

  • 左侧检验（less）：
    在左侧检验中，我们关心的是样本统计量小于某个特定值的概率。因此，我们使用累积分布函数（CDF）来计算小于该值的概率。这是为什么使用 stats.chi2(df=sample_num-1).cdf(chi_square) 的原因。

  • 右侧检验（greater）：
    在右侧检验中，我们关心的是样本统计量大于某个特定值的概率。这时我们使用生存函数（SF），因为生存函数表示大于某个值的概率。这是为什么使用 stats.chi2(df=sample_num-1).sf(chi_square) 的原因。re) 的原因。re) 的原因。

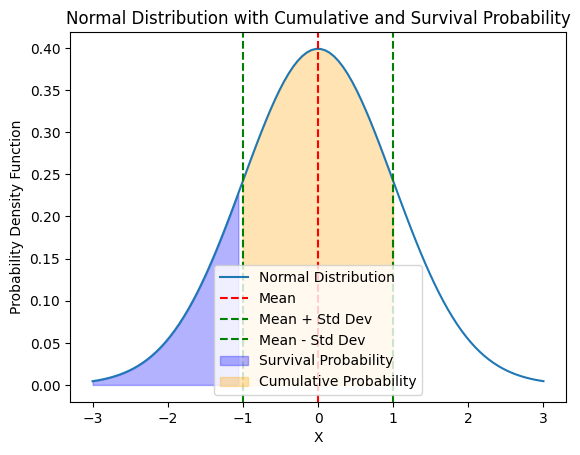
区分cdf和sf

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 创建一个正态分布
mu = 0
sigma = 1
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
y = norm.pdf(x, mu, sigma)

# 绘制正态分布曲线
plt.plot(x, y, label='Normal Distribution')

# 添加均值和标准差的标记
plt.axvline(mu, color='r', linestyle='--', label='Mean')
plt.axvline(mu + sigma, color='g', linestyle='--', label='Mean + Std Dev')
plt.axvline(mu - sigma, color='g', linestyle='--', label='Mean - Std Dev')

# 添加累积概率和生存概率的区域
plt.fill_between(x, 0, y, where=(x < mu - sigma), color='blue', alpha=0.3, label='Survival Probability')
plt.fill_between(x, 0, y, where=(x >= mu - sigma) & (x <= mu + sigma), color='orange', alpha=0.3, label='Cumulative Probability')

# 添加标签和图例
plt.title('Normal Distribution with Cumulative and Survival Probability')
plt.xlabel('X')
plt.ylabel('Probability Density Function')
plt.legend()

# 显示图形
plt.show()

png

  • 橙色区域代表累积概率。这是从分布的起点到某一特定点（比如均值加一个标准差）的概率，即在这个点之前的概率。在橙色区域下的面积表示在该特定点之前的累积概率。

  • 蓝色区域代表生存概率。这是从分布的某一特定点（比如均值减一个标准差）到分布的尽头的概率，即在这个点之后的概率。在蓝色区域下的面积表示在该特定点之后的生存概率。

cdf是什么？

对于随机变量\(X\),其累计分布函数\(F(x)\)定义为在点\(x\)处小于或等于\(x\)的概率。

\[F(x)=P(X<=x) \]

具体形式为累计概率的积分：

\[F(x)=\int_{-\infty}^{x} f(t)\,dt \]

\(其中，f(t)是X的概率密度函数。\)

sf是什么？

\(生成函数S(x)表示随机变量X大于x的概率，数学公式：\)

\[S(x)=P(X>x)=1-F(x) \]

生存函数和累计分布函数的关系是互补的，生存函数也可以表示为概率密度函数的积分：

\[S(x)=\int_{x}^{\infty} f(t)\,dt \]

pdf是什么？

PDF 代表概率密度函数（Probability Density Function），是在概率论和统计学中用来描述随机变量的概率分布的函数。对于连续型随机变量，概率密度函数是描述随机变量在某个取值附近的概率分布情况的函数。

在数学上，对于随机变量 X 的概率密度函数，可以用如下表示：

\[P(a≤X≤b)=\int_{a}^{b}​ f(x)dx\]

其中，f(x) 就是 X 的概率密度函数。

scipy.stats.chi2()

<scipy.stats._distn_infrastructure.rv_continuous_frozen at 0x1e72740da90>

两个总体的假设检验

A = [58,64,55,66,67,73,66,67,73]
B = [58,69,71,64,68,64,55,66,68]

AB_DF = pd.DataFrame([A,B]).T

AB_DF
0 1
0 58 58
1 64 69
2 55 71
3 66 64
4 67 68
5 73 64
6 66 55
7 67 66
8 73 68 
t, pval = scipy.stats.ttest_ind(AB_DF[0],AB_DF[1],alternative = 'greater')

pval

0.4024903998235948

t

0.25103723559318414

方差分析

单因素多水平方差分析

import pandas as pd
import numpy as np
from scipy import stats

# 数据
A = [58,64,55,66,67,73,66,67,73]
B = [58,69,71,64,68]
C = [48,57]

data = [A, B, C]
# 方差的齐性检验
w, p = stats.levene(*data)
if p < 0.05:
    print('方差齐性假设不成立')
 
# 成立之后， 就可以进行单因素方差分析
f_value, p_value = stats.f_oneway(*data)
# 输出结果
print("F_value:", f_value)
print("p_value:", p_value)
F_value: 9.176470588235295
p_value: 0.0038184120755124806

F_value: 4.555591218384902
p_value: 0.03167043281621416

双因素多水平方差分析

import numpy as np
import pandas as pd 

d = np.array([[58.2, 52.6, 56.2, 41.2, 65.3, 60.8],
    [49.1, 42.8, 54.1, 50.5, 51.6, 48.4],
    [60.1, 58.3, 70.9, 73.2, 39.2, 40.7],
    [75.8, 71.5, 58.2, 51.0, 48.7,41.4]
])
data = pd.DataFrame(d)
data.index=pd.Index(['A1','A2','A3','A4'],name='燃料')
data.columns=pd.Index(['B1','B1','B2','B2','B3','B3'],name='推进器')

# pandas宽表转长表
data = data.reset_index().melt(id_vars =['燃料'])
data = data.rename(columns={'value':'射程'})
data.sample(5)
燃料 推进器 射程
6 A3 B1 58.3
1 A2 B1 49.1
0 A1 B1 58.2
21 A2 B3 48.4
12 A1 B2 41.2
posted @ 2024-05-17 11:16  江雪独钓翁  阅读(4)  评论(0)  编辑  收藏  举报