Python数据分析与挖掘实战（1-3章）

非原创，仅个人关于《Python数据分析与挖掘实战》的学习笔记

第一章基础

略

第二章数据分析简介

基本概念

元组、列表、字典、集合

函数式编程：

map()函数：定义一个函数，然后用map()逐一应用到map列表中的每个元素。map(lambda x+2:a)
reduce()函数：用于递归计算。reduce(lambda x,y:x*y,range(1,n+1))

数据分析常用库

numpy 数组，高效处理函数
scipy 矩阵相关计算
matplotlib 可视化
pandas 数据分析
statsmodels 统计建模
scikit-learn 回归、分类、聚类等机器学习
keras 深度学习，建立神经网络及深度学习模型
gensim 文本主题模型，文本挖掘

第三章数据探索

3.1 数据质量分析

缺失值分析
异常值

import pandas as pd
from scipy import stats

# 读取CSV文件
data = pd.read_csv(f'E:\中经社\中资美元债\PVR\CEIS_Corps_Pricing_Liquidity_20240409.csv')

# 假设我们对数值型数据进行异常值检测，这里以'amountOutstanding'列为例
# 首先，确保数据是数值型的
data['amountOutstanding'] = pd.to_numeric(data['amountOutstanding'], errors='coerce')

# 计算Z-score
z_scores = stats.zscore(data['amountOutstanding'])

# 找出Z-score的绝对值大于1的点作为异常值
threshold = 1
abs_z_scores = abs(z_scores)
anomaly_indices = abs_z_scores > threshold

# 标记异常值
data['anomaly'] = False
data.loc[anomaly_indices, 'anomaly'] = True

# 显示含有异常值的行
data[data['anomaly']]

	priceAsOf	name	isin	cusip	shortName	ticker	amountOutstanding	classification	bondType	bondSubType	...	liquidityScore30DayCount	liquidityScore60Day	liquidityScore60DayCount	liquidityScore90Day	liquidityScore90DayCount	quotesCount1Day	quotesCount10Day	quotesDealerCount1Day	quotesDealerCount10Day	anomaly
0	2024-04-09	GS1600	XS2446005907	Y3991YRL9	Indl & Coml Bk China Ltd Hong Kong	UNBKHK	1200000000	Financials	Fixed	Fixed	...	22	1	42	1	64	112	90	16	13	True
1	2024-04-09	GS1600	USG7801RAE92	G7801RAE9	Sands China Ltd	SANDCHI	3062000	Consumer Services	Stepup	FixedStep	...	22	1	42	1	64	228	169	20	14	True
2	2024-04-09	GS1600	USG7801RAD10	G7801RAD1	Sands China Ltd	SANDCHI	2625000	Consumer Services	Stepup	FixedStep	...	22	1	42	1	64	201	168	20	14	True
9	2024-04-09	GS1600	US00131MAJ27	00131MAJ2	AIA Group Ltd	AIAGRO	1000000000	Financials	Fixed	Fixed	...	22	1	42	1	64	368	275	23	17	True
10	2024-04-09	GS1600	US00131LAJ44	00131LAJ4	AIA Group Ltd	AIAGRO	1000000000	Financials	Fixed	Fixed	...	22	1	42	1	64	350	256	22	16	True
16	2024-04-09	GS1600	XS2384565508	Y3969JAU8	INDL COML BK OF CHINA LTD SINGAPORE BRH	INDUANBE	1050000000	Financials	Fixed	Fixed	...	22	1	42	1	64	106	88	13	11	True

6 rows × 169 columns

箱型图异常值检测

import pandas as pd
import matplotlib.pyplot as plt
# 解决中文乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 请确保您的文件路径是正确的
file_path = r'E:\中经社\中资美元债\PVR\CEIS_Corps_Pricing_Liquidity_20240409.csv'

# 读取CSV文件
data = pd.read_csv(file_path)

# 选择'bidPrice'列数据进行箱型图绘制，并确保数据是数值型的
data['bidPrice'] = pd.to_numeric(data['bidPrice'], errors='coerce')

# 计算箱线图的统计数据，quantile()样本分位数 (不同 % 的值)
Q1 = data['bidPrice'].quantile(0.25)
Q3 = data['bidPrice'].quantile(0.75)
IQR = Q3 - Q1

# 计算异常值的阈值
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 过滤出数据中的异常值
outliers = data[(data['bidPrice'] < lower_bound) | (data['bidPrice'] > upper_bound)]

# 绘制箱线图
plt.figure(figsize=(10, 6))  # 设置图表的大小

# 绘制箱型图，这里notch=True表示带有凹槽的箱型图，vert=True表示垂直箱型图
box = plt.boxplot(data['bidPrice'], notch=True, vert=True)

# 添加异常值标记
plt.plot([1]*len(outliers), outliers['bidPrice'], 'ro', markersize=5) 

# 设置标题和轴标签
plt.title('异常值检测箱型图分析')
plt.xlabel('Bid Price')

# 由于只有一个箱体，我们将X轴的刻度和标签设置为一个点，以避免混淆
plt.xticks([1])

# 显示图表
plt.show()

不一致的值
重复数据及含有特殊符号的数据

3.2 数据特征分析

3.2.1 分布分析

3.2.1.1 定量

从df中提取销售额数据

# 方法1：

sales = df['销售额（元）']

# 绘制直方图
plt.hist(sales, bins=10, edgecolor='black')

# 添加标题和标签
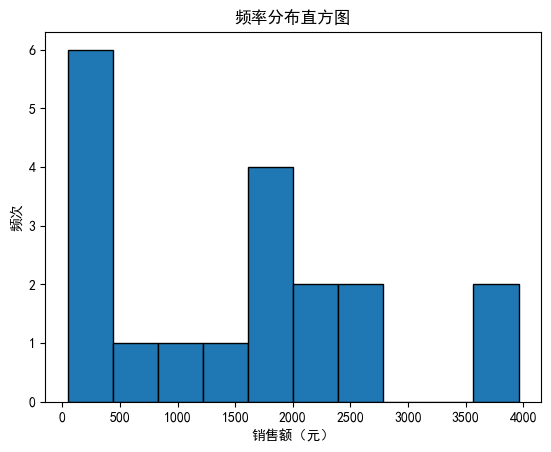
plt.title('频率分布直方图')
plt.xlabel('销售额（元）')
plt.ylabel('频次')

# 显示图形
plt.show()

# 方法2：

import matplotlib.pyplot as plt
import numpy as np
# 从df中提取销售额数据
sales = df['销售额（元）']

# 计算频率分布
values, base = np.histogram(sales, bins=10, density=True)

# 计算直方图的宽度，即每个bin的宽度
width = (df['销售额（元）'].max() - df['销售额（元）'].min()) / 10

# 计算直方图的中心点
center = (base[1:] + base[:-1]) * 0.5

# 绘制直方图
plt.bar(center, values, width=width, label='频率分布', edgecolor='black')

# 添加标题和标签
plt.title('频率分布直方图')
plt.xlabel('销售额（元）')
plt.ylabel('频率')

# 显示图例
plt.legend()

# 显示图形
plt.show()

3.2.1.2 定性

常常采用饼图和条形图来描述。

3.2.2 对比分析

绝对比较
相对比较

3.2.3 统计量分析

3.2.3.1 集中趋势度量

均值
中位数
众数

3.2.3.1 离中趋势度量

极差

statistics = sales.describe()

statistics

count      19.000000
mean     1496.684211
std      1198.271211
min        45.000000
25%       420.000000
50%      1710.000000
75%      2220.000000
max      3960.000000
Name: 销售额（元）, dtype: float64

\[极差=max-min \]

statistics.loc['range'] = statistics.loc['max']-statistics.loc['min']

标准差

\[s=\sqrt \frac{\sum(x_i-\overline x)^2}{n} \]

变异系数

\[CV=\frac{s}{\overline x}\times 100\% \]

statistics.loc['var'] = statistics.loc['std']-statistics.loc['mean']

四分位数区距

statistics.loc['dis'] = statistics.loc['75%']-statistics.loc['25%']

statistics

count      19.000000
mean     1496.684211
std      1198.271211
min        45.000000
25%       420.000000
50%      1710.000000
75%      2220.000000
max      3960.000000
range    3915.000000
var      -298.413000
dis      1800.000000
Name: 销售额（元）, dtype: float64

3.2.4 周期性分析

时序图

3.2.5 贡献度分析

from io import StringIO
# 假设数据已经被转换成了CSV格式的字符串
data_csv = """id,mame,profit
17148,Al,9173
17154,A2,5729
109,A3,4811
117,A4,3594
17151,AS,3195
14,A6,3026
2868,A7,2378
397,A8,1970
88,A9,1877
426,A10,1782"""

# 使用StringIO来创建一个字符串流
data_csv_df = pd.read_csv(StringIO(data_csv))

# 显示DataFrame
data_csv_df

	id	mame	profit
0	17148	Al	9173
1	17154	A2	5729
2	109	A3	4811
3	117	A4	3594
4	17151	AS	3195
5	14	A6	3026
6	2868	A7	2378
7	397	A8	1970
8	88	A9	1877
9	426	A10	1782

通过分析，做出增加对哪些菜品的成本投入。

data_csv_df = data_csv_df['profit'].copy()

data_csv_df.sort_values (ascending = False)

0    9173
1    5729
2    4811
3    3594
4    3195
5    3026
6    2378
7    1970
8    1877
9    1782
Name: profit, dtype: int64

import matplotlib.pyplot as plt

# 创建图形并绘制柱状图
plt.figure()
data_csv_df.plot(kind='bar')
plt.ylabel('盈利')  # 设置主 y 轴的标签

# 计算累计和并绘制
p = 1.0 * data_csv_df.cumsum() / data_csv_df.sum()
p.plot(color='r', secondary_y=True, style='-o', linewidth=2)
# 设置次 y 轴的标签，并指定颜色
plt.ylabel('盈利（比例）', color='r')

# 选择要注释的数据点
# 假设我们注释第七个数据点
value_to_annotate = p.iloc[6]

# 格式化数据点的值
formatted_value = format(value_to_annotate, '.4%')

# 添加注释
plt.annotate(
    formatted_value,  # 注释的文本
    xy=(p.index[6], value_to_annotate),  # 注释文本的起始点 (x, y)
    xytext=(0, 20),  # 注释文本的结束点 (x, y)，根据实际情况调整
    textcoords='offset points',  # 指定注释文本的坐标系统
    arrowprops=dict(
        arrowstyle="->",  # 箭头样式
        connectionstyle="arc3,rad=.2"  # 连接样式
    ),
    color='r'  # 注释文本颜色与线颜色相同
)

# 显示图形
plt.show()

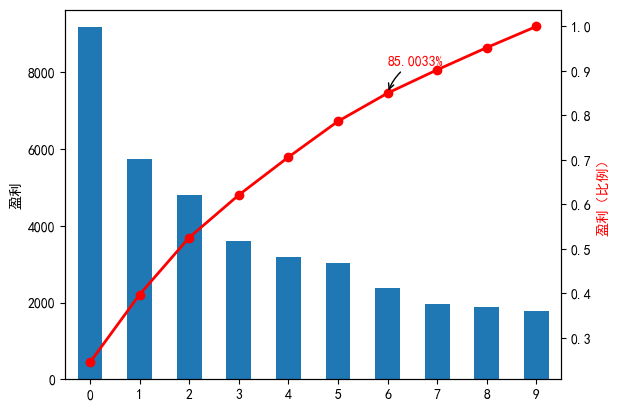
<b结论：

A1~A7 这7个菜品，占菜品种类数的70%，总盈利占总盈利额的85.0003%

3.2.6 相关性分析

3.2.6.1 直接绘制散点图

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
np.random.seed(0)
x = np.random.rand(100)  # 第一个变量
y = 2 * x + np.random.normal(0, 0.1, 100)  # 第二个变量与第一个变量存在线性关系，并加入一些噪声
# y = 2 * x**2 + np.random.normal(0, 0.1, 100)  # 第二个变量与第一个变量存在非线性关系，并加入一些噪声
# y = -2 * x + np.random.normal(0, 0.1, 100)  # 第二个变量与第一个变量存在负线性关系，并加入一些噪声

# 绘制散点图
plt.scatter(x, y, color='blue', label='Data Points')

# 计算相关系数
correlation = np.corrcoef(x, y)[0, 1]

# 添加标题和标签
plt.title('2个变量的相关性分析')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()

# # 添加相关系数标注
# plt.annotate(f'Correlation: {correlation:.2f}', xy=(0.05, 0.95), xycoords='axes fraction', fontsize=10, ha='left', va='top', bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5))

# 显示图形
plt.show()

3.2.6.2 绘制散点图矩阵

import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings

# 忽略警告
warnings.filterwarnings("ignore")

# 生成一些示例数据
np.random.seed(0)
data = pd.DataFrame(np.random.randn(100, 4), columns=['A', 'B', 'C', 'D'])

# 添加非线性相关关系
data['B'] = data['A'] + np.random.normal(0, 1, 100)
data['C'] = 2 * data['A'] + np.random.normal(0, 2, 100)
data['D'] = -3 * data['A'] + np.random.normal(0, 3, 100)

# 将无穷大值替换为NaN
data.replace([np.inf, -np.inf], np.nan, inplace=True)

# 绘制散点图矩阵
sns.pairplot(data)
plt.show()

3.2.6.3 计算相关系数

皮尔逊相关

import numpy as np

# 生成示例数据
np.random.seed(0)
x = np.random.rand(100)  # 生成100个在[0,1)之间的随机数
y = 2 * x + np.random.normal(0, 0.1, 100)  # y与x存在线性关系，并加入一些噪声

# 使用NumPy计算Pearson相关系数
correlation = np.corrcoef(x, y)[0, 1]

print("Pearson相关系数:", correlation)
print("p_value:", p_value)

Pearson相关系数: 0.9853103832101714
p_value: 5.4168015521507496e-42

斯皮尔曼相关

import numpy as np
from scipy.stats import spearmanr

# 生成示例数据
np.random.seed(0)
x = np.random.rand(100)  # 生成100个在[0,1)之间的随机数
y = x**2 + np.random.normal(0, 0.1, 100)  # y与x存在非线性关系，并加入一些噪声

# 使用SciPy计算Spearman相关系数
correlation, p_value = spearmanr(x, y)

print("Spearman相关系数:", correlation)
print("p_value:", p_value)

Spearman相关系数: 0.9213201320132012
p_value: 5.4168015521507496e-42

import numpy as np
from scipy.stats import spearmanr

# 生成示例数据
np.random.seed(0)
x = np.random.rand(100)  # 生成100个在[0,1)之间的随机数
y = x**2 + np.random.normal(0, 0.1, 100)  # y与x存在非线性关系，并加入一些噪声

# 使用SciPy计算Spearman相关系数
correlation, p_value = spearmanr(x, y)

print("Spearman相关系数:", correlation)
print("p-value:", p_value)

# 判断相关系数是否显著
alpha = 0.05
if p_value < alpha:
    print("Spearman相关系数显著")
else:
    print("Spearman相关系数不显著")

Spearman相关系数: 0.9213201320132012
p-value: 5.4168015521507496e-42
Spearman相关系数显著

p-value（P值）

p-value（P值）是用于评估在零假设成立的情况下，观察到的统计量或更极端情况的概率。在统计学中，零假设通常是指两个变量之间不存在任何关系，或者另一种说法是它们之间的关系是随机的。

在Spearman相关系数的情境下，p-value可以用来判断样本数据中的Spearman相关系数是否显著。具体来说：

如果p-value小于给定的显著性水平（通常设为0.05），则我们拒绝零假设，即我们认为观察到的Spearman相关系数不是由随机性导致的，而是由于真实的相关性。
如果p-value大于显著性水平，则我们接受零假设，即我们认为观察到的Spearman相关系数可能是由随机性引起的，而不是真实的相关性。

import numpy as np
from scipy.stats import spearmanr

# 生成示例数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([3434, 2343, 4234, 125,56])

# 使用SciPy计算Spearman相关系数
correlation, p_value = spearmanr(x, y)

print("Spearman相关系数:", correlation)
print("p-value:", p_value)

# 判断相关系数是否显著
alpha = 0.05
if p_value < alpha:
    print("Spearman相关系数显著")
else:
    print("Spearman相关系数不显著")

Spearman相关系数: -0.7
p-value: 0.1881204043741873
Spearman相关系数不显著

继续介绍案例：

# 菜品名称
dishes = ['百合酱蒸凤爪', '翡翠蒸香茜饺', '金银蒜汁蒸排骨', '乐膳真味鸡', '蜜汁焗餐包', '生炒菜心', '铁板酸菜豆腐', '香煎韭菜饺', '香煎萝卜糕', '原汁原味菜心']

# 日期
dates = ['2015/1/1', '2015/1/2', '2015/1/3', '2015/1/4', '2015/1/5', '2015/1/6']

# 销量数据，每个列表中的数字对应相应菜品在对应日期的销量
sales_data = [
    [17, 6, 8, 24, 13, 13, 18, 10, 10, 27],
    [11, 15, 14, 13, 9, 10, 19, 13, 14, 13],
    [10, 8, 12, 13, 8, 3, 7, 11, 10, 9],
    [9, 6, 6, 3, 10, 9, 9, 13, 14, 13],
    [4, 10, 13, 0, 12, 10, 17, 11, 13, 14],
    [13, 10, 13, 16, 8, 9, 12, 11, 5, 9]
]

# 创建DataFrame
sales_data_df = pd.DataFrame(sales_data, index=dates, columns=dishes)

sales_data_df

	百合酱蒸凤爪	翡翠蒸香茜饺	金银蒜汁蒸排骨	乐膳真味鸡	蜜汁焗餐包	生炒菜心	铁板酸菜豆腐	香煎韭菜饺	香煎萝卜糕	原汁原味菜心
2015/1/1	17	6	8	24	13	13	18	10	10	27
2015/1/2	11	15	14	13	9	10	19	13	14	13
2015/1/3	10	8	12	13	8	3	7	11	10	9
2015/1/4	9	6	6	3	10	9	9	13	14	13
2015/1/5	4	10	13	0	12	10	17	11	13	14
2015/1/6	13	10	13	16	8	9	12	11	5	9

# 计算Spearman相关系数
spearman_corr = sales_data_df.corr(method='spearman')
spearman_corr

	百合酱蒸凤爪	翡翠蒸香茜饺	金银蒜汁蒸排骨	乐膳真味鸡	蜜汁焗餐包	生炒菜心	铁板酸菜豆腐	香煎韭菜饺	香煎萝卜糕	原汁原味菜心
百合酱蒸凤爪	1.000000	-0.088273	0.028989	0.985611	-0.028989	0.323669	0.371429	-0.462910	-0.529641	0.029424
翡翠蒸香茜饺	-0.088273	1.000000	0.985184	-0.179124	-0.403030	0.045455	0.441367	0.333712	0.090909	-0.272727
金银蒜汁蒸排骨	0.028989	0.985184	1.000000	-0.058824	-0.338235	0.149270	0.521794	0.187867	0.000000	-0.194051
乐膳真味鸡	0.985611	-0.179124	-0.058824	1.000000	-0.073529	0.223906	0.231908	-0.547946	-0.626936	-0.029854
蜜汁焗餐包	-0.028989	-0.403030	-0.338235	-0.073529	1.000000	0.820987	0.492805	-0.313112	0.313468	0.985184
生炒菜心	0.323669	0.045455	0.149270	0.223906	0.820987	1.000000	0.882735	-0.317821	0.181818	0.893939
铁板酸菜豆腐	0.371429	0.441367	0.521794	0.231908	0.492805	0.882735	1.000000	-0.030861	0.264820	0.617914
香煎韭菜饺	-0.462910	0.333712	0.187867	-0.547946	-0.313112	-0.317821	-0.030861	1.000000	0.762770	-0.317821
香煎萝卜糕	-0.529641	0.090909	0.000000	-0.626936	0.313468	0.181818	0.264820	0.762770	1.000000	0.318182
原汁原味菜心	0.029424	-0.272727	-0.194051	-0.029854	0.985184	0.893939	0.617914	-0.317821	0.318182	1.000000

spearman_corr['百合酱蒸凤爪']

百合酱蒸凤爪     1.000000
翡翠蒸香茜饺    -0.088273
金银蒜汁蒸排骨    0.028989
乐膳真味鸡      0.985611
蜜汁焗餐包     -0.028989
生炒菜心       0.323669
铁板酸菜豆腐     0.371429
香煎韭菜饺     -0.462910
香煎萝卜糕     -0.529641
原汁原味菜心     0.029424
Name: 百合酱蒸凤爪, dtype: float64

结论：

相关系数越接近1，表示相关性更大，越接近0，则表示无相关性，如果是负数，则更加无相关性。

# 计算Pearson相关系数
Pearson_corr = sales_data_df.corr()
Pearson_corr

	百合酱蒸凤爪	翡翠蒸香茜饺	金银蒜汁蒸排骨	乐膳真味鸡	蜜汁焗餐包	生炒菜心	铁板酸菜豆腐	香煎韭菜饺	香煎萝卜糕	原汁原味菜心
百合酱蒸凤爪	1.000000	-0.215108	-0.272730	0.948947	0.044137	0.323976	0.140652	-0.340168	-0.494433	0.524731
翡翠蒸香茜饺	-0.215108	1.000000	0.827769	-0.077693	-0.367647	0.018051	0.485879	0.411706	0.154122	-0.376388
金银蒜汁蒸排骨	-0.272730	0.827769	1.000000	-0.021189	-0.413919	-0.245327	0.282654	-0.050637	-0.214834	-0.485254
乐膳真味鸡	0.948947	-0.077693	-0.021189	1.000000	0.010859	0.214859	0.207623	-0.492837	-0.558896	0.478112
蜜汁焗餐包	0.044137	-0.367647	-0.413919	0.010859	1.000000	0.725324	0.585705	-0.389249	0.330289	0.860811
生炒菜心	0.323976	0.018051	-0.245327	0.214859	0.725324	1.000000	0.795932	-0.099381	0.122977	0.741747
铁板酸菜豆腐	0.140652	0.485879	0.282654	0.207623	0.585705	0.795932	1.000000	-0.097078	0.240255	0.580441
香煎韭菜饺	-0.340168	0.411706	-0.050637	-0.492837	-0.389249	-0.099381	-0.097078	1.000000	0.612826	-0.430007
香煎萝卜糕	-0.494433	0.154122	-0.214834	-0.558896	0.330289	0.122977	0.240255	0.612826	1.000000	0.138999
原汁原味菜心	0.524731	-0.376388	-0.485254	0.478112	0.860811	0.741747	0.580441	-0.430007	0.138999	1.000000

3.2 Python主要数据探索函数

数据探索的库主要是Pandas和Matplotlib。

常用统计特征函数：

sum() 计算数据样本的总和
mean() 计算数据样本的算术平均数
var() 计算数据样本的方差
std() 计算数据样本的标准差
corr() 计算数据样本的Spearman(Pearson)相关系数矩阵
cov() 计算数据样本的协方差矩阵
skew() 计算数据样本值的偏度（三阶矩）
kurt() 计算数据样本值的偏度（四阶矩）
describe() 给出样本的基本描述

拓展统计特征函数：

cumsum() 依次给出前1、2、3...、n个数的和
cumprod() 依次给出前1、2、3...、n个数的积
cummax() 依次给出前1、2、3...、n个数的最大值
cummin() 依次给出前1、2、3...、n个数的最小值
rolling_window.sum()
rolling_window.mean()
rolling_window.var()
rolling_window.std()
rolling_window.corr()
rolling_window.cov()
rolling_window.skew()
rolling_window.kurt()

rolling_window.sum()

import pandas as pd

# 假设我们有一个DataFrame，其中包含了按日期索引的时间序列数据
data = {
    'date': pd.date_range(start='2021-01-01', periods=5, freq='D'),
    'value': [1, 2, 3, 4, 5]
}
df = pd.DataFrame(data).set_index('date')

# 计算窗口大小为2的滚动求和,依次对相邻两项求和
rolling_window = df['value'].rolling(window=2)
rolling_sum = rolling_window.sum()

rolling_sum

date
2021-01-01    NaN
2021-01-02    3.0
2021-01-03    5.0
2021-01-04    7.0
2021-01-05    9.0
Name: value, dtype: float64

统计作图函数：

plot() 折线图
pie() 饼图
hist() 直方图
boxplot() 箱型图
plot(logy=True) 绘制y轴的对数图形
plot(yerr=error) 绘制误差条形图

plot(yerr=error)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 生成一个随机误差数组
error = np.abs(np.random.randn(10))  # 确保误差为正值

# 生成一个正弦波形的Series
y = pd.Series(np.sin(np.arange(10)))

# 使用plot方法绘制正弦波形图
plt.plot(y.index, y, '-o')  # 使用 '-o' 格式，表示用线段和圆点绘制

# 使用errorbar添加误差条
plt.errorbar(y.index, y, yerr=error, fmt='none', ecolor='red', capsize=5)

# 显示图表
plt.show()

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 生成一个随机误差矩阵，其形状与DataFrame的列数相同
error = np.abs(np.random.randn(10, 2))  # 假设DataFrame有两列

# 生成一个包含正弦和余弦值的DataFrame
x = np.arange(10)
data = pd.DataFrame({
    'sin': np.sin(x),
    'cos': np.cos(x)
})

# 设置绘图参数
plt.figure(figsize=(10, 6))

# 为DataFrame的每一列绘制带有误差条的线
for column in data.columns:
    plt.errorbar(x, data[column], yerr=error[:, data.columns.get_loc(column)], 
                 fmt='-o', label=column, capsize=5)

# 添加图例
plt.legend()

# 显示图表
plt.show()

案例：股票收益率的波动性分析

假设你是一位金融分析师，正在研究某科技公司股票的历史表现，并希望评估其收益率的波动性。你收集了该公司过去一年内每个交易日的收盘价，并计算了每日的收益率。为了更直观地展示这些数据，你决定使用误差条形图。

步骤：

数据收集：收集过去一年内，每个交易日的收盘价。
计算收益率：计算每个交易日的收益率。收益率可以通过以下公式计算：
\(收益率=\frac{今日收盘价−昨日收盘价}{昨日收盘价}\)
计算统计量：计算收益率的均值、标准差等统计量。
绘制误差条形图：使用误差条形图展示每日收益率的分布情况，误差条表示标准差。

import pandas as pd
import matplotlib.pyplot as plt

# 假设dataframe 'df' 包含过去一年每个交易日的收盘价
df = pd.read_excel(f'D:/Notebook/excel/300059_close.xls')
df = df[0:100]
# 计算每日收益率
df['return'] = df['close'].pct_change()

# 计算每日收益率的均值和标准差
mean_return = df['return'].mean()
std_return = df['return'].std()

# 绘制误差条形图
plt.figure(figsize=(20, 6))
plt.errorbar(df.index, df['return'], yerr=std_return, fmt='none', ecolor='gray', capsize=5)
plt.axhline(y=mean_return, color='r', linestyle='--', label='收益率的均值')

plt.title('带有标准差误差条的每日股票收益率图')
plt.xlabel('交易日')
plt.ylabel('收益率')
plt.legend()
plt.show()

df

	date	close	return
0	2010-03-19	0.720866	NaN
1	2010-03-22	0.793014	0.100086
2	2010-03-23	0.804256	0.014177
3	2010-03-24	0.848608	0.055146
4	2010-03-25	0.862074	0.015868
...	...	...	...
95	2010-08-10	0.669737	-0.051966
96	2010-08-11	0.675566	0.008704
97	2010-08-12	0.664776	-0.015972
98	2010-08-13	0.680031	0.022948
99	2010-08-16	0.692434	0.018238

100 rows × 3 columns

均值：

表示收益率的平均水平，可以作为评估股票长期表现的一个指标。

误差条：

表示收益率的波动性。较长的误差条表明在某些交易日，股票的收益波动较大，这可能意味着较高的风险。

posted @ 2024-05-17 09:27 江雪独钓翁阅读(9) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Loading

江雪独钓翁

Python数据分析与挖掘实战（1-3章）

第一章基础

第二章数据分析简介

元组、列表、字典、集合

函数式编程：

第三章数据探索

3.1 数据质量分析

箱型图异常值检测

3.2 数据特征分析

3.2.1 分布分析

3.2.1.1 定量

从df中提取销售额数据

3.2.1.2 定性

3.2.2 对比分析

3.2.3 统计量分析

3.2.3.1 集中趋势度量

3.2.3.1 离中趋势度量

3.2.4 周期性分析

3.2.5 贡献度分析

3.2.6 相关性分析

3.2.6.1 直接绘制散点图

3.2.6.2 绘制散点图矩阵

3.2.6.3 计算相关系数

皮尔逊相关

斯皮尔曼相关

3.2 Python主要数据探索函数

常用统计特征函数：

拓展统计特征函数：

rolling_window.sum()

统计作图函数：

plot(yerr=error)

案例：股票收益率的波动性分析

公告

Loading

江雪独钓翁

Python数据分析与挖掘实战（1-3章）

第一章 基础

第二章 数据分析简介

元组、列表、字典、集合

函数式编程：

第三章 数据探索

3.1 数据质量分析

箱型图异常值检测

3.2 数据特征分析

3.2.1 分布分析

3.2.1.1 定量

从df中提取销售额数据

3.2.1.2 定性

3.2.2 对比分析

3.2.3 统计量分析

3.2.3.1 集中趋势度量

3.2.3.1 离中趋势度量

3.2.4 周期性分析

3.2.5 贡献度分析

3.2.6 相关性分析

3.2.6.1 直接绘制散点图

3.2.6.2 绘制散点图矩阵

3.2.6.3 计算相关系数

皮尔逊相关

斯皮尔曼相关

3.2 Python主要数据探索函数

常用统计特征函数：

拓展统计特征函数：

rolling_window.sum()

统计作图函数：

plot(yerr=error)

案例：股票收益率的波动性分析

公告

第一章基础

第二章数据分析简介

第三章数据探索