递推--2

例一：诸侯安置

题目描述

很久以前，有一个强大的帝国，它的国土成正方形状，如图所示。

这个国家有若干诸侯。由于这些诸侯都曾立下赫赫战功，国王准备给他们每人一块封地(正方形中的一格)。但是，这些诸侯又非常好战，当两个诸侯位于同一行或同一列时，他们就会开战。如下图2—3为n＝3时的国土，阴影部分表示诸侯所处的位置。前两幅图中的诸侯可以互相攻击，第三幅则不可以。

国王自然不愿意看到他的诸侯们互相开战，致使国家动荡不安。 因此，他希望通过合理的安排诸侯所处的位置，使他们两两之间都不能攻击。

现在，给出正方形的边长n，以及需要封地的诸侯数量k，要求你求出所有可能的安置方案数。(n≤l00，k≤2n2-2n+1)

由于方案数可能很多，你只需要输出方案数除以504的余数即可。

输入格式

仅一行，两个整数n和k，中间用一空格隔开。

输出格式

一个整数，表示方案数除以504的余数。

输入输出样例

输入 #1复制

2 2

输出 #1复制

4

说明/提示

注意：镜面和旋转的情况属于不同的方案。

---

 

#include<iostream>
#include<cstdio>
using namespace std;
int f[1000][1000],len[1000]; //f[i][j]表示前j列放了k个诸侯 ，len[i]表示第i列有几行 
int main()
{
    int n,k;
    cin>>n>>k;
    
    if(k==0)
    {
        cout<<1;
        return 0;
    }
    
    if(k>=n*n-1)
    {
        cout<<0;
        return 0;
    }                      //特判 （几个测试点很坑啊） 
    
    for(int i=1;i<n;i++) 
    len[2*i-1]=len[2*i]=2*i-1;    //找规律，把每一列的行数都算出来 
    
    len[2*n-1]=2*n-1;    //因为最后一行是单独的，所以单独判断 
    
    for(int i=1;i<=2*n-1;i++)
      f[i][1]=f[i-1][1]+len[i];        //初始化设置边界：前i列只放置一个诸侯的分法应该是前i列所有的格子数 
    for(int i=1;i<=2*n-1;i++)
     for(int k=2;k<=2*n-1;k++)
      {
          f[i][k]=f[i-1][k]+f[i-1][k-1]*(len[i]-k+1);  //前j列放了k个诸侯的分法=这一列不放置诸侯的情况+这一列放诸侯的情况（乘法计数原理） 
          f[i][k]%=504;   // %%%
      }
    cout<<f[2*n-1][k];  //最后一列放置K个诸侯即为答案 
    return 0;
} 

 思路： 把国土的右半部分移到左边，这样既满足了动态规划的无后效性，又不会影响结果

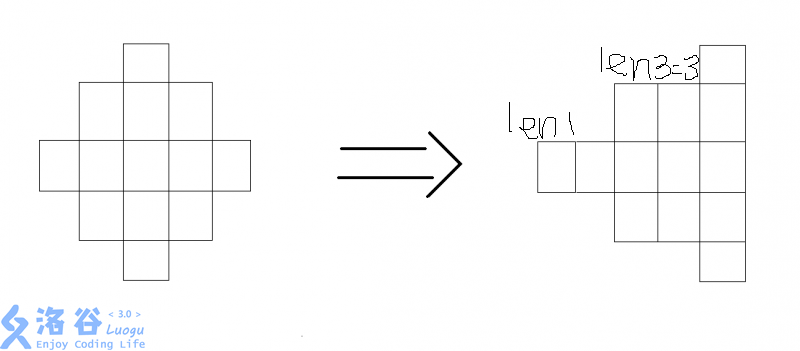
 why：因为国土形状不是呈单调递增或递减的，不好递推，所以应该让它有规律

1.  通过规律计算出每一列的行数
2. 设置边界：当前 i 列只放一个诸侯的时候是什么情况......
3. 从而递推前 i 列放置 j 个诸侯的情况 = 这一列不放诸侯 + 这一列放诸侯（这一列没有诸侯占领的每一行都有可能放，所以相 * ）

---

 

 例二：矩形

题目描述

给出一个 n * n 的矩阵，矩阵中，有些格子被染成白色，有些格子被染成黑色，现要求矩阵中白色矩形的数量

输入格式

第一行，一个整数nn，表示矩形的大小。

接下来nn行，每行nn个字符，这些字符为“WW”或“BB”。其中“WW”表示白格，“BB”表示黑格。

输出格式

一个正整数，为白色矩形数量

输入输出样例

输入 #1复制

4
WWBW
BBWB
WBWW
WBWB

输出 #1复制

15

#include<iostream>
#include<cstdio>
using namespace std;  
int a[1000];
char ch;
int main()
{
    int n,now,ans=0;
    cin>>n;
    for(int i=1;i<=n;i++)
     {
       for(int j=1;j<=n;j++)
      {
          cin>>ch;
          if(ch=='W') ++a[j];
          else a[j]=0;
      }                  //先输完一行
      for(int j=1;j<=n;j++)
       {
           now=a[j];
           for(int k=j;k<=n;k++)
           {
               if(a[k]==0) break;  //如果a[k]==0，说明这个格子就是黑色的，所以不能连续，形成大白格子
               else 
               {
                   now=min(now,a[k]); //应该取有最少的连续白格子的数量
                   ans+=now;
            }
        }
       }
     }
    cout<<ans;
    return 0;
}

原题解及图示：https://www.luogu.com.cn/problem/solution/P1191

思路：边输边解。（i，j） 表示从（ i , j ）点为终点，以之前某一行为黑格子的坐标为起点，向右一直到（ i , k ），此时宽度下有多少个白格子。设置 a [ i ] 数组表示在当前这一行每一列有多少个连续的白格子