基础--递推
递推:
递推学不好,动规做不了
基本思路:
确定状态转移方程:从第 i-1 位怎么转移到第 i 位 (找规律)
例题:
例一:骨牌
有 2*n 的一个长方形方格,用一个1*2 的骨牌铺满方格。求输入一个 n ,最多有多少种铺法(n = 3 ,有如下图三种铺法)

基本思路:用递推方法找规律
- 当 n=1 时,只有一种铺法
- 当 n=2 时,有两种铺法(可以并列竖排,可以并列横排)
- 当 n=3 时,有三种铺法(如上图)
推出规律:对一般的 n 来说,第一个骨牌有两种放置情况
- 横着放,占两格
- 竖着放,占一格
若第一个骨牌是横着放,则需要对剩下的 n-2 进行排列,此时方法为f(n-2)个
若第一个骨牌是竖着放,则需要对剩下的 n-1 进行排列,此时方法为f(n-1)个
所以,递推式为 f(n)=f(n-1)+f(n-2)
1 f[1]=1,f[2]=2; 2 for(int i=3;i<=n;i++) 3 f[i]=f[i-1]+f[i-2]; 4 cout<<f[n]; 5 return 0;
例二:昆虫繁殖
有一种昆虫,每过x个月产y对卵,每对卵需要2个月才能长成成虫。假设每对成虫不死,并且每对卵刚张成成虫的第一个月不产卵(过x个月产卵)。第一个月只有一对成虫,问z个月后有多少对成虫?
输入一行三个数,分别为x,y,z。x≤20,1≤y≤20,z≤50。
Example Input
1 2 8
Example Output
37
1 #include<bits/stdc++.h> 2 using namespace std; 3 int a[1000],b[1000]; //a[i]为老虫子的个数,b[i]为小虫子的个数 4 int main() 5 { 6 int x,y,z; 7 cin>>x>>y>>z; 8 for(int i=1;i<=x;i++) 9 a[i]=1; //在前x个月里只有一对老虫子(还没生出小虫子) 10 for(int i=x+1;i<=z+1;i++) 11 { 12 b[i]=y*a[i-x]; //这个月生出了多少对小虫子 13 a[i]=a[i-1]+b[i-2]; //现在这个月的老虫子数量=上个月的老虫子数量+上上个月的小虫子数量(已经长大了) 14 } 15 cout<<a[z+1]; //求的是现在一共有多少对老虫子,如果求总共有多少对虫子应该是a[z+1]+b[z+1]; 16 return 0; 17 }
思路:用数组 a[ i ] 代表第 i 个月的老虫子数量,用数组 b[ i ] 表示第 i 个月的小虫子的数量 模拟递推求解
(如果每隔k个月老虫子会死怎么算) a[ i ] - = a[ i-k ] ?
例三:位数问题
问题描述:在所有的n位数中,有多少个数中有偶数个数字3?由于结果很大,你只需要输出对这个答案对12345取余的值
输入格式:输入一个数字n
输出格式:输出有多少个数中有偶数个数字3
输入样例:2
输出样例:73
数据范围:1<=n<=1000
1 #include<bits/stdc++.h> 2 using namespace std; 3 int f[1000][2]; //f[i][0]表示前i位数有偶数个3的有几种情况,f[i][1]表示有奇数个三的有几种情况 4 int main() 5 { 6 int n; 7 cin>>n; 8 f[1][0]=9; // 0 1 2 4 5 6 7 8 9 有0个3 9 f[1][1]=1; // 3 10 for(int i=2;i<=n;i++) 11 { 12 int x=f[i-1][0]; 13 if(i==n) x--; //因为第一位数可能是0,所以先让第一位可以是0,最后一位再不取0(这样最后一位就少了0这种情况,所以X--),相当于倒过来; 14 f[i][0]=f[i-1][0]*x+f[i-1][1]; 15 f[i][1]=f[i-1][1]*x+f[i-1][0]; 16 } 17 cout<<f[n][0]; 18 return 0; 19 }
思路:递推 从第 n-1 位推到第 n 位
原来 n-1 位有偶数个3,再加上的一位有9种可能(0,1,2,4,5,6,7...)原来 n-1 位有奇数个3,再加上的一位只有1种可能(3),变成偶数个3
所以递推式为:f [ i ] [ 0 ] = f [ i - 1 ] [ 0 ] *9 + f [ i - 1 ] [ 1 ]
例四:过河卒问题
棋盘上 AA 点有一个过河卒,需要走到目标 BB 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 CC 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,AA 点 (0, 0)(0,0)、BB 点 (n, m)(n,m),同样马的位置坐标是需要给出的。
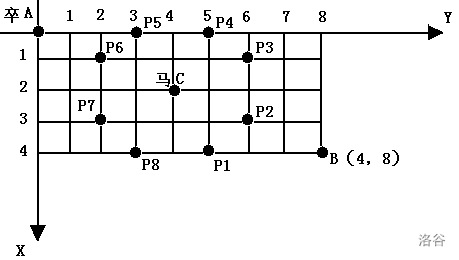
现在要求你计算出卒从 AA 点能够到达 BB 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
输入格式
一行四个正整数,分别表示 BB 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
输入输出样例
6 6 3 3
6
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 long long f[25][25]; 6 bool b[25][25]; 7 int main() 8 { 9 int x,y,xm,ym,i,j; 10 cin>>x>>y>>xm>>ym; 11 x+=2; 12 y+=2; 13 xm+=2; 14 ym+=2; 15 f[2][2]=1; 16 for(int i=1;i<=x;i++) 17 for(int j=1;j<=y;j++) 18 b[i][j]=true; 19 b[xm][ym]=false; 20 b[xm-1][ym-2]=false; 21 b[xm-2][ym-1]=false; 22 b[xm-2][ym+1]=false; 23 b[xm-1][ym+2]=false; 24 b[xm+1][ym+2]=false; 25 b[xm+2][ym+1]=false; 26 b[xm+1][ym-2]=false; 27 b[xm+2][ym-1]=false; 28 for(int i=2; i<=x; i++) //i是纵坐标y;j是横坐标x; 29 for(int j=2; j<=y; j++) 30 { 31 if(b[i][j]==false) continue; 32 f[i][j]=max(f[i-1][j]+f[i][j-1],f[i][j]); 33 } 34 cout<<f[x][y]; 35 return 0; 36 }
基本思路:f [ i ] [ j ] = f [ i - 1 ] [ j ] + f [ i ] [ j - 1 ] 也就是说 到达某一个点的路径数 等于 到达它上面的路径数 加 到达它左面的路径数
边界:f [1][1]=1
但注意,状态转移方程不能这么写, 必须用max比较,否则 f [1][1]会被覆盖成0;
例五:汉诺塔问题(递推 / 递归)
例六:放苹果(递推 / 搜索)
例七:判断整除
例八:踩方格
补充:当递推遇见高精度
数楼梯
题目描述
楼梯有 NN 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
输入格式
一个数字,楼梯数。
输出格式
输出走的方式总数。
输入输出样例
4
5
说明/提示
- 对于 60\%60% 的数据,N \leq 50N≤50;
- 对于 100\%100% 的数据,N \leq 5000N≤5000。
1 #include<iostream> 2 using namespace std; 3 int n,f[5010][5010],len; 4 void jiafa(int k) 5 { 6 for(int i=1; i<=len; i++) 7 f[k][i]=f[k-1][i]+f[k-2][i]; 8 for(int i=1; i<=len; i++) 9 if(f[k][i]>=10) 10 { 11 f[k][i+1]+=f[k][i]/10; 12 f[k][i]%=10; 13 if(f[k][len+1]>0)len++; 14 } 15 } 16 int main() 17 { 18 cin>>n; 19 len=1; 20 f[1][1]=1;//预处理 21 f[2][1]=2;//预处理 22 for(int i=3; i<=n; i++)//开始计算 23 jiafa(i); 24 for(int i=len; i>=1; i--)//输出 25 cout<<f[n][i]; 26 return 0; 27 }
思路:f [ i ] [ j ] 表示斐波那契数列第 i 项的第 j 位 (如 f [4][1]表示 f [4]的第1位数即为5)
(4.6日再写)
五种典型的递推关系:
1.斐波那契数列:
2.Hanoi塔问题:
3.平面分割问题:
4.卡特兰数:
5.第二类 Stirling 数:




