人工智能概率统计基础——似然函数及其与的交叉熵关系

似然函数（Likelihood Function）

似然函数是概率统计中的一个核心概念，用于衡量参数 θ 给定时，观察到数据的可能性。换句话说，似然函数表示已知数据后，模型参数的可能性。

1. 定义

对于一组观测数据 {x₁,x₂,…,x_n}，假设数据由某个概率分布 P(x;θ)生成，其中 θ 是分布的参数。那么似然函数定义为：

L(θ)=P(x1,x2,…,xn;θ)

即：似然函数是给定参数 θ 时，观测到这组数据的联合概率。

2. 与概率密度的关系

虽然似然函数和概率密度函数 P(x;θ)看似相同，但它们的解释是不同的：

• 概率密度函数：
  • 给定参数 θ，描述数据的概率分布。
  • 参数固定，数据是变量。
• 似然函数：
  • 给定数据，描述参数 θ 的可能性。
  • 数据固定，参数是变量。

3. 表达式形式

3.1 离散型数据

对于离散型数据，似然函数是概率的乘积：

3.2 连续型数据

对于连续型数据，似然函数是概率密度的乘积：

 其中 f(x_i;θ)是概率密度函数。

3.3 对数似然函数

为了方便优化和数值稳定性，通常取对数得到对数似然函数：

 

4. 最大似然估计（MLE）

似然函数的主要用途是最大似然估计（Maximum Likelihood Estimation, MLE），即找到使似然函数最大的参数值 θ：

或等价于：

 

这里最大化对数似然是因为：

1. 对数将乘积转换为求和，简化计算。
2. 数值计算更稳定。

 

5. 示例

5.1 离散数据

假设有 nnn 次抛硬币实验，观测结果为 x1,x2,…,xn∈{0,1}，概率为：

P(x_i​=1;p)=p,P(x_i​=0;p)=1−p

似然函数表示所有 nnn 次实验的联合概率： 

取对数： 

 最大化对数似然可以求得最优参数：

 

5.2 连续数据

假设有 n 个样本来自正态分布 N(μ,σ2)，其概率密度函数为：

似然函数为： 

 对数似然函数为：

 通过对 μ 和 σ2求导，可以求得最大似然估计：

 

6. 应用场景

1. 参数估计：

   • 最大似然估计（MLE）是统计建模中最常用的参数估计方法。
   • 如线性回归、逻辑回归等模型中使用 MLE 来估计模型参数。

2. 机器学习模型训练：

   • 损失函数与似然函数直接相关。例如：
     • 逻辑回归中的交叉熵损失是负对数似然。
     • 高斯混合模型（GMM）通过最大化似然训练。

3. 假设检验：

   • 比较不同模型的对数似然值以选择最优模型（如 AIC、BIC）。

4. 贝叶斯方法：

   • 在贝叶斯推断中，似然函数是后验概率计算的重要部分。

 

简单的似然函数计算例子

假设我们要对一个硬币的正面朝上的概率 p 进行估计，基于抛硬币实验的观测数据计算似然函数，并找到最优的参数值 p。

1. 问题描述

假设我们进行了 10 次抛硬币实验，结果如下：x=[1,0,1,1,0,1,0,1,1,0]

• 其中 1 表示正面朝上，0 表示反面朝上。
• 我们的目标是估计 p（硬币正面朝上的概率）。

2. 似然函数

每次实验的概率可以用伯努利分布表示：

 

似然函数表示所有观测结果的联合概率：

 展开为：

 

在我们的数据中：

• 正面次数：x=1 的个数是 6。
• 反面次数：x=0 的个数是 4。

因此，似然函数为：

L(p)=p^6⋅(1−p)⁴

3. 对数似然函数

为了简化计算，通常取对数似然：

logL(p)=6log(p)+4log(1−p)

4. 最大似然估计

通过最大化 log⁡L(p) 找到最优参数 p。

手工计算： 对 log⁡L(p) 求导，并令导数为 0：

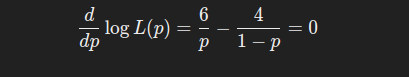
 解得：p = 6 / (6+4）=0.6

总结

• 似然函数：衡量给定参数时，观测数据的可能性。
• 对数似然函数：简化计算和优化的数学形式。
• 最大似然估计（MLE）：通过最大化似然函数找到最优参数。
• 应用：广泛用于统计学、机器学习、假设检验和贝叶斯推断中。

似然函数的核心在于将数据与模型参数联系起来，为参数估计和模型选择提供了基础。

 

 

---

 

交叉熵损失函数实际上是负对数似然函数（Negative Log-Likelihood, NLL）的一种形式，具体来说，它是逻辑回归模型的似然函数取对数并加负号后得到的。

交叉熵与似然函数的关系

在逻辑回归中：

模型输出的是类别 y的条件概率：

其中 σ(z_i)是 Sigmoid 函数。

目标是通过最大化似然函数，使得模型参数 θ 能够最好地拟合数据。

1. 似然函数

似然函数定义为所有样本的联合概率：

 对每个样本的概率，分类问题可以表示为：

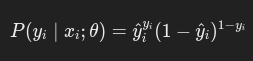
于是似然函数为：

 

2. 对数似然函数

取对数得到对数似然函数（Log-Likelihood, LL）：

 

3. 损失函数（交叉熵）

在模型训练中，我们最小化的是负对数似然：

 

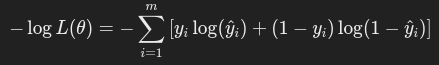
将负对数似然取平均，就得到了交叉熵损失函数：

 

总结

• 交叉熵损失函数 是负对数似然的平均形式。
• 在逻辑回归和分类问题中，最大化似然函数等价于最小化交叉熵损失。
• 交叉熵损失用于衡量预测的分布（y^​）与实际分布（y）之间的差异。