人工智能之机器学习最优化基础——凸优化

凸优化（Convex Optimization） 是优化问题的一个重要分支，其目标是最小化或最大化一个凸函数（或凹函数），通常受限于一组凸约束条件。由于凸优化问题具有良好的数学性质，许多优化问题可以转化为凸优化问题并高效求解。

 

1. 什么是凸优化问题？

一个标准的凸优化问题可以表示为：

 

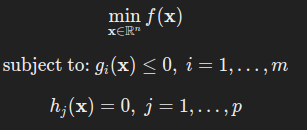
定义中的组成部分：

1. 目标函数 f(x)：

   • 是一个凸函数（若最大化，则是凹函数）。

2. 不等式约束 g_i(x)≤0：

   • 每个 g_i(x)是一个凸函数。

3. 等式约束 h_j(x)=0：

   • 每个 h_j(x)是一个仿射函数（线性或恒定的函数）。

凸函数的定义：

• 函数 f(x)f(\mathbf{x})f(x) 在定义域 CCC 上是凸的，当且仅当：

　　　　f(λx_1​+(1−λ)x₂​)  ≤  λf(x_1​)+(1−λ)f(x₂​),  ∀x₁​,x₂∈C  ,  λ∈[0,1].

直观地，凸函数的图像是一个“开口向上的碗”。

凸集合的定义：

• 集合 C 是凸的，当且仅当：λx₁​+(1−λ)x₂​∈C,  ∀x₁​,x₂​∈C,  λ∈[0,1].

2. 凸优化的性质

(1) 全局最优性

• 如果 f(x)是凸函数，且 C 是凸集合，那么任何局部最优解都是全局最优解。
• 优化问题的良好性质使得凸优化问题易于求解。

(2) 强对偶性

• 在凸优化中，原问题与其对偶问题之间通常具有强对偶性（Slater 条件满足时成立），即：

　　　　原问题的最优值=对偶问题的最优值.

(3) 凸性的传递

• 凸函数的非负加权和仍然是凸的。
• 若 g(f(x))中 f(x)是凸函数，且 g 是单调递增凸函数，则组合函数也是凸的。

3. 凸优化的应用

凸优化被广泛应用于以下领域：

1. 机器学习：
   • 支持向量机（SVM）：优化凸二次规划问题。
   • 正则化回归（如岭回归、Lasso）：目标函数是凸的。
2. 信号处理：
   • 滤波器设计、信号重建。
3. 控制理论：
   • 最优控制问题中的线性二次调节器（LQR）。
4. 金融：
   • 投资组合优化（如均值-方差优化）。
5. 运筹学：
   • 线性规划（Linear Programming，LP）和二次规划（Quadratic Programming，QP）。
6. 图像处理：
   • 图像去噪、图像分割问题。

4. 常见的凸优化问题

(1) 线性规划（Linear Programming, LP）

目标：

 约束：A_x≤b,x≥0

f(x)=c^Tx是线性函数，属于凸函数。

应用：资源分配问题、供应链管理。

(2) 二次规划（Quadratic Programming, QP）

目标：

 

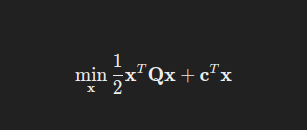
 约束：A_x≤b

若 Q是半正定矩阵，则目标函数是凸的。

 

(3) 二次锥规划（Second-Order Cone Programming, SOCP）

目标和约束形式可以包含二次锥约束，例如：

∥Ax+b∥2​≤c^Tx+d

应用：天线设计、金融风险控制。

(4) 半定规划（Semidefinite Programming, SDP）

目标：

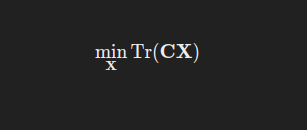
 约束：X⪰0,Tr(A_i​X)=b_i

应用：矩阵优化问题、系统稳定性分析。

5. 求解凸优化问题的方法

(1) 梯度下降法（Gradient Descent）

• 适合无约束凸优化问题。
• 更新规则：x_k+1​=x_k​−η∇f(x_k​)   

其中 η 是学习率。

(2) 牛顿法（Newton's Method）

• 利用二阶导数（Hessian 矩阵）加速收敛。
• 更新规则：x_k+1​=x_k​−∇²f(x_k​)⁻¹∇f(x_k​)
• 缺点：计算开销较大。

(3) 内点法（Interior-Point Method）

• 适合线性规划和二次规划等带约束的凸优化问题。
• 思路：通过松弛变量将约束嵌入目标函数。

(4) 对偶方法（Dual Methods）

• 利用强对偶性，将原问题转化为更易求解的对偶问题。

(5) 投影梯度法

• 适用于有约束的凸优化问题。
• 每次更新后将解投影到约束集内。

6. 凸优化的优缺点

优点：

1. 全局最优性：凸优化问题不存在局部最优解，任何局部最优解即为全局最优解。
2. 求解高效：许多凸优化问题有高效的数值解法。
3. 理论完善：凸优化具有丰富的数学理论支持。

缺点：

1. 问题建模难度：需要将非凸问题转化为凸问题，建模复杂。
2. 适用范围有限：某些优化问题（如深度学习中的非凸优化）无法直接应用。

总结

凸优化是一类特殊的优化问题，具有良好的理论性质和求解效率。其广泛应用于机器学习、信号处理、控制理论等领域。尽管凸优化问题的范围有限，但通过巧妙的建模和问题转化，许多实际问题可以利用凸优化技术高效求解。

​