人工智能之机器学习线代基础——核空间（Kernel Space）

在矩阵的上下文中，ker⁡(A) 是矩阵 A 的核空间（Kernel Space），也称为零空间（Null Space），它表示在矩阵 A 的线性变换下被映射到零向量的所有输入向量的集合。

1. 核空间的定义

对于一个矩阵 A∈R^m×n，核空间 ker⁡(A)定义为：

ker(A)={x∈Rⁿ:Ax=0}

核空间的性质：

1. ker⁡(A) 是一个向量空间。
2. 核空间的维数称为矩阵 A的零空间维数（nullity）。

2. 核空间与秩的关系

根据线性代数中的秩-零化维数定理（Rank-Nullity Theorem），矩阵的秩 rank(A)和核空间维数 nullity(A)满足以下关系：

rank(A)+nullity(A)=n

其中：

• n 是矩阵 A 的列数；
• rank(A)：矩阵的秩，列空间的维数；
• nullity(A)：核空间的维数。

因此：

nullity(A)=n−rank(A)

 

3. 核空间与特征值的关系

特征值为零时，对应的特征向量构成矩阵的核空间：

• 若矩阵 A 的特征值 λ=0，说明存在非零向量 x 使 Ax=0，即 x∈ker⁡(A)。
• 核空间的维数等于零特征值的重数。

　　公式化关系

　　若 A 是一个 n×n的矩阵，秩和核空间维数满足：

　　rank(A)=n−dim⁡(ker⁡(A))=n−(零特征值的个数).

 

4. 核空间的几何意义

在几何上，ker⁡(A) 表示：

1. 被线性变换 A 压缩到零向量的输入向量的集合。
2. ker⁡(A)是矩阵 A 的列向量无法覆盖的空间。
3. 核空间的维数表示线性变换 A 的退化程度。

5. 核空间的计算方法

步骤

1. 写出矩阵方程 Ax=0。
2. 对矩阵 A 进行行简化，化为简化行阶梯形矩阵（RREF）。
3. 求解线性方程组，得到自由变量。
4. 自由变量的解构成核空间的基。

示例

　　计算矩阵

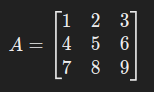
 的核空间。

(1) 化为增广矩阵：

 (2) 化为行阶梯形矩阵： 通过初等行变换：

 

 

(3) 解线性方程组： 根据方程：

x₁+2x₂+3x₃=0  x₂+2x₃=0

取自由变量 x₃=t，解得：

x₂=−2t,x₁=t

核空间的基为：

 

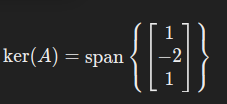
6. 核空间的实际应用

6.1 线性方程组的解

• 核空间是齐次方程组 Ax=0A\mathbf{x} = \mathbf{0}Ax=0 的解空间。
• 非齐次方程组的通解为特解加齐次解的组合。

6.2 判断矩阵的秩

• 核空间的维数直接决定了矩阵的秩： rank(A)+dim⁡(ker⁡(A))=n

6.3 特征值和特征向量分析

• 零特征值的存在与核空间直接相关，核空间维数等于零特征值的重数。

6.4 信号处理与数据分析

• 在主成分分析（PCA）中，核空间用于降维。
• 核空间分析可用于数据相关性的判断。

总结

ker⁡(A) 是描述线性变换的重要工具：

• 从几何上，核空间是矩阵映射为零的输入向量集合。
• 核空间的维数（nullity）与矩阵的秩（rank）密切相关，通过秩-零化维数定理联系。
• 在实际应用中，核空间用于解方程组、数据降维、信号处理等多个领域。

---

 

核空间可以理解为矩阵的解吗？

核空间（ker⁡(A)）与矩阵的解确实有密切关系，但两者并不完全等同。核空间是一个更广泛的概念，它描述了一个矩阵 A 在齐次线性方程 Ax=0中的所有解的集合。

核空间与“解”的联系

核空间是齐次线性方程组的解空间

对于齐次方程组 Ax=0，所有的解都在核空间内。因此可以说：

• 核空间完全描述了这个方程组的解。
• 如果矩阵 A 是 n×n的方阵：
• 若 ker⁡(A)={0}，即只有零向量是解，则 A 的秩为 n，矩阵满秩且可逆。
• 若 ker⁡(A)包含非零解，则 A 的秩小于 n，矩阵不可逆。

核空间与非齐次方程的解

对于非齐次方程 Ax=b，解的形式为：

x=x_p+x_h,

其中：

• x_p​：是方程 Ax=b的一个特解；
• x_h​：是对应齐次方程 Ax=0的解。

核空间（ker⁡(A)）描述了非齐次方程组所有解的增量部分，因为：

• 核空间的任何向量加到特解上，仍然是非齐次方程的解。

核空间的几何理解

从几何上看：

1. 核空间是矩阵 A 的线性变换将向量压缩到零的输入向量的集合。
2. 核空间的维数 nullity(A) 表示线性变换 A 的“退化程度”：
   • 如果 ker⁡(A)={0}，说明变换是满秩的，没有退化。
   • 如果 ker⁡(A) 包含非零向量，说明变换有退化，部分输入被压缩到零。

例如，对于二维平面上的矩阵：

• 如果矩阵将二维向量映射到一条直线上，则核空间是与该直线正交的方向。
• 如果矩阵将二维向量压缩到一个点（零向量），则核空间是整个二维空间。

核空间的性质

1. 核空间始终是矩阵所在域的一个子空间。

2. 核空间的维数通过秩-零化维数定理与矩阵的秩相关：

   rank(A)+nullity(A)=n,其中 n 是矩阵的列数。

3. 核空间的基（Basis）可以通过解线性方程组 Ax=0得到，基向量的个数等于核空间的维数。

示例：核空间与解的联系

齐次线性方程的例子

矩阵：

 

方程：

Ax=0.

步骤 1：化简 A将 A 化为简化行阶梯形矩阵：

 

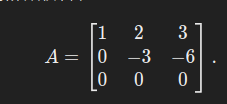
步骤 2：求解方程 对应的方程组为：

x₁+2x₂+3x₃=0, 

x₂ + 2x₃ = 0.

取 x₃=t，解得：

x₂=−2t,x₁=t.

核空间：

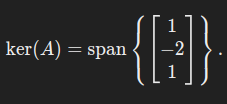
 这表示齐次方程 Ax=0 的解是：

 

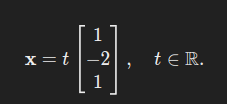
非齐次线性方程的例子

方程：

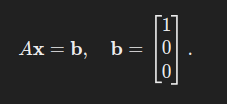
 通过计算特解（略），假设特解为：

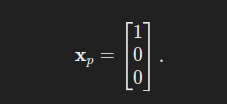
 非齐次方程的解为：

 

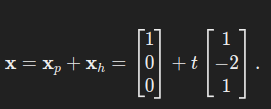
核空间描述了所有可能的增量 x_h。

 

核空间与“解”的区别与联系

• 核空间是解空间的一部分：

  • 核空间描述了所有齐次线性方程 Ax=0 的解。
  • 非齐次方程的解是特解加核空间中的解。

• 核空间是子空间：

  • 核空间是一个向量空间，具有基和维数的属性。
  • 单个解可能不是一个空间，而是向量空间中的一个元素。

总结

核空间可以理解为齐次线性方程组解的集合，但它本身不仅仅是“解”，而是一个具有线性代数结构的向量空间。对于非齐次线性方程，核空间提供了解的“增量部分”，通过特解和核空间的组合可以表示所有解。